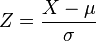1.- ESTADÍSTICA GENERAL: TEORÍA Y EJERCICIOS : MEDIA,MODA,MEDIANA,DESVIACION TIPICA, VARIANZA,,,,,,,,,,,,,, (C.F.G.S Y AU)
2.- PROBABILIDAD GENERAL........ (C.F.G.S Y AU)
EJERCICIOS DE PROBABILIDAD TOTAL I
El ego nos impide aprender y crecer
(Dalai Lama)
Distribución binomial o de Bernoulli
En muchas ocasiones cuando realizamos un experimento, observamos que los posibles resultados son dos sucesos contrarios y complementarios entre sí: hombre/mujer, correcto/incorrecto, enfermo/sano, etc. A este tipo de experimentos los llamaremos dicotómicos, denominando a los sucesos como "éxito" o "fracaso" y denotando sus probabilidades de la siguiente manera:
Éxito: Lo representamos por la letra A y su probabilidad es p = P(A)
Fracaso: Usamos la nomenclatura A para expresar el suceso contrario y su probabilidad es q = 1 - p = 1 - P(A)
Así, por ejemplo, el experimento de lanzar una moneda es una experiencia dicotómica, se puede obtener cara o cruz. Si llamamos al suceso A obtener cara,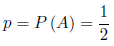 . Por tanto obtener cruz es
. Por tanto obtener cruz es 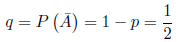 .
.
La distribución de probabilidad discreta que estudia este tipo de experimentos se llama distribución binomial, representada por B(n, p), donde:
n: Número de veces que se repite el experimento.
p: Es la probabilidad de éxito en cada experiencia p = P(A).
Estas distribuciones permiten calcular la probabilidad del número de éxitos, denotado por P (x=r), donde r sólo podrá tomar valores entre 0 y n.
Calcularemos la probabilidad P(x=r) de obtener r éxitos en una distribución binomial B(n, p) de la siguiente manera:
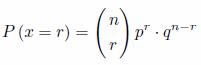
Y los parámetros de esta distribución son:
Media: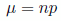 .
.
Desviación: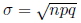 .
.


Distribución binomial o de Bernoulli
En muchas ocasiones cuando realizamos un experimento, observamos que los posibles resultados son dos sucesos contrarios y complementarios entre sí: hombre/mujer, correcto/incorrecto, enfermo/sano, etc. A este tipo de experimentos los llamaremos dicotómicos, denominando a los sucesos como "éxito" o "fracaso" y denotando sus probabilidades de la siguiente manera:
Éxito: Lo representamos por la letra A y su probabilidad es p = P(A)
Fracaso: Usamos la nomenclatura A para expresar el suceso contrario y su probabilidad es q = 1 - p = 1 - P(A)
Así, por ejemplo, el experimento de lanzar una moneda es una experiencia dicotómica, se puede obtener cara o cruz. Si llamamos al suceso A obtener cara,
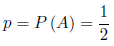 . Por tanto obtener cruz es
. Por tanto obtener cruz es 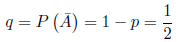 .
.La distribución de probabilidad discreta que estudia este tipo de experimentos se llama distribución binomial, representada por B(n, p), donde:
n: Número de veces que se repite el experimento.
p: Es la probabilidad de éxito en cada experiencia p = P(A).
Estas distribuciones permiten calcular la probabilidad del número de éxitos, denotado por P (x=r), donde r sólo podrá tomar valores entre 0 y n.
Calcularemos la probabilidad P(x=r) de obtener r éxitos en una distribución binomial B(n, p) de la siguiente manera:
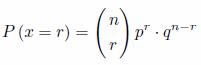
Y los parámetros de esta distribución son:
Media:
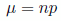 .
.Desviación:
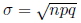 .
.Distribución binomial que se aproxima a la normal
Hemos estudiado distribuciones de probabilidad de variables discretas y continuas, pero esa diferencia no es estricta, puesto que una variable continua se puede discretizar debido a limitaciones con instrumentos de medida. También, cuando tenemos un número elevado de mediciones discretas se pueden agrupar en intervalos y las estudiamos como continuas. Como ves, hay una gran relación entre ambas, así que no es descabellado afirmar que una distribución binomial B(n,p) pueda aproximarse a una distribución normal N(μ,σ).
Recordemos la fórmula de una binomial: 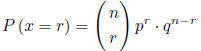 , siendo μ = n·p y
, siendo μ = n·p y 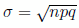 .
.
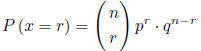 , siendo μ = n·p y
, siendo μ = n·p y 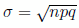 .
.
El problema reside en que cuando n es muy grande resulta engorroso realizar los cálculos del número combinatorio y las potencias. Ese inconveniente lo resolvió el matemático francés Abraham de Moivre (1667 - 1754), que demostró que bajo ciertas condiciones la distribución binomial B(n,p) se puede aproximar a una distribución normal 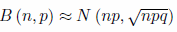 Posteriormente se podría aproximar a la normal N(0,1) por tipificación de la variable.
Posteriormente se podría aproximar a la normal N(0,1) por tipificación de la variable.
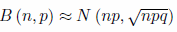 Posteriormente se podría aproximar a la normal N(0,1) por tipificación de la variable.
Posteriormente se podría aproximar a la normal N(0,1) por tipificación de la variable.
El error por aproximación se reduce a medida que n aumenta. Para comprobarlo basta verificar que np ≥ 5 y nq ≥ 5, según las condiciones de Moivre.

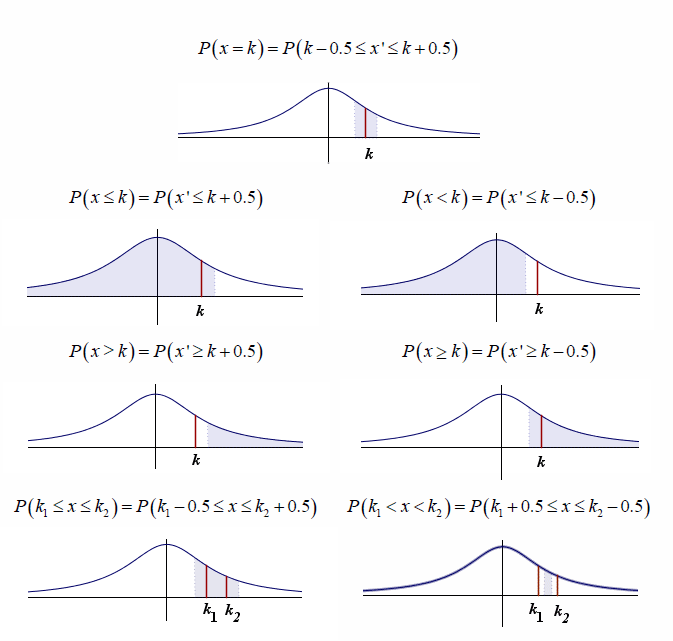
Corrección de continuidad o de Yates
Cuando aproximamos una distribución binomial a una distribución normal, tomamos una variable discreta 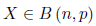 y la aproximamos a una variable continua
y la aproximamos a una variable continua 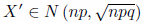 , cometiéndose un error que podemos solventar con la corrección de continuidad o corrección de Yates.
, cometiéndose un error que podemos solventar con la corrección de continuidad o corrección de Yates.
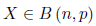 y la aproximamos a una variable continua
y la aproximamos a una variable continua 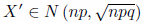 , cometiéndose un error que podemos solventar con la corrección de continuidad o corrección de Yates.
, cometiéndose un error que podemos solventar con la corrección de continuidad o corrección de Yates.
La corrección de continuidad la realizamos de la siguiente manera:


Distribución normal
En estadística y probabilidad se llama distribución normal, distribución de Gauss o distribución gaussiana, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece aproximada en fenómenos reales [cita requerida].
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La importancia de esta distribución radica en que permite modelarnumerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.
De hecho, la estadística descriptiva sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.
La distribución normal también es importante por su relación con la estimación por mínimos cuadrados, uno de los métodos de estimación más simples y antiguos.
Algunos ejemplos de variables asociadas a fenómenos naturales que siguen el modelo de la normal son:
- caracteres morfológicos de individuos como la estatura;
- caracteres fisiológicos como el efecto de un fármaco;
- caracteres sociológicos como el consumo de cierto producto por un mismo grupo de individuos;
- caracteres psicológicos como el cociente intelectual;
- nivel de ruido en telecomunicaciones;
- errores cometidos al medir ciertas magnitudes;
- etc.
Historia[editar]
La distribución normal fue presentada por primera vez por Abraham de Moivre en un artículo del año 1733, que fue reimpreso en la segunda edición de su The Doctrine of Chances, de 1738, en el contexto de cierta aproximación de la distribución binomial para grandes valores de n. Su resultado fue ampliado por Laplace en su libro Teoría analítica de las probabilidades (1812), y en la actualidad se llama Teorema de De Moivre-Laplace.
Laplace usó la distribución normal en el análisis de errores de experimentos. El importantemétodo de mínimos cuadrados fue introducido por Legendre en 1805. Gauss, que afirmaba haber usado el método desde 1794, lo justificó rigurosamente en 1809 asumiendo una distribución normal de los errores. El nombre de Gauss se ha asociado a esta distribución porque la usó con profusión cuando analizaba datos astronómicos y algunos autores le atribuyen un descubrimiento independiente del de De Moivre. Esta atribución del nombre de la distribución a una persona distinta de su primer descubridor es un claro ejemplo de la Ley de Stigler.
El nombre de "campana" viene de Esprit Jouffret que usó el término "bell surface" (superficie campana) por primera vez en 1872 para una distribución normal bivariante de componentes independientes. El nombre de "distribución normal" fue otorgado independientemente porCharles S. Peirce, Francis Galton y Wilhelm Lexis hacia 1875.
Propiedades[editar]
Algunas propiedades de la distribución normal son:
- Es simétrica respecto de su media, μ;
- La moda y la mediana son ambas iguales a la media, μ;
- Los puntos de inflexión de la curva se dan para x = μ − σ y x =μ + σ.
- Distribución de probabilidad en un entorno de la media:
- en el intervalo [μ - σ, μ + σ] se encuentra comprendida, aproximadamente, el 68,26% de la distribución;
- en el intervalo [μ - 2σ, μ + 2σ] se encuentra, aproximadamente, el 95,44% de la distribución;
- por su parte, en el intervalo [μ -3σ, μ + 3σ] se encuentra comprendida, aproximadamente, el 99,74% de la distribución. Estas propiedades son de gran utilidad para el establecimiento de intervalos de confianza. Por otra parte, el hecho de que prácticamente la totalidad de la distribución se encuentre a tres desviaciones típicas de la media justifica los límites de las tablas empleadas habitualmente en la normal estándar.
Estandarización de variables aleatorias normales[editar]
Como consecuencia de la Propiedad 1; es posible relacionar todas las variables aleatorias normales con la distribución normal estándar.
Si  ~
~  , entonces
, entonces
 ~
~  , entonces
, entonces
es una variable aleatoria normal estándar:  ~
~  .
.
 ~
~  .
.
La transformación de una distribución X ~ N(μ, σ) en una N(0, 1) se llama normalización, estandarización o tipificación de la variable X.
EJERCICIO INTERESANTE DE DISTRIBUCION NORMAL
La desviación típica es la raíz cuadrada de la varianza
YOUTUBES PARA EL USO DE LA CALCULADORA FX 570ES PLUS
A) NUMERO FACTORIAL EN LA CALCULADORA
PROBABILIDAD DE SUCESOS INDEPENDIENTES
PROBABILIDAD TOTAL: DIAGRAMA DE ARBOL
TEOREMA DE BAYES: 2º BACHILLERATO
DISTRIBUCION NORMAL
A) NUMERO FACTORIAL EN LA CALCULADORA
PROBABILIDAD DE SUCESOS INDEPENDIENTES
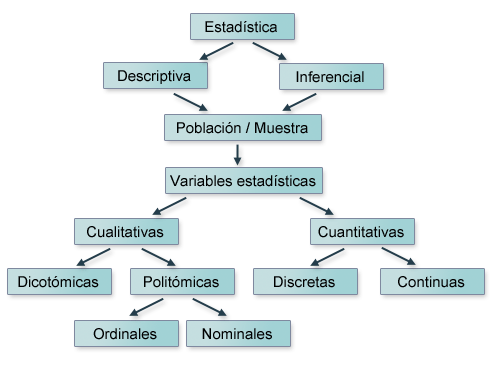
La estadística es la rama de las matemáticas que estudia la recolección, el análisis y la interpretación de datos. Términos usados habitualmente, como "media", "moda" o "desviación", tienen mucho que ver con la estadística.
Se puede dividir en dos grandes partes: la estadística descriptiva, que se encarga de la recolección y visualización de conjuntos de datos; y la estadística inferencial, con la que se pueden hacer modelos de estos datos y establecer conclusiones y predicciones.
Se utiliza en muchísimas áreas de la ciencia y la humanística, pero hay dos lugares de aplicación fundamental: la economía y la política. De hecho, el término estadística procede del término alemán "Ciencia del Estado". Es decir, se creó para analizar los datos que el estado recolectaba, a fin de poder valorar la situación del país y tomar decisiones en base a los resultados del análisis. Fue a partir del siglo XX cuando la estadística verdaderamente empezó a entrar en amplios campos de la vida cotidiana: salud pública, evolución de la economía, empleo, juegos de azar, medio ambiente...

Precisamente por su enorme interés económico, social e incluso político, la estadística puede ser también una herramienta que, mal utilizada, puede dar lugar a confusiones, engaños o incluso manipulaciones. A menudo, empresas y gobiernos utilizan técnicas estadísticas cuestionables que dan lugar a resultados sesgados e interesados. Un conocimiento básico de esta disciplina nos permite identificar los estudios imparciales y objetivos, y rechazar los que han sido distorsionados con fines particulares.
Imaginemos que estamos lanzando una moneda al aire, que se supone que no está trucada y que por tanto el resultado es completamente aleatorio (es decir, al azar). Imaginemos que salen 9 veces seguidas cara. ¿Diríamos que en el siguiente lanzamiento hay más probabilidades de que ya salga cruz, o que hay tantas probabilidades como en la primera tirada?. El cálculo de probabilidades nos dirá que no importa las veces que haya salido cara en las tiradas anteriores: cada vez que tiremos la moneda, hay un 50% de probabilidades de que vuelva a salir cara. Y también nos dice que, en una sucesión de 50 tiradas de la moneda, es exactamente igual de probable que salga siempre cara respecto a que salga primero cara, luego cruz, luego cara y así hasta la última tirada.
En definitiva, la probabilidad se ocupa de estudiar la frecuencia con la que ocurren determinados eventos en situaciones en los que interviene el azar. Nos permite validar o refutar determinadas conclusiones que a menudo formulamos con nuestro sentido común (al pensar cosas como "hay más probabilidades de que ocurra esto" o "es muy difícil que pase esto otro"), y que puede ser de mucha utilidad, por ejemplo, en los juegos de azar o al asumir riesgos.
También se suele emplear la probabilidad cuando se estudian fenómenos de gran complejidad como el movimiento de los gases: determinar exactamente su comportamiento futuro implica unos cálculos tan costosos que se predice su comportamiento en base a probabilidades. Esto puede verse en las predicciones climatológicas de los informativos.
A pesar de su utilidad, las fórmulas asociadas a su estudio se desarrollaron hace poco tiempo, en comparación con otras ramas matemáticas. Fue en el siglo XVIII cuando Pierre-Simon Laplace hizo el primer intento para deducir una regla para la combinación de observaciones a partir de los principios de la teoría de las probabilidades, y en 1930 Andréi Kolmogorov desarrolló la base axiomática de la probabilidad utilizando teoría de la medida. Se puede decir, por tanto, que el estudio científico de la probabilidad es un desarrollo matemático reciente.
Sucesos compatibles e incompatibles
Espacio muestral. Sucesos
Vamos a definir algunos conceptos básicos necesarios para familiarizarnos con la terminología:
- Experimento aleatorio: Son aquellos experimentos que al repetirse en varias ocasiones con igualdad de condiciones pueden presentar diferentes resultados. Están relacionados con el azar, llamados experimentos, fenómenos o sucesos aleatorios.
- Espacio muestral: Llamaremos espacio muestral al conjunto de todos los resultados posibles, lo denotamos por E.
- Suceso: Llamaremos suceso a cualquier subconjunto del espacio muestral, a los sucesos los representamos con letras mayúsculas.
Tipos de sucesos
Existen diferentes tipos de sucesos:
- Sucesos elementales: También llamados sucesos simples. Son aquellos que están formados por un solo elemento del espacio muestral, o lo que es lo mismo, un único resultado del experimento aleatorio. En el experimento "Lanzar un dado", los sucesos elementales son: {1}, {2}, {3}, {4}, {5}, {6}, ya que solo puede salir un valor en cada tirada.
- Sucesos compuestos: Llamamos sucesos compuestos a los formados por dos o más sucesos elementales. En el experimento "Lanzar un dado", un ejemplo de suceso compuesto es: Obtener un número par = {2, 4, 6}.
- Suceso seguro: Es el suceso que siempre ocurre y que coincide con el espacio muestral E. En el experimento "Lanzar un dado", un ejemplo de suceso seguro es: Obtener cualquier número entero del 1 al 6.
- Suceso imposible: Es aquel suceso que no ocurre nunca, se representa por ɸ. En el experimento "Lanzar un dado", un ejemplo de suceso imposible es: Obtener un 10.
Operaciones con sucesos y propiedades
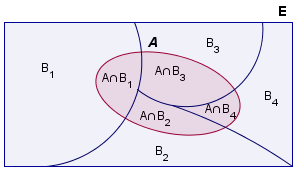
- Unión de sucesos: La unión de dos sucesos A y B, en un espacio muestral E, denotado por A∪B, es un nuevo suceso formado por todos los resultados que se encuentran en A, en B, o en ambos simultáneamente.
- Intersección de sucesos: La intersección de dos sucesos A y B, en un espacio muestral E, denotado por A∩B, es un nuevo suceso formado por todos los resultados que se encuentran en A y en B simultáneamente.
- Sucesos contrarios: El suceso contrario al suceso A, denotado por A en un espacio muestral E, es aquel que está formado por todos los sucesos elementales que se encuentran en el espacio muestral y no están en A. También llamado complemento de A.
- Diferencia de sucesos: Llamaremos diferencia entre dos sucesos A y B en un espacio muestral E, denotado por A-B, a un nuevo suceso formado por todos los resultados que se encuentran en A pero no en B. También podemos definirlo como la intersección del primer suceso con el contrario del segundo A-B = A∩B
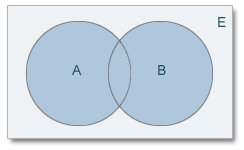
A ∪ B
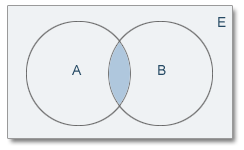
A ∩ B

A
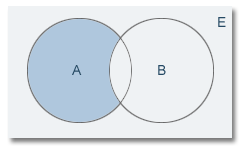
A - B
Sucesos compatibles e incompatibles
Decimos que dos o más sucesos son compatibles si comparten algún resultado en común. Por ejemplo, al lanzar un dado el suceso "obtener número primo" y "obtener número par" son compatibles, ya que el "2" pertenece a ambos. En caso contrario diremos que los sucesos son incompatibles.
Además se verifica lo siguiente:
- Si A ∩ B = ɸ entonces A y B son incompatibles.
- Si A ∩ B ≠ ɸ entonces A y B son compatibles.
Por tanto un suceso y su contrario son incompatibles.
Diagramas de Árbol
En algunas ocasiones para entender el experimento a estudiar, y determinar claramente el espacio muestral E, podemos utilizar un diagrama de árbol poniendo en cada rama cada una de las posibilidades.
EJERCICIOS

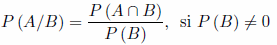
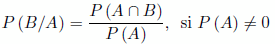
EJERCICIOS
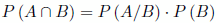
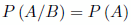
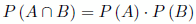
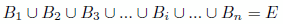
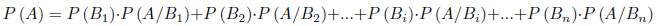
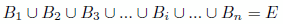
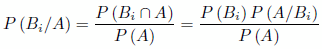
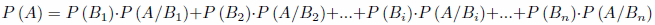
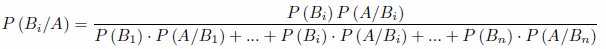
EJERCICIOS
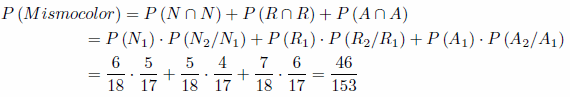
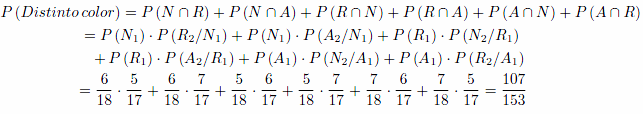
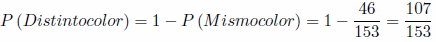
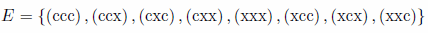
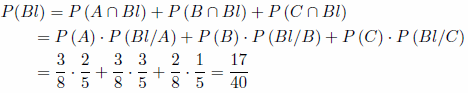
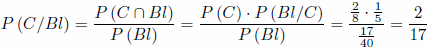
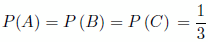
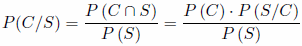
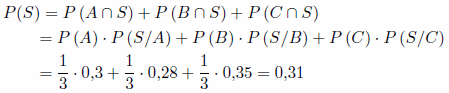
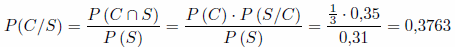
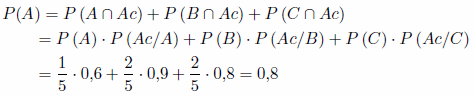
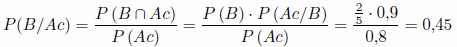
DISTRIBUCIÓN DISCRETA: DISTRIBUCIÓN BINOMIAL
EJERCICIOS
Probabilidad y propiedades
Como ya hemos visto, un suceso aleatorio A es aquel que depende del azar. Podemos estudiar este tipo de sucesos mediante la experimentación, por ejemplo lanzando un dado y anotando el número obtenido. El número de veces que se repite un resultado lo llamaremos frecuencia relativa fr (A)
Donde: 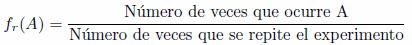
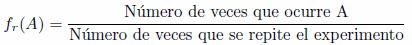
Cuando repetimos muchas veces el experimento, la frecuencia relativa suele tender a un número. A dicho valor lo llamaremos probabilidad de un suceso A, y lo expresamos como P(A).
Por tanto: 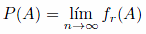
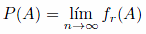
Regla de Laplace
Para calcular con exactitud la probabilidad de un suceso A, tendríamos que repetir el experimento un número de veces lo suficientemente grande. Para evitar esto, en experimentos que son equiprobables, es decir, que todos los sucesos elementales tienen la misma probabilidad (como lanzar un dado, extraer una carta de una baraja, etc), podemos calcular la probabilidad de que ocurra un suceso A utilizando la Ley de Laplace.

Propiedades de la probabilidad
Existe una serie de propiedades aplicadas a la probabilidad. Sean A y B dos sucesos elementales en un espacio muestral E, y P(A) y P(B) sus correspondientes probabilidades se cumple que:
- La probabilidad de un suceso seguro es:
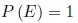
- La probabilidad de un suceso A está comprendido entre 0 y 1:
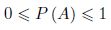
- La probabilidad de un suceso imposible es cero:
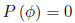
- La probabilidad del suceso contrario al suceso A es:
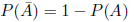
- La probabilidad de la unión de dos sucesos incompatibles es:
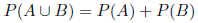 si
si 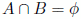
Podemos generalizar para n sucesos, incompatibles dos a dos, de la siguiente manera: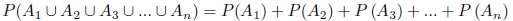
- La probabilidad de intersección de sucesos compatibles es:
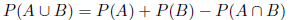 si
si 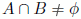
Podemos extender estas propiedades a más de dos sucesos que sean compatibles dos a dos. Por ejemplo, para el caso de tres sucesos: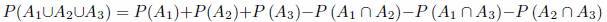
Probabilidad condicionada. Probabilidad total. Teorema de Bayes
En algunas ocasiones queremos realizar experimentos que constan de dos o más sucesos simples, como lanzar una moneda dos veces, lanzar 3 dados, extraer dos bolas de una urna, etc. A éste tipo de experiencias se les llama experiencias compuestas.
En el caso de experiencias compuestas como las extracciones, podemos distinguir claramente dos casos importantes:
- Extracciones con reemplazamiento: Son aquellas extracciones en las que después de cada extracción y observado su resultado, se devuelve el elemento donde estaba antes de la segunda extracción. De esta manera cada extracción tiene las mismas condiciones que la anterior.
- Extracciones sin reemplazamiento: Son aquellas extracciones en las que después de cada extracción y observado el resultado el objeto no se devuelve antes de la siguiente extracción. De esta manera las condiciones dependen de las extracciones anteriores.
Probabilidad condicionada
Diremos que dos sucesos son independientes si el resultado de una de ellas no depende del resultado de las demás, en caso contrario son sucesos dependientes.
Son sucesos independientes, lanzamiento de monedas, de dados o extracciones con reemplazamiento. Son sucesos dependientes todos aquellos que son extracciones sin reemplazamiento, o lanzar un dado y extraer una bola de una urna u otra dependiendo del número sacado en el dado.
En el caso de ser sucesos dependientes, tiene sentido de hablar de probabilidad condicionada.
Llamamos probabilidad del suceso A condicionado al suceso B, denotado de la siguiente manera 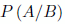 a:
a:
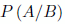 a:
a: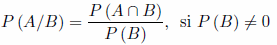
Análogamente probabilidad de un suceso B condicionado al suceso A,
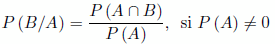
En ocasiones nos podremos ayudar de tablas de contingencia (tablas de doble entrada) para organizar mejor los datos.
EJERCICIOS
Probabilidad compuesta o de intersección de sucesos
Partiendo de la definición de probabilidad condicionada, podemos obtener la fórmula para la intersección de sucesos, llamada también probabilidad compuesta o probabilidad del producto para sucesos dependientes.
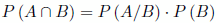
Si dos sucesos son independientes (el resultado de uno no modifica el resultado del otro) ocurre que:
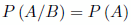
Por tanto:
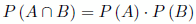
Tenemos entonces que:
- Si dos sucesos son dependientes:
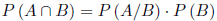
- Si dos sucesos son independientes:
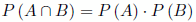
Probabilidad total
Si tenemos un suceso A, condicionado por otros sucesos Bi incompatibles dos a dos y de tal manera que:
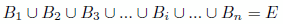
Tenemos entonces que la probabilidad del suceso A es igual a:
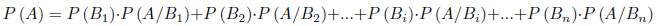

Teorema de Bayes
Bayes nos ayuda para calcular probabilidades a posteriori de diversas causas, una vez observado un suceso A.
Si tenemos varios sucesos Bi incompatibles dos a dos y de tal manera que:
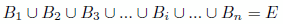
Tenemos por definición,
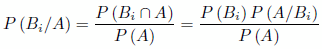
Si lo combinamos con la probabilidad total,
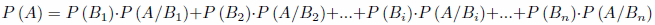
Obtenemos:
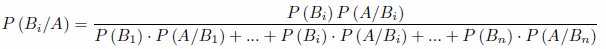
Ejemplo 1
Una compañía tiene dos proveedores A y B que le han suministrado artículos en mal estado en los últimos envíos. Los datos del último pedido vienen dados en la tabla:
| Buenos | Defectuosos | Total | |
| Proveedor A | 10 | 40 | 50 |
| Proveedor B | 20 | 130 | 150 |
| Total | 30 | 170 | 200 |
Calcular la probabilidad de que al elegir al azar un artículo:
a) Sea bueno.
b) Sea del proveedor A sabiendo que es defectuosa.
c) Sea del proveedor B y sea bueno.
d) Sea suministrado por el proveedor A o sea defectuoso.
b) Sea del proveedor A sabiendo que es defectuosa.
c) Sea del proveedor B y sea bueno.
d) Sea suministrado por el proveedor A o sea defectuoso.
Utilizaremos la tabla de contingencia, llamaremos a los sucesos:
- Bu: Sea bueno
- Df: Sea Defectuoso
- A: Ser del proveedor A
- B: ser del proveedor B
a) 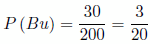
b)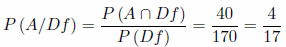
c)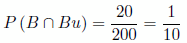
d)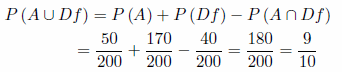
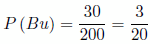
b)
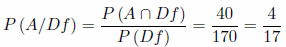
c)
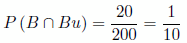
d)
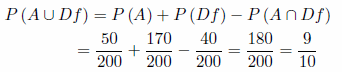
Ejemplo 2
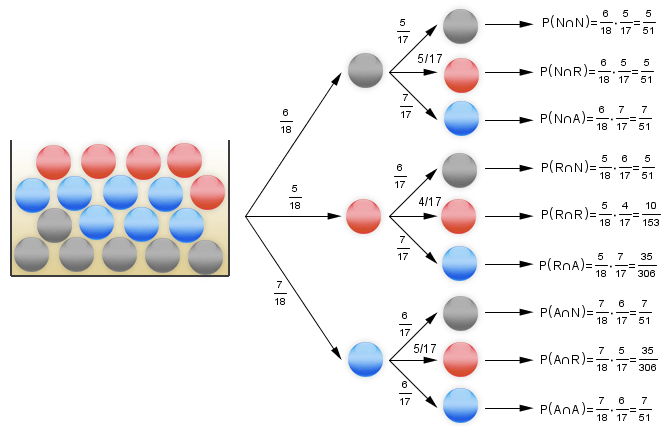
En una urna tenemos 6 bolas negras, 5 bolas rojas y 7 azules, el experimento consiste en extraer dos bolas. Hallar la probabilidad de que:
a) La primera bola sea roja y la segunda azul.
b) Se extraigan dos bolas del mismo color.
c) Dos bolas de diferente color.
b) Se extraigan dos bolas del mismo color.
c) Dos bolas de diferente color.
Realizamos el diagrama de árbol, sean los sucesos:
- N: Extraer una bola negra
- R: Extraer una bola roja
- A: Extraer una bola azul

a) 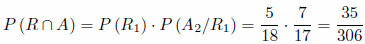
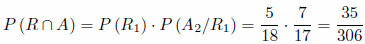
b) Extraer dos bolas del mismo color, es decir obtener dos bolas negras o dos bolas rojas o dos bolas azules.
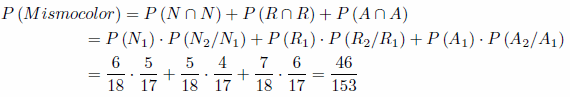
c) Extraer dos bolas de diferente color, (primera negra y segunda roja, primera negra y segunda azul, etc), por probabilidad total tenemos:
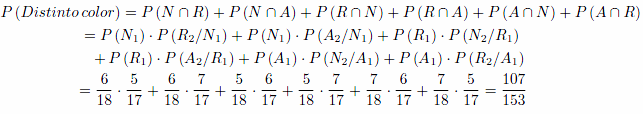
Observa que podemos obtenerla también de la siguiente manera:
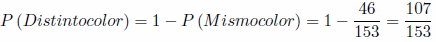
Ejemplo 3
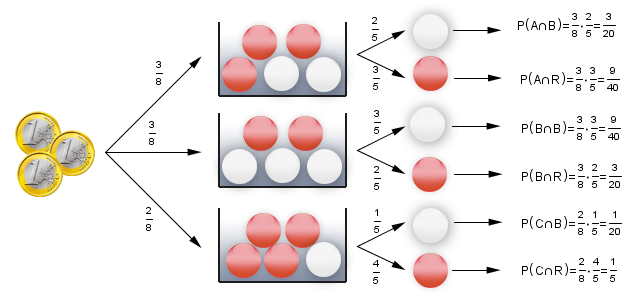
Se tienen tres bolsas A, B y C con el siguiente contenido: A contiene 2 bolas blancas y 3 bolas rojas; B tiene 3 bolas blancas y 2 bolas rojas; C tiene 1 bola blanca y 4 bolas rojas.
Se lanzan tres monedas y si se obtienen exactamente dos caras se extrae una bola de la bolsa A. Si se obtienen exactamente dos cruces, se extrae una bola de la bolsa B y en los restantes casos, se extrae una bola de la bolsa C. Se pide:
a) Probabilidad de que la bola extraída sea blanca.
b) Si la bola extraída es de color blanco ¿Cuál es la probabilidad de que haya sido extraída de la bolsa C?
Si lanzamos 3 monedas, veamos cual es su espacio muestral para determinar la probabilidad de obtener exactamente 2 caras. Sea:
- C: obtener cara
- X: Obtener cruz
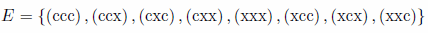
Escogemos la urna A si obtenemos exactamente 2 caras: 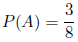
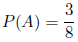
Escogemos la urna B si obtenemos exactamente 2 cruces: 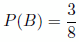
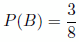
Escogemos la urna C el resto de los casos: 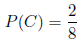
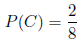

a) Utilizamos la fórmula de probabilidad total:
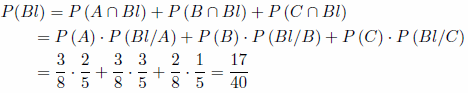
b) Utilizando el teorema de Bayes tenemos:
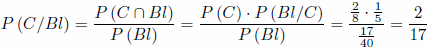
Ejemplo 4
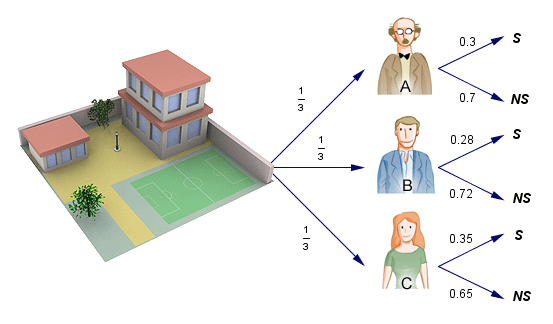
En un I.E.S. hay tres profesores de Física. Cuando un alumno se matricula en el centro tiene igual probabilidad de que le asignen uno u otro profesor de Física. La probabilidad de obtener como nota final un sobresaliente con el profesor A es 0.3; la de obtenerlo con el profesor B es de 0.28; y la de obtenerlo con el profesor C es 0.35.
Calcula la probabilidad de que, sabiendo que un alumno matriculado en Física ha obtenido sobresaliente, ¿cuál es la probabilidad de que le hubiesen asignado al profesor C?
Llamaremos:
- A, B, C: Que te asignen el profesor
- S: Obtener sobresaliente
- NS: No obtener sobresaliente
La probabilidad que te asignen un profesor u otra es la misma:
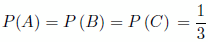

Nos piden P(C/S), por definición (Bayes):
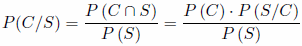
Por probabilidad total tenemos que:
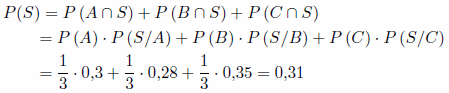
Sustituyendo en la fórmula de Bayes,
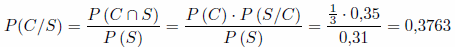
Ejemplo 5
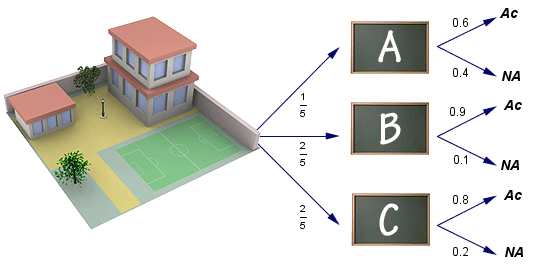
En una clase de Matemáticas de 50 alumnos se hacen tres grupos de trabajo, A, B y C, para preparar una batería de preguntas. En el grupo A hay 10 alumnos mientras que en el B y en el C hay 20 alumnos. La probabilidad de que un alumno del grupo A acierte una determinada pregunta es 0.6; un alumno del grupo B la acierta con una probabilidad de 0.9 y un alumno del grupo C la acierta con una probabilidad de 0.8. Elegido al azar un alumno de esa clase:
a) Calcula la probabilidad de que no acierte esa pregunta.
b) Si ha acertado esa pregunta, calcula la probabilidad de que sea del grupo B.
Llamaremos:
- A, B, C: Ser del grupo A, B o C respectivamente
- Ac: Acertar la pregunta
- NA: No Acertar la pregunta

a) 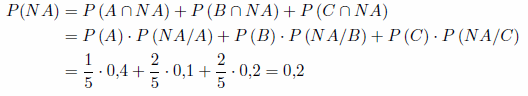
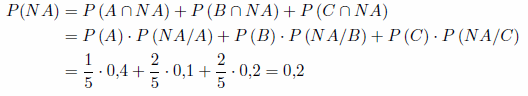
b) 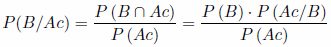
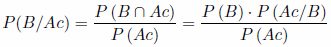
Por probabilidad total tenemos que:
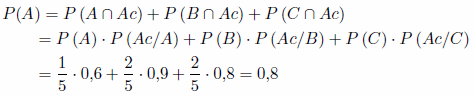
También podemos calcularla: 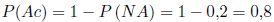
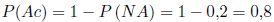
Sustituyendo en la fórmula de Bayes,
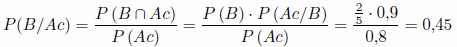
EJERCICIOS
DISTRIBUCION BINOMIAL




Ejercicio 3
resuelto

Ejercicio 4
resuelto


Ejercicio 5
resuelto




DISTRIBUCION BINOMIAL
Ejercicio 2 resuelto
Un agente de seguros
vende pólizas a cinco personas de la misma edad y que disfrutan de buena salud.
Según las tablas actuales, la probabilidad de que una persona en estas
condiciones viva 30 años o más es 2/3. Hállese la probabilidad de que,
transcurridos 30 años, vivan:
Soluciones:
1Las
cinco personas
B(5, 2/3) p = 2/3 q
= 1/3

2Al
menos tres personas

3Exactamente
dos personas

Ejercicio 3
resuelto
Si de seis a siete de la tarde se admite que un número de
teléfono de cada cinco está comunicando, ¿cuál es la probabilidad de que,
cuando se marquen 10 números de teléfono elegidos al azar, sólo comuniquen dos?
B(10, 1/5)p = 1/5q = 4/5

Ejercicio 4
resuelto
La probabilidad de que un hombre acierte en el blanco es
1/4. Si dispara 10 veces ¿cuál es la probabilidad de que acierte exactamente en
tres ocasiones? ¿Cuál es la probabilidad de que acierte por lo menos en una
ocasión?
B(10, 1/4) p
= 1/4q = 3/4


Ejercicio 5
resuelto
En una urna hay 30 bolas, 10 rojas y el resto blancas. Se
elige una bola al azar y se anota si es roja; el proceso se repite, devolviendo
la bola, 10 veces. Calcular la media y la desviación típica
B(10, 1/3) p
= 1/3q = 2/3
Ejercicio 1 resuelto
Se lanza una moneda
cuatro veces. Calcular la probabilidad de que salgan más caras que cruces (o
mas cruces que caras)
B(4, 0.5)
probabilidad de que salga
cara p = 0.5
probabilidad de que
salga cruz q = 0.5

Distribución binomial o de Bernoulli
Un
experimento sigue el modelo de la distribución binomial o de Bernoulli si:
1 En
cada prueba del experimento sólo son posibles dos resultados: el
suceso A (éxito) y su contrario .
.
2La probabilidad
del suceso A es constante, es decir, que no varía de una prueba a otra. Se
representa por p.
3El resultado obtenido
en cada prueba es independiente de los resultados obtenidos
anteriormente.
La distribución
binomial se suele representar por B(n, p).
n es el
número de pruebas de que
consta el experimento.
p es la
probabilidad de éxito.
La probabilidad de  es 1− p, y la representamos
por q.
es 1− p, y la representamos
por q.
Variable aleatoria binomial
La variable
aleatoria binomial, X, expresa el número de éxitos
obtenidos en cada prueba del experimento.
La variable
binomial es una variable aleatoria discreta, sólo puede tomar los valores
0, 1, 2, 3, 4, ..., n suponiendo que se han realizado n pruebas.
Ejemplo:
k = 6, al
lanzar una moneda 10 veces y obtener 6 caras.
DISTRIBUCIÓN DISCRETA: DISTRIBUCIÓN BINOMIAL