INTEGRALES. APLICACIONES


INTEGRALES. APLICACIONES
Integral Indefinida
El cálculo de integrales o cálculo integral es la operación inversa del cálculo de derivadas o cálculo diferencial.
El objetivo del cálculo integral es hallar todas las funciones cuya derivada sea una función dada f(x) o que su diferencial sea f(x) dx.
Por ejemplo: ¿cuál es la función cuya derivada es:…?
a) 2x b) 5x c) 3x2
d) x e) 4x3 f) 1
g) 4 h) cos x i) sen x
Definición de integral indefinida o función primitiva
Dada una función primitiva de f(x), se llama función primitiva de f(x) a una función F(x) cuya derivada sea f(x), esto es:

F (x) es primitiva de f (x) si F´(x) = f(x)
Por ejemplo: una función primitiva de 2x es la función x2, ya que la derivada de x2 es 2x (también serán funciones primitivas de 2x: x2+3;   x2+1/2;  x2-5;……
El conjunto de todas las funciones primitivas de f(x) se denomina integral indefinida de f(x) y se representa por:
.

Ejemplo: la integral indefinida de la función f(x)=2x es: (El calificativo de indefinida se debe a la aparición de la constante indeterminada C llamada constante de integración)
  1. Calcula la siguiente integral indefinida: teniendo en cuenta que: (tabla de integrales inmediatas: o  para y teniendo en cuenta que )


  1. Calcula las siguientes integrales:
a)



b)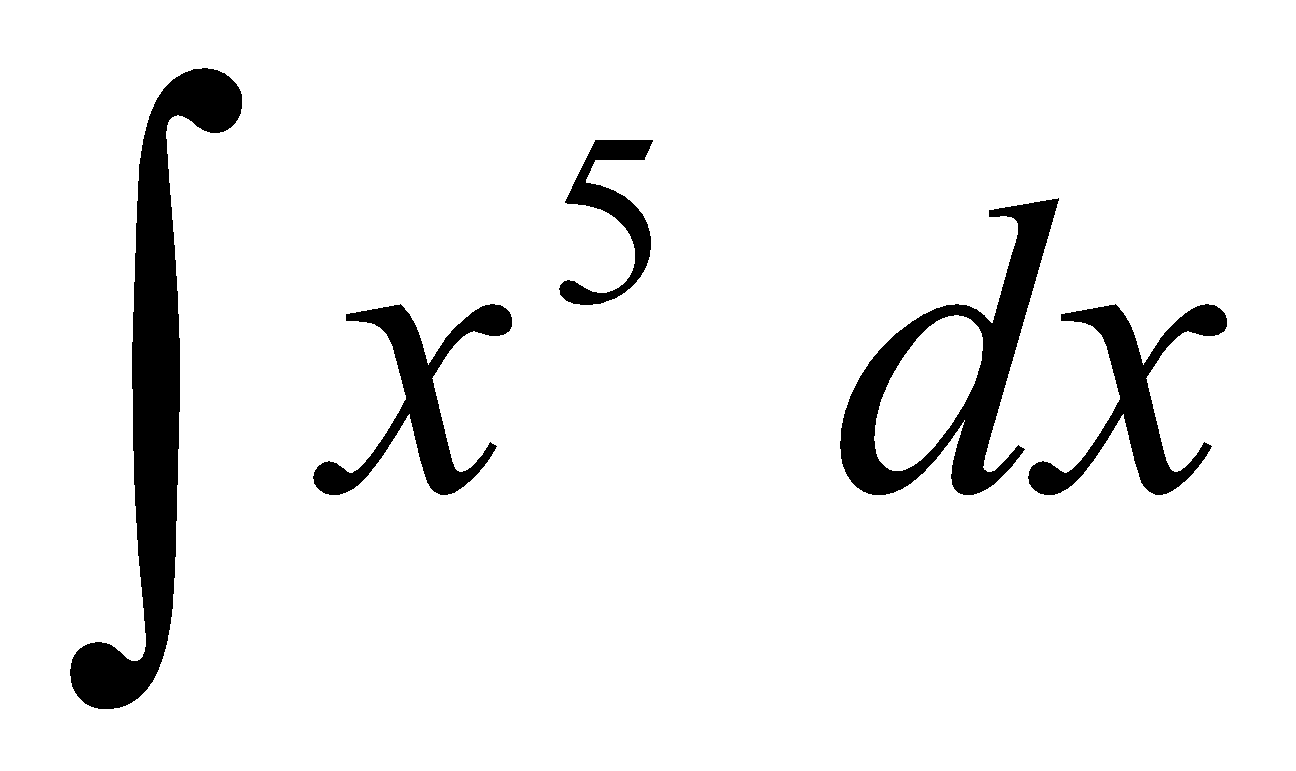



c)



d)




e)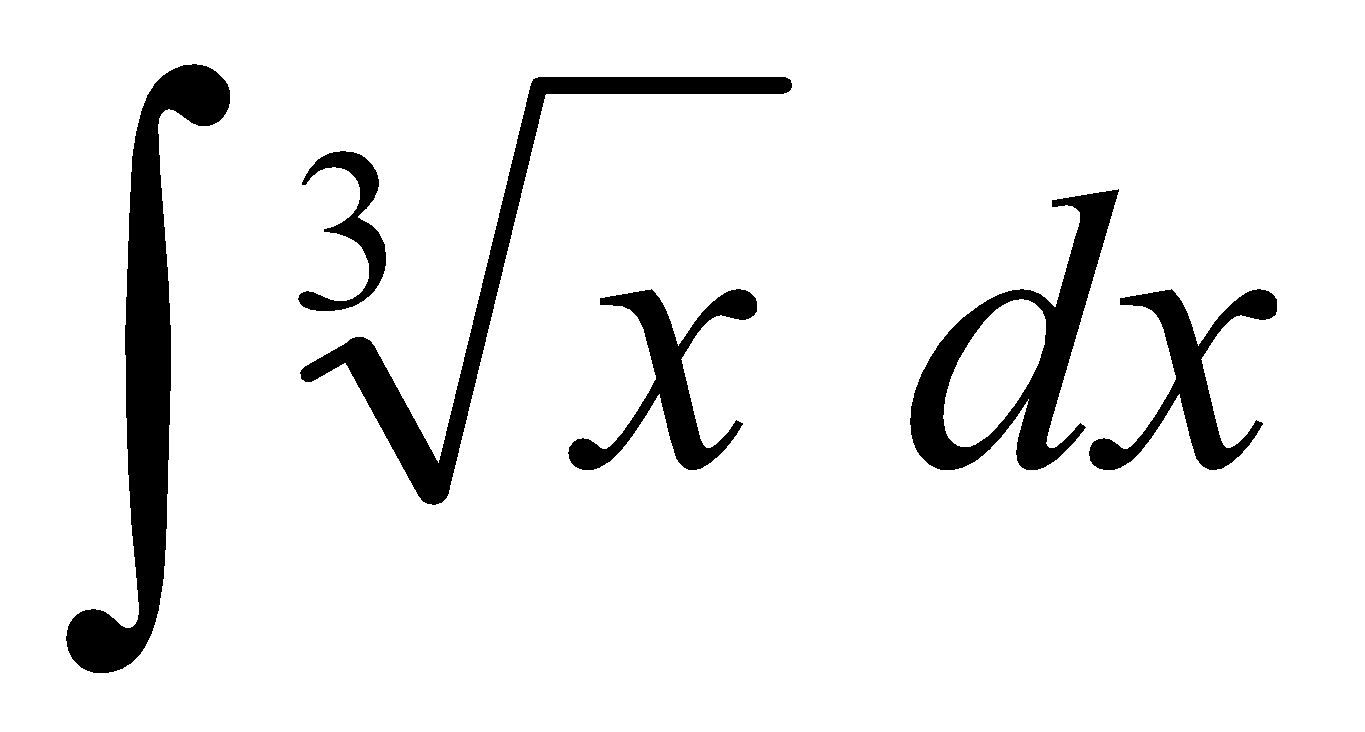  



f)




g)




h)




i)



j)

Integral definida: aplicación en el cálculo de áreas de recintos sencillos
La integral definida de f(x) en el intervalo 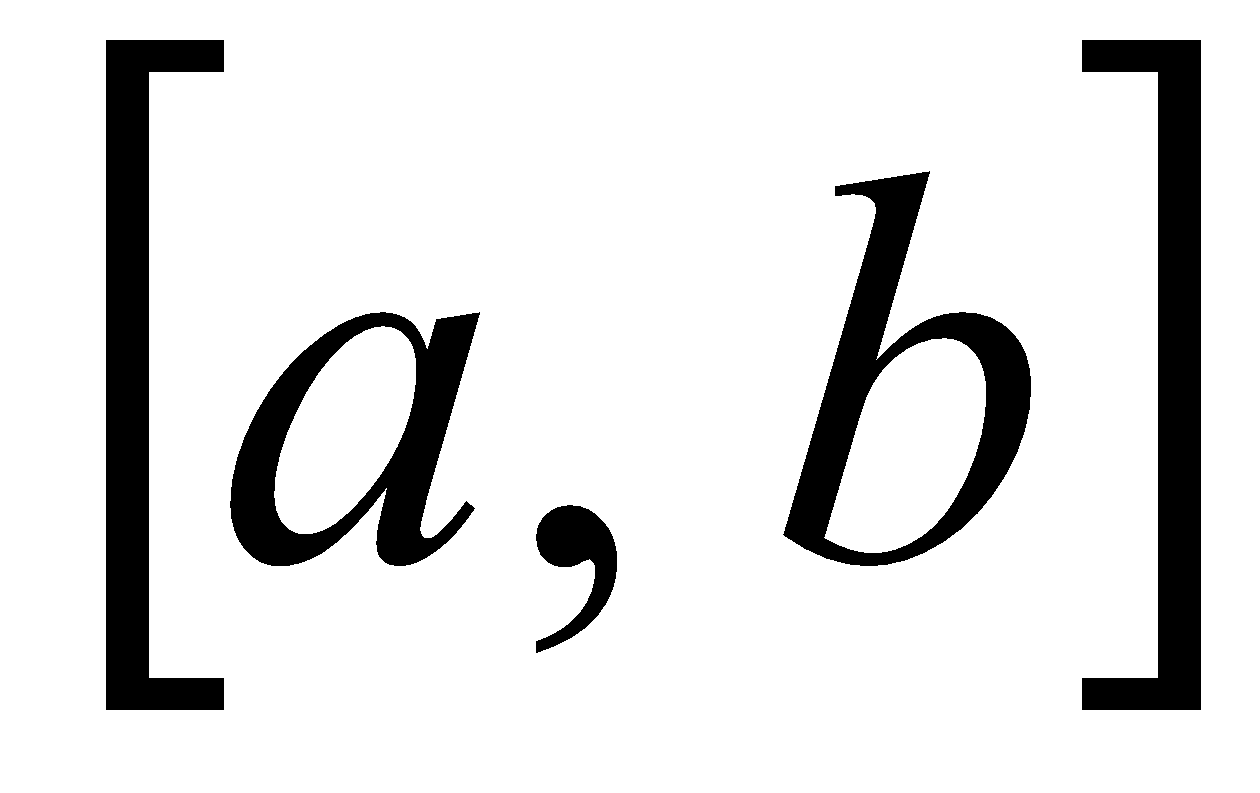, se representa mediante 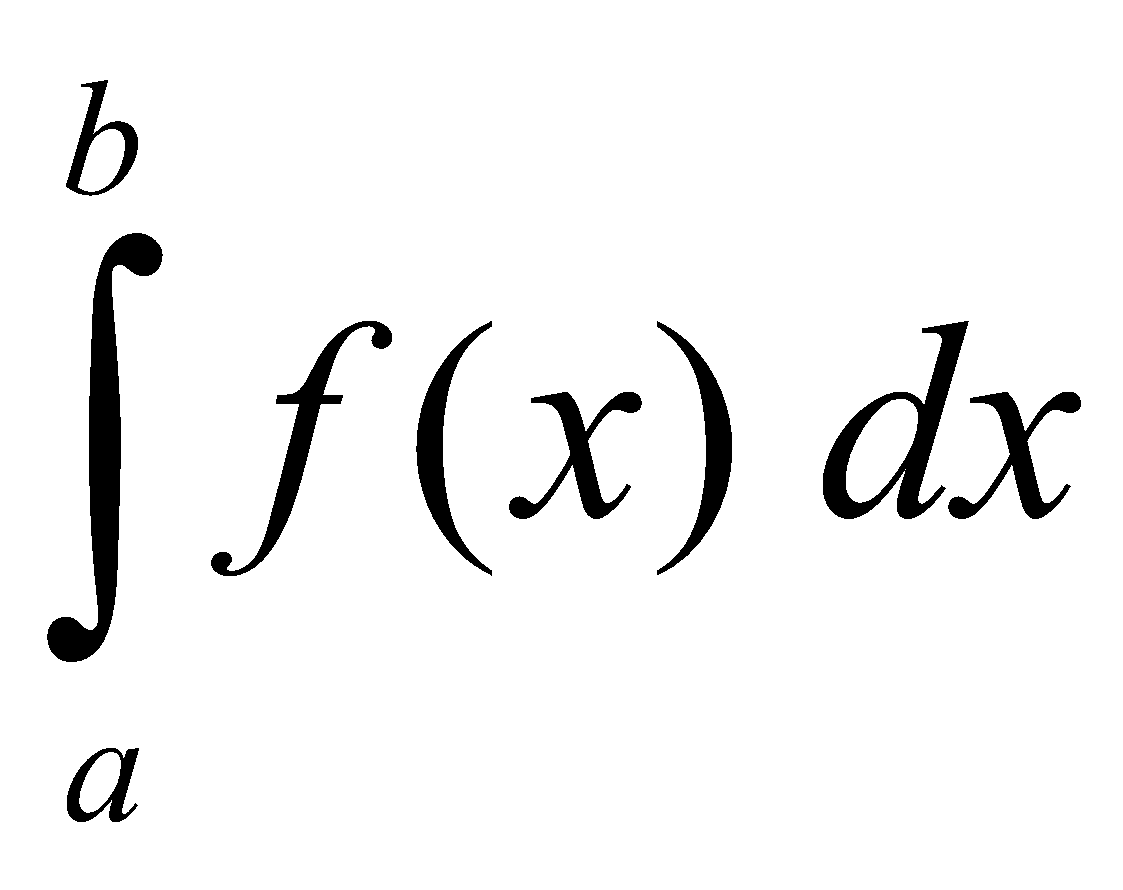, se lee como: integral definida de f(x) desde x=a hasta x=b, que son los límites de integración, y representa el área entre la función primitiva y los límites de  integración.
CÁLCULO DE ÁREAS DE RECINTOS SENCILLOS

Regla de Barrow: “La integral definida de una función en un intervalo es igual a la diferencia entre los valores que toma una función primitiva cualquiera en el extremo superior y en el inferior”. Es decir, si F(x) es una función primitiva de f(x), entonces: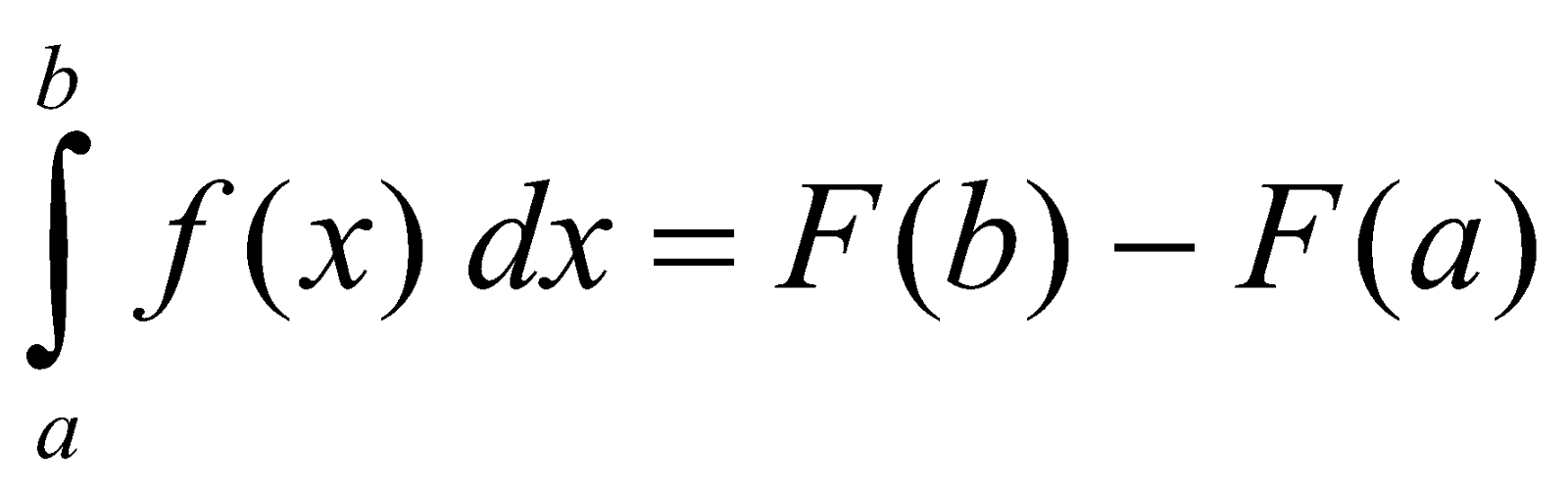

Recuerda: el área es siempre positiva (Calcular siempre el valor absoluto del recinto del área)
Ejemplo:
Calcula la integral definida siguiente: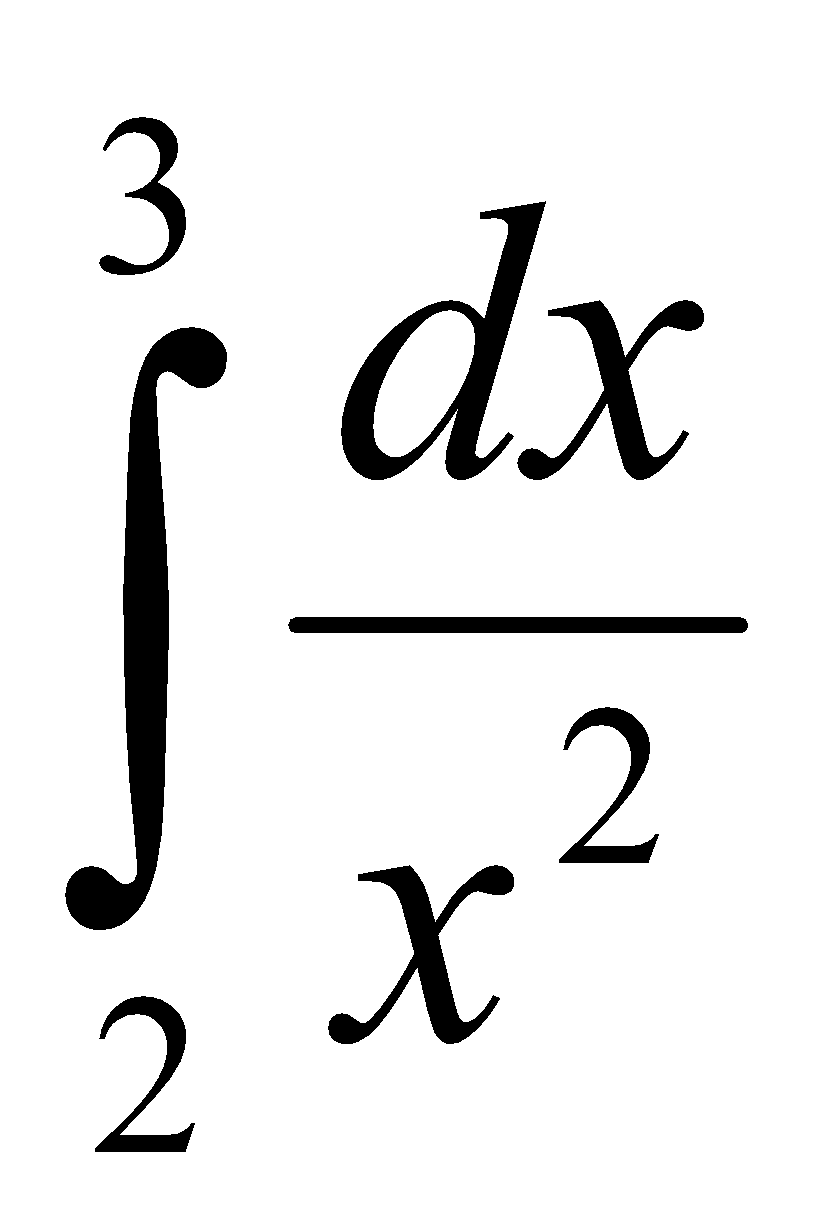








Sol: I= F(3)-F(2) = 1/6
a) Calcular el área encerrada por la curva y = x2, el eje de abscisas y las rectas
x = 1 y x = 2. (Representar la función y el área pedida)
 
 










Sol: Área = 7/3   unidades2
b) Determina el valor de








Sol: Área = 8 u2
c) Calcula el área de la región limitada por la función f(x)= -x2 +2x entre x=-1 y x= 4
  • Representar la función y área o hallar los límites de integración (a y b) que serán los puntos de corte (con el eje X, OX, u otra función). Para ello, hacer f(x)=0 y obtener las raíces, que serán los límites de integración.
  • Dividir el área en distintos recintos, si los hubiera.
  • Hallar la integral definida.
  • Calcular valor absoluto de los distintos recintos del área, si los hubiera.
  • Sumar las áreas (valores absolutos) de los distintos recintos, si los hubiera.












Sol: 28/3 = 9.333 u2
d) Calcula el área comprendida entre la curva y = 3x2-x+1, el eje X y las rectas x=0 y x=4.








Sol: Área = 60 u2
e) Halla el área bajo la “curva” y=3x-2 entre x=-1 y x=1










Sol: Área= 13/3   u2
f) Halla el área comprendida entre f(x)= x2-5   y   g(x)=-x2+5
  • Buscar soluciones de x2-5 =-x2+5 (serán los límites de integración)
  • Obtener la función diferencia f(x) –g(x)
  • Hallar la primitiva de la función diferencia
  • Calcular el área pedida (valores absolutos de cada recinto si los hubiera)












Sol: Área=
g) Calcula el área limitada por la curva y=x3-6x2+8x y el eje X











Sol: Área = 8 u2
h) Calcula el área del recinto limitado por la parábola de ecuación y = 9-x2 y el eje de abscisas









Sol: Área = 36 u2
i) Halla el área comprendida entre las parábolas y= 8-x2  e  y = x2












Sol: Área = 64/3  u2
j) Calcula el área del recinto limitado por la parábola y = 3x-x2 y la recta y= x-3













Sol: Área = 32/3  u2
k) Calcula el área del recinto limitado por la curva de ecuación y= 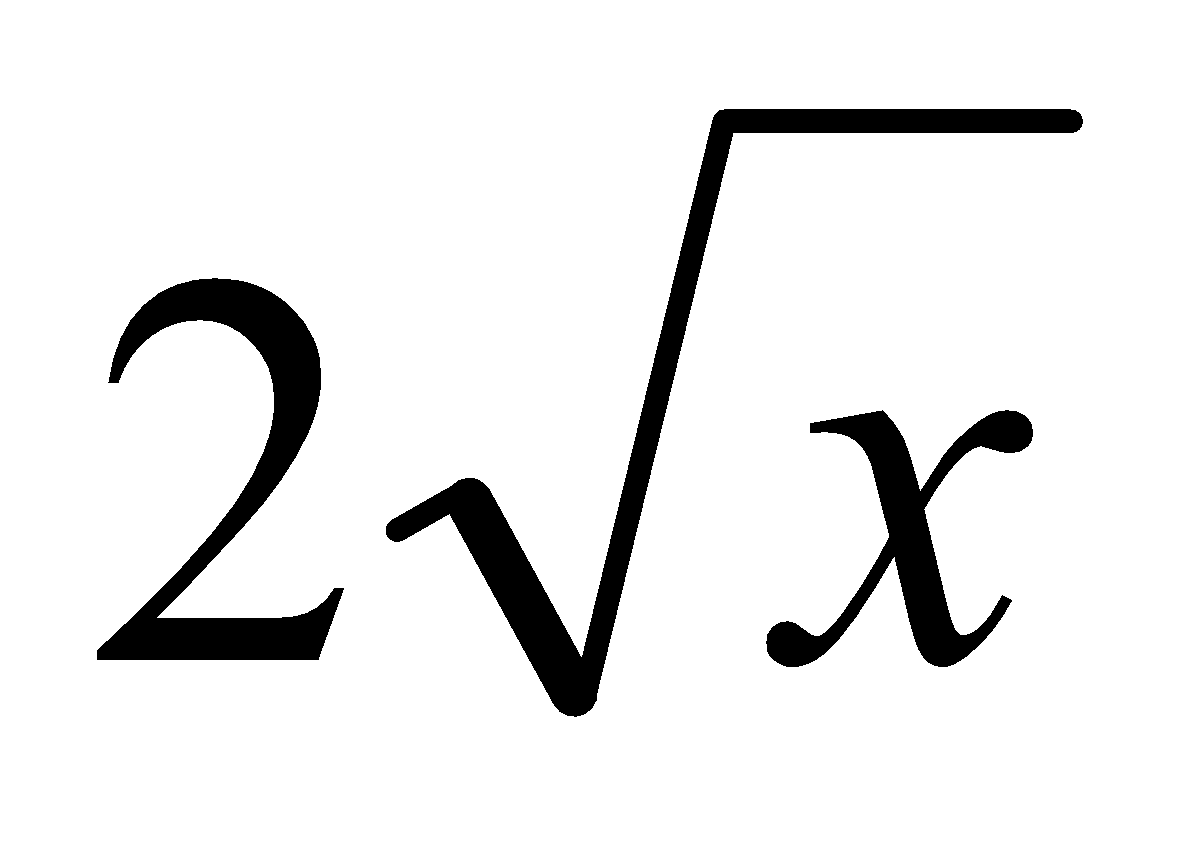y la recta y=x


















Sol: Área = 8/3 u2 =2.66 u2
l) Hallar el área del recinto limitado por eje OX, la curva x2 + 2 y las rectas x=0, x = 3.



















Sol: Área = 15 u2
ll) Hallar el área de la región del plano encerrada por la parábola y = x2 -3x +2   y el eje de abscisas.  (xv = -b/2a)













Sol: A = 1/6   u2
m) Calcula el área de la región del plano encerrada por las rectas x=1, x=4, el eje de abscisas y la función f(x)= x2 – 5x + 6














Sol: Área = 11/6   u2
n) Calcula el área delimitada por la función f (x) = cos x entre x = 0   , x = π/2







Sol: Área = 1 u2
ñ) Dadas las funciones f(x)=  -x2 + 2x,    g(x)= x/2 . Calcula el área de la región del plano encerrada por dichas gráficas.
















Sol: Área = 9/16   u2
o) Calcula el área limitada por la curva y = x2 - 5x + 6 y la recta y = 2x




















Sol: Área = 125/6   u2
p) Calcula el área limitada por las funciones  3y = x2 ,  y = -x2 +4x


















Sol: 6 u2
q) Calcula el área limitada por las funciones f(x)= x2– 1    y   g(x) = 4x- 4


















Sol: Área = 4/3   u2
Suscribirse a: Entradas (Atom)