DERIVADAS. APLICACIONES

DERIVADAS

Derivada de una función en un punto de abcisa x = a, es la tasa de variación instantánea de dicha función que se representa por f´(a) y se define como:

La derivada mide la variación de y, cuando hay una pequeña variación de x.

Haciendo . Si , entonces, 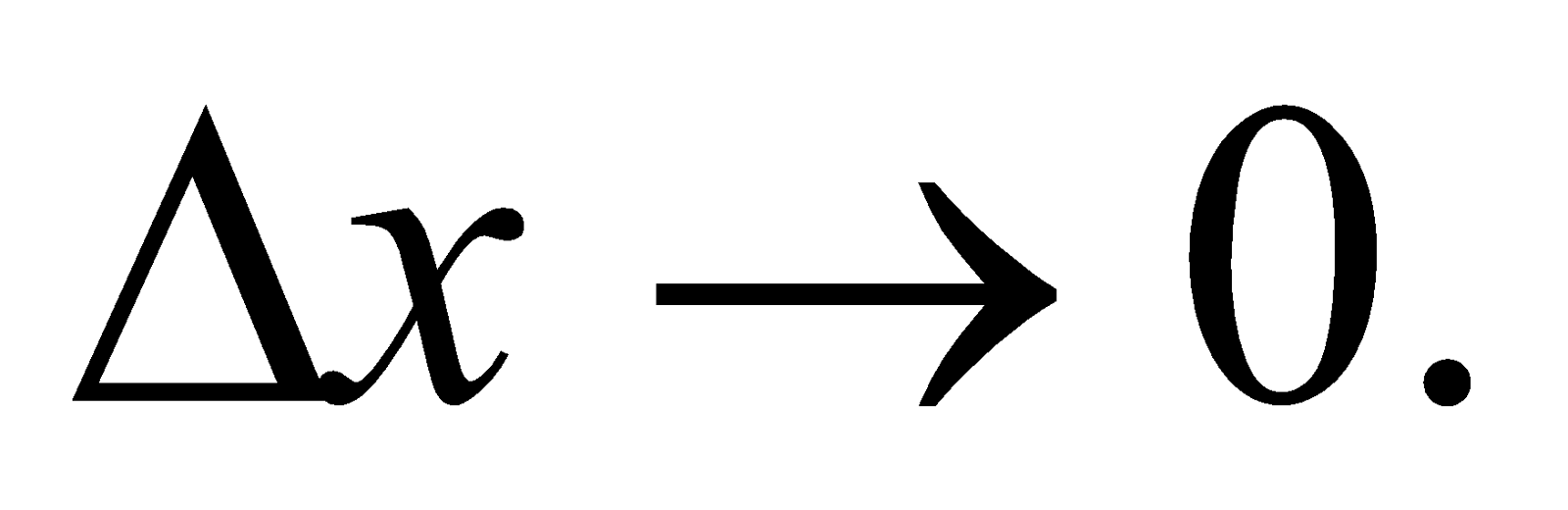Con lo que:

Por lo tanto, para que exista la derivada de una función en un punto, tiene que existir ese límite. Cuando no existe este límite, se dice que la función no es derivable en ese punto.

La derivada de una función en un punto coincide con la pendiente de la recta tangente a la gráfica de la función en ese punto.

EJERCICIOS (aplicando las reglas de derivación)

Denominaciones: Si expresamos la función de x como y , f(x) , o f(u)   entonces su derivada se expresa como y´, f´(x) o  f´(u).

Calcula la  derivada de las siguientes funciones:

1.  y = 7

2.  y =

3.  y = 5x3

4.  y =

5.  y = 3x2-5x+3

6.  

7.  

8.  y = (5x3-4x2)4

9.  y = 3·(4x2-5x)3

10.  

11.  y = (3x5-1) (4x2-6x)3

12. 

13.  

14.  

15. 

16.  y = sen x5

17.  y = sen (3x2-1)

18.  y = sen (5x4)

19.  y = sen3x4

20.  y = cos x3

21.  y = cos (5x3-x)

22.  y = cos (3x6)

23.  y = cos2 x3

24.  y = tg (3x2-5)3

25.  f(x) = 4x3 – 3x2 +2

26.  f(x) = tg x

27.  f(x) =

28.  f(x) = x ln x

29.  f(x) =

30.  f(x) =

31.  f(x) =

32.  f(x) =

APLICACIONES DE LA DERIVADA. RECTA TANGENTE

RECUERDA:

La derivada de una función en un punto coincide con la pendiente de la recta tangente a la gráfica de la función en ese punto.

Ecuación de la tangente en un punto (x = a) de una función:

Y – y0 = m (X – x0)    donde,   m = pendiente = y´(a)

33. Halla la ecuación de la recta tangente a la curva  y = x2 + 2x -1 en el punto de abscisa  x = 1.

Sol: Y = 4x - 2

34. Escribe la ecuación de la recta tangente a la curva  y = x3 -2x  en el punto de abscisa  x = 2.

Sol: Y = 10 x -16

35. Halla la pendiente de la recta tangente a la curva en el punto de abscisa x = 2. Escribe la ecuación de dicha recta.

Sol: m = 5;  Y = 5x - 3

36. Halla la ecuación de la recta tangente a la curva , en el punto de abscisa x = 4

Sol: Y = 5 x -15

37. Halla la ecuación de la recta tangente a la curva en el punto de abscisa   x = 0.

Sol: Y = 6 x

38. Escribe la ecuación general de la recta tangente a la curva f(x) = en el punto de abscisas x = 1

Sol: 5x - 9y – 11 = 0

39. Escribe la ecuación de la recta tangente a la curva  y = x3 -1  en el punto de abscisa  x = 1.

Sol: Y = 3x -3

40. Escribe la ecuación de la recta tangente a la curva en el punto de abscisas x=4.

Sol: y = x -7

APLICACIONES DE LA DERIVADA. 2. MÁXIMOS, MÍNIMOS, OPTIMIZACIÓN

Recuerda:

ESTUDIO DE LA MONOTONÍA (CRECIMIENTO VS DECRECIMIENTO) DE UNA FUNCIÓN:

• Si la derivada de una función en un punto es positiva, entonces la función es creciente en ese punto:

Si f´(a) > 0 entonces f(x) es creciente en el punto x=a

• Si la derivada de una función en un punto es negativa, entonces la función es decreciente en ese punto:

Si f´(a) < 0 entonces f(x) es decreciente en el punto x=a

MÁXIMOS Y MÍNIMOS DE UNA FUNCIÓN:

• La derivada de una función en sus extremos relativos (posibles máximos y mínimos relativos) es cero. (En estos puntos la pendiente de la tangente de la función es cero, horizontal, ni creciente ni decreciente).

• Para confirmar la existencia de máximos o mínimos hay que estudiar la derivada segunda de la función en dichos puntos.

• Una función f(x) tiene un MÁXIMO en el punto x=a, si en dicho punto la derivada primera se anula y la derivada segunda es negativa:

Si f´(a) = 0 y f´´(a) < 0 , entonces f (a) : máximo   

• Una función f(x) tiene un MÍNIMO en el punto x=a, si en dicho punto la derivada primera se anula y la derivada segunda es positiva:

Si f´(a) = 0 y f´´(a) > 0 , entonces f (a) : mínimo   

41. Estudia los intervalos de crecimiento y decrecimiento de la función: . Dibuja la función.  

• Hallar f´(x)
• Igualar f´(x) = 0 .  Resolver la ecuación, es decir:

Hallar x que hace cero a f´(x) (para ello: f´(x) = 0 y hallar el valor de x.  Supongamos que ese punto crítico o singular es “a” ). Seguir, según convenga uno de los siguientes pasos:

• Calcular f´(a) a la izda y drcha de “a”. y/o (¿crec o decr?)
• Hallar f´´(a) (¿máx o mín?)
• O, dibujar la curva y encontrar los máximos o mínimos

Sol: x = -1 mínimo. Decr  en (-∞, -1) y crec   en (-1, + ∞)

f´´(x)=2 para todo x, entonces  x=1 es un mínimo

42. Halla los puntos críticos (singulares) de la función: y define qué tipo de punto es (máx, mín,..)

Sol: x = -1, mínimo; x =-2, máximo; x = -3 mínimo

43. Halla los máximos y mínimos de la siguiente función:

g (x) =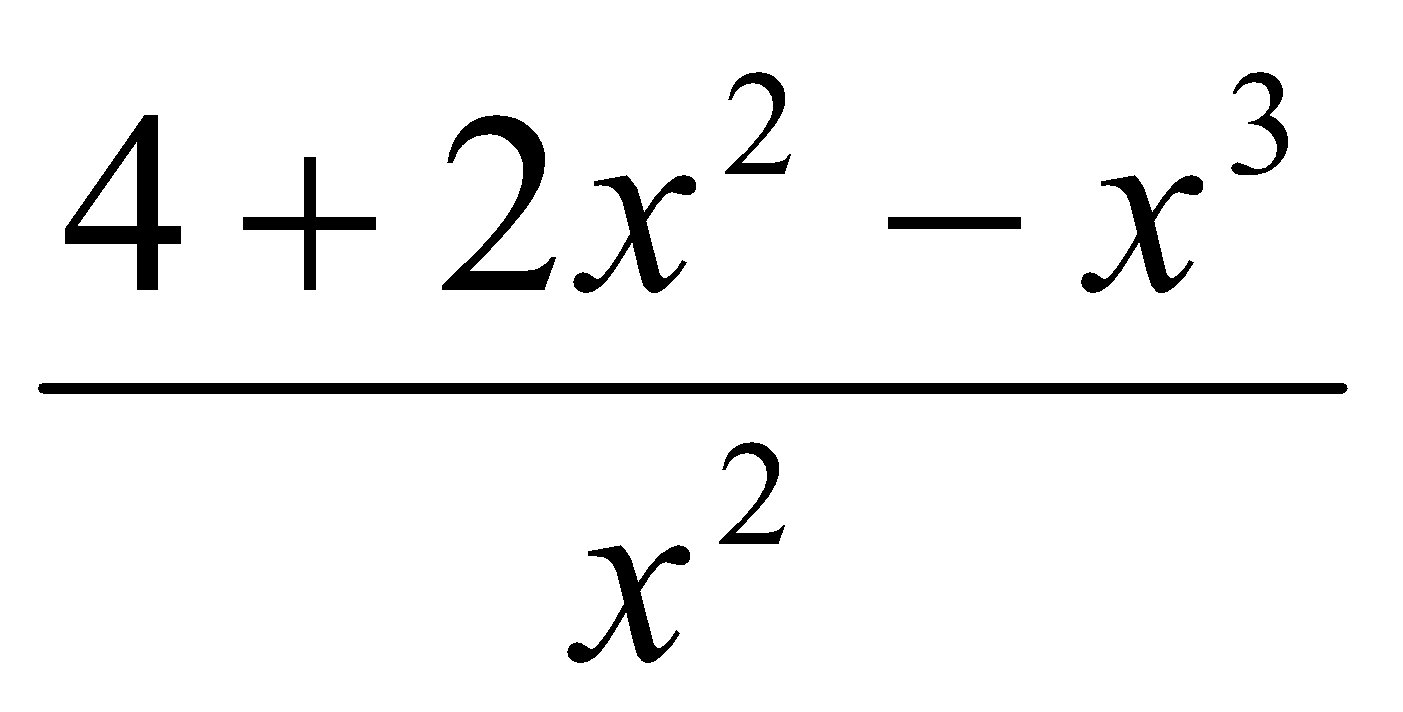

Sol:  (-2, 5) es un mínimo

44. Halla los máximos y mínimos de la función

Sol: máx (1, 2);    mín (-1, -2)

45. Halla los valores de a y b en y = x2 + a x +b que pasa por el punto P (-2, 1) y tiene un extremo relativo (máximo o mínimo) en el punto x = 3.

Sol: a = -6;   b = -15

46. Halla los valores de a y b en y = x2 + a x +b que pasa por el punto P (-2, 1) y tiene un extremo relativo (máximo o mínimo) en el punto x = -3.

Sol: a = 6;   b = 9

47. Halla dos números cuya suma sea 20 y cuyo producto sea el mayor posible.

Sol: x = 10;  y = 10

48. Calcular las dimensiones del mayor rectángulo cuyo perímetro sea 40.

Sol: x = 10;   y = 10

49. Un pastor quiere vallar un campo rectangular de 3600 m2 de superficie para hacer un corral. ¿Cómo le indicaríamos las dimensiones  para que el coste fuera mínimo?

Sol: x = 60 m;   y = 60 m

50. Descomponer 18 como suma de dos números positivos, de manera que el producto de uno de ellos por el cuadrado del otro sea máximo.

Sol: x = 6;   y = 12

51. Un pastor dispone de 1000 metros de tela metálica para construir un cerco rectangular aprovechando una pared ya existente. Halla las dimensiones del cerco a fin de el área encerrada sea máxima.

Sol: x = 500 m; y = 250 m

52. Un depósito abierto de latón con base cuadrada y capacidad para 4.000 litros, ¿qué dimensiones debe tener para que su fabricación sea lo más económica posible?

Sol:  20 dm de lado de la base y 10 dm de altura

53. La función de coste total de producción de x unidades de un determinado producto es: . Se define la función de coste medio por unidad como . ¿Cuál debe ser la producción para que sea mínimo el coste medio por unidad?

54. Se sabe que el rendimiento, r en %, de un estudiante que realiza un examen de una hora viene dado por siendo , en horas. ¿Cuándo es el rendimiento máximo?

55. Se ha estudiado el rendimiento de los empleados de una oficina a medida que transcurre la jornada laboral. (Dicho rendimiento corresponde al número de instancias revisadas en una hora). La función que expresa dicho rendimiento es: siendo el número de horas transcurridas desde el inicio de la jornada laboral.

Determina cuándo se produce el máximo rendimiento y cuándo se produce el mínimo rendimiento.

Halla la tasa de variación media (t.v.m.) del rendimiento 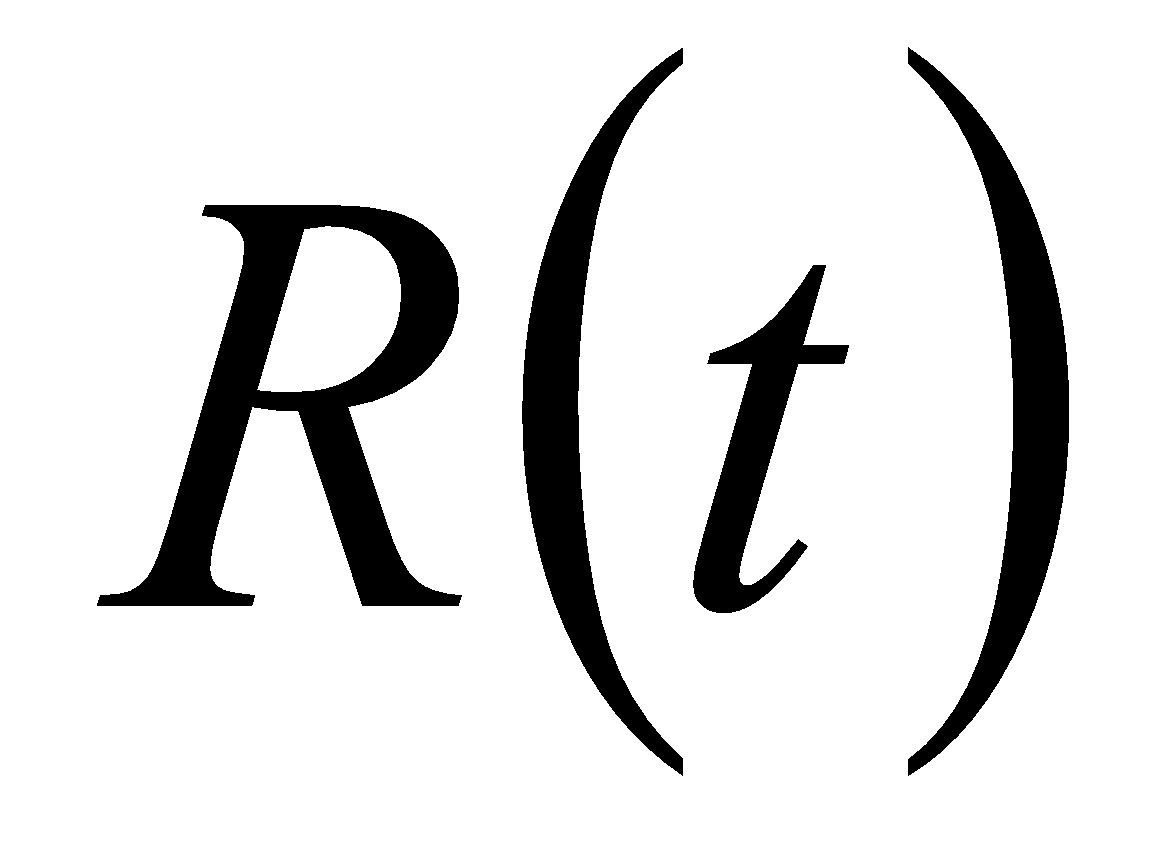entre y

         (nota: 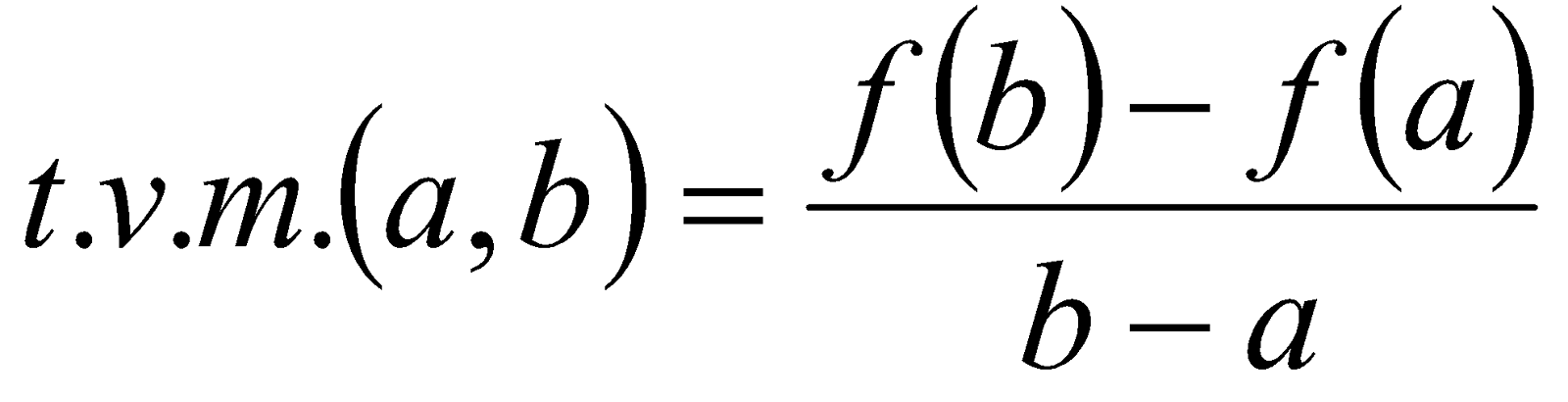). Dibuja la función para t = 0, t = 1; t = 2; t = 3;

        t = 4; t = 5 y t = 6.