EL NÚMERO ENTERO. CONJUNTO Z. OPERACIONES
Podemos definir un número entero como aquel que resulta de restar dos números naturales cualesquiera. (7 - 7 = 0 entonces, 0 es un número entero).
Llamamos Z al conjunto de los números enteros, Z+ al conjunto de los enteros positivos y Z- al conjunto de los enteros negativos. Así, Z es igual a Z+, Z-, 0.
- Valor absoluto de un número entero
El valor absoluto de un número entero es el valor del número prescindiendo del signo; puede decirse, tambien, que el valor absoluto de un número entero es el valor positivo de dicho número.
Se simboliza el valor absoluto colocando el número entre dos barras:
Ejemplo: 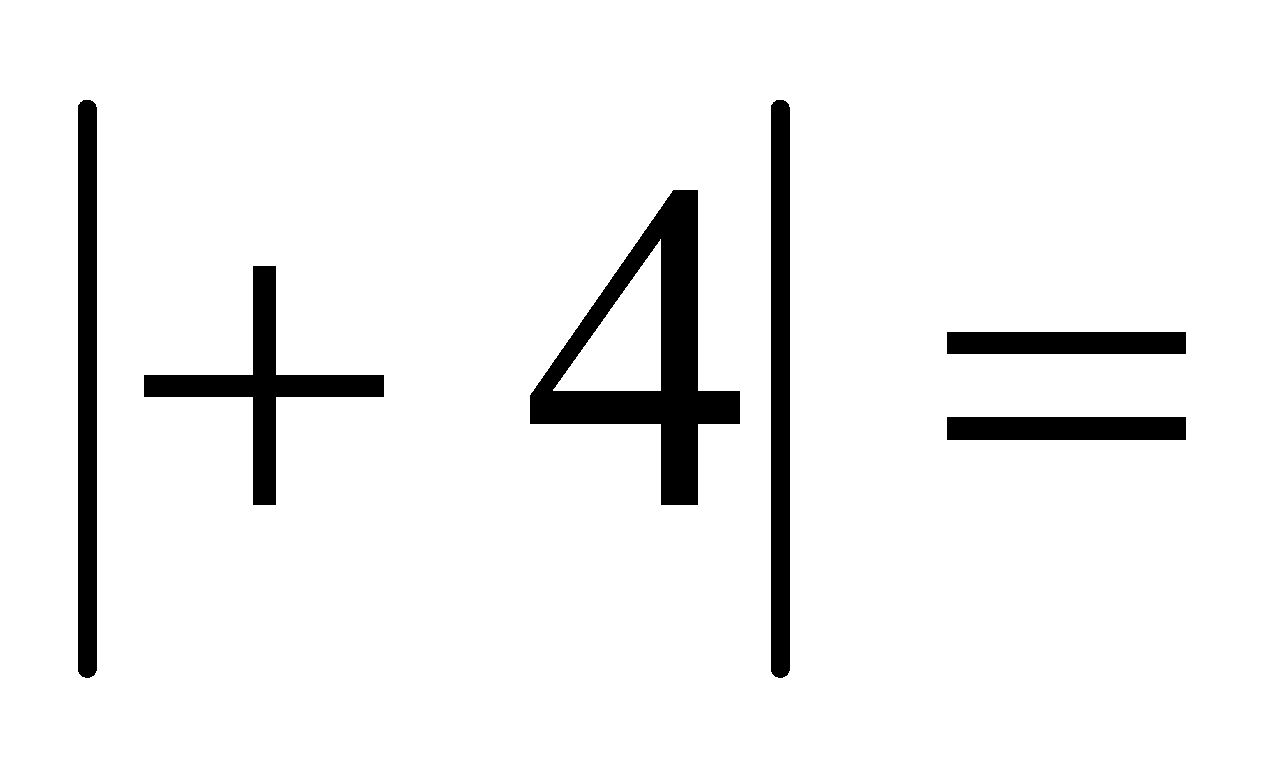 ;
; 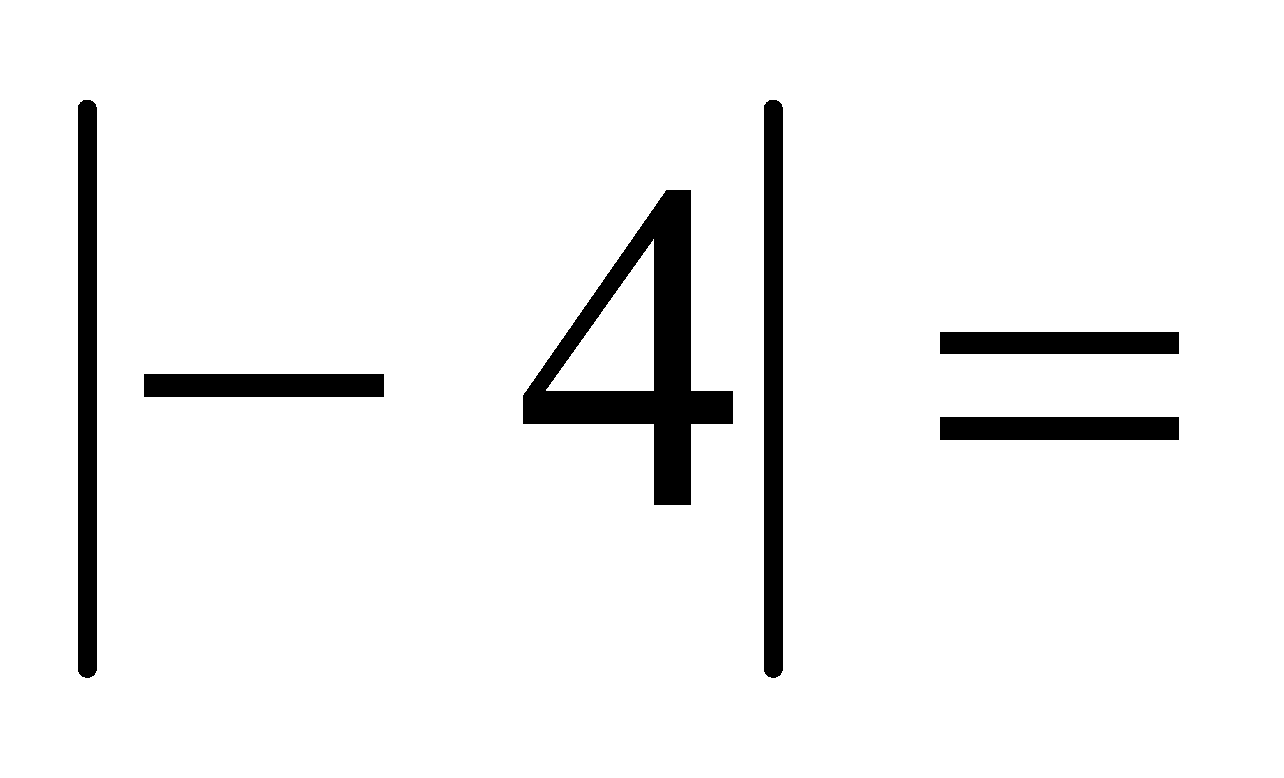


- Reglas de la SUMA de los números enteros:
Para sumar dos números enteros de signos iguales se suman los valores absolutos y se pone el mismo signo. 4 + 13 =
-8 – 56 =
Para sumar dos números enteros de signos distintos se restan los valores absolutos y se pone el signo del número que tenga mayor valor absoluto. +6 -14 =
-6 + 14 =
Significado de los paréntesis: En el cálculo operativo, un paréntesis indica la prioridad de la operación encerrada en ese paréntesis. Una vez efectuada la operación se elimina el paréntesis. Tambien se usan corchetes y llaves para indicar operaciones entre paréntesis. (6 – 11) + 4 =
7 – (4 – 2) =
Un signo negativo anterior a un paréntesis modifica el signo del resultado de la operación de dicho paréntesis. – (13 + 4) – (7 – 9) =
Entre dos signos (+,-; · , +; · , -; …) siempre habrá que intercalar un paréntesis.
Ejemplos: 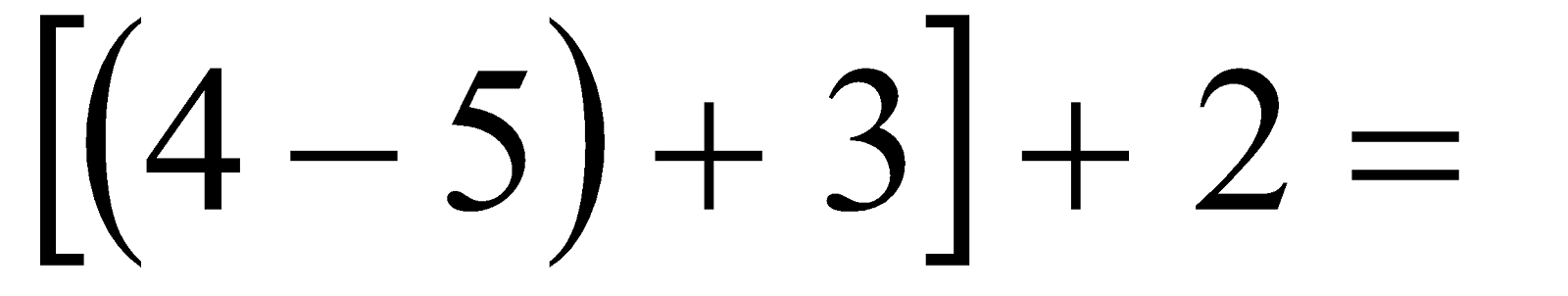
Ejercicios:
- 2 + 6 =
- 7 – (-3) =
- (-2) – 6 =
- (-2) – (-6) =
- 7 – (-3) =
- (-2)+(-6) =
- (-7) + (-3) =
- (-6) – (-3) =
- Propiedades de la SUMA de los números enteros:
Las propiedades de la suma de los números enteros son la mismas que las de la suma de los números naturales (asociativa, conmutativa, elemento neutro) y, además tiene:
Opuesto de un número entero: el opuesto de un número entero es aquel que sumado al entero da como resultado cero: -a + a =0
Ejemplo: el opuesto de +3 es:
El opuesto de -11 es:
Nota: Los números enteros positivos podemos representarlos con el signo (+) delante o sin él. Ejemplo: 4 = +4 +7895 =
- Reglas de la MULTIPLICACIÓN de los números enteros
Regla de los signos:
Signos iguales: 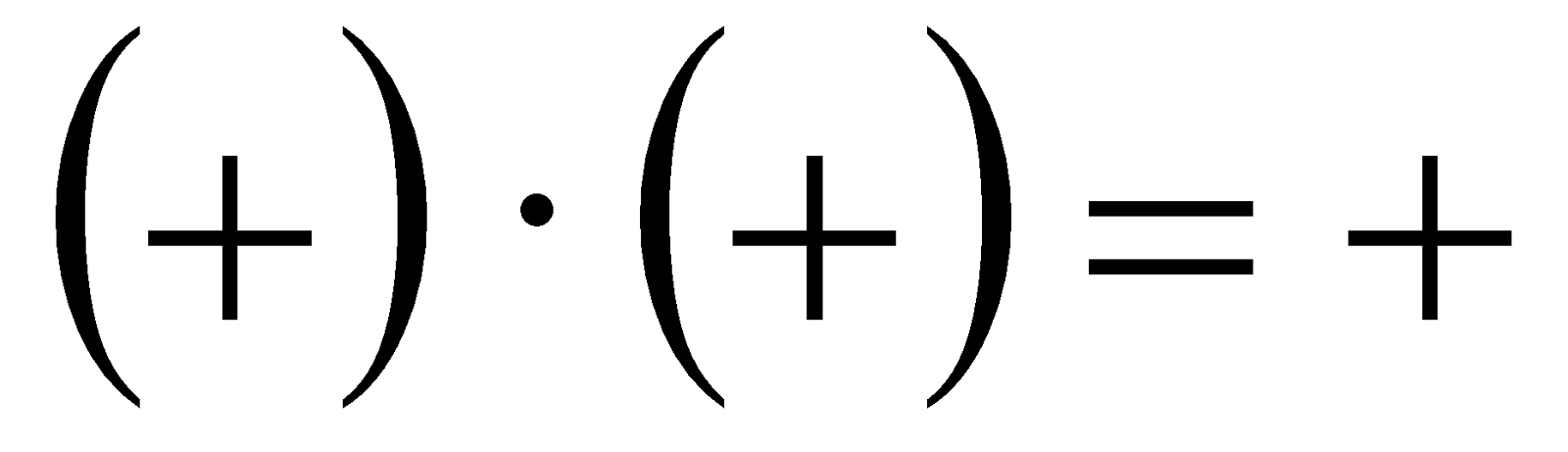

Signos distintos: 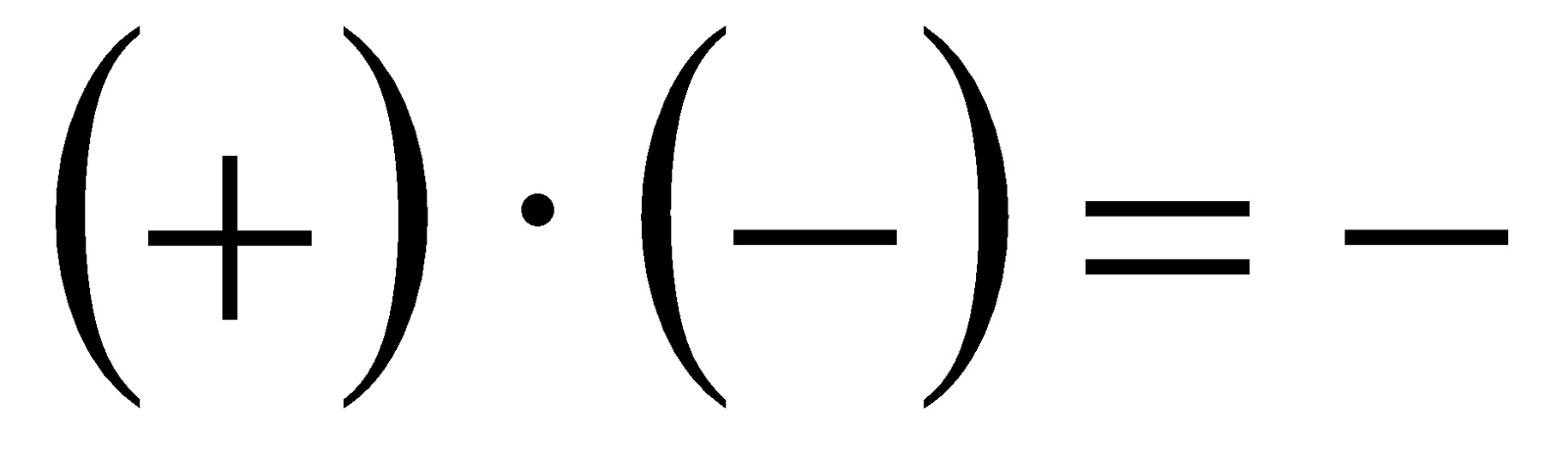

Es decir, si los signos de los dos factores son iguales el resultado es positivo; y si los signos de los factores son distintos, el resultado es negativo.
Ejercicios:
(+3) · (-4) =
(-3) · (+4) =
(-3) · (-4) =
(+3) · (+4) =
Un signo negativo anterior a un paréntesis modifica el signo del valor incluído en dicho paréntesis.
-(-3) = (-1) · (-3) = +3 = 3
-(+3) = (-1) · (+3) = -3
En cuanto a las propiedades del producto de los números enteros, son las mismas que las de los números naturales, es decir, asociativa, conmutativa, elemento neutro y distributiva respecto a la suma.
- ORDENACIÓN de los números enteros
Los números enteros se pueden ordenar de menor a mayor y viceversa.
-4 es menor que -3, menor que -2, …
-4 < -3 < -2 <…