ECUACIONES

ECUACIONES

Identidad: es una igualdad entre dos expresiones equivalentes.

Ej1:   (x+1)2 = x2 +2x +1   es una identidad, ambas expresiones algebraicas son equivalentes. Los valores numéricos de los dos miembros coinciden siempre, independientemente del valor que se asigne a x.

Ecuación es una igualdad entre dos expresiones algebraicas no equivalentes.

En una ecuación se indica que los valores numéricos coinciden, pero no siempre, sino sólo para alguno o algunos de los valores de las letras; esos valores son las raíces o soluciones de la ecuación.

Ej2:   2x + 1 = 3  es una ecuación (para algún valor de x, x=      en este caso, los valores numéricos de ambos miembros coinciden, es decir, x =     es la raíz de la ecuación)

Resolver una ecuación es determinar sus raíces o soluciones. Al sustituir la incógnita por su raíz o solución, la igualdad se cumple.

CLASES DE ECUACIONES

RESOLUCIÓN DE ECUACIONES FRACCIONARIAS

Se suprimen los denominadores obteniendo el denominador común (mcm, de todos ellos) y/o, aprovechando la propiedad de las fracciones polinómicas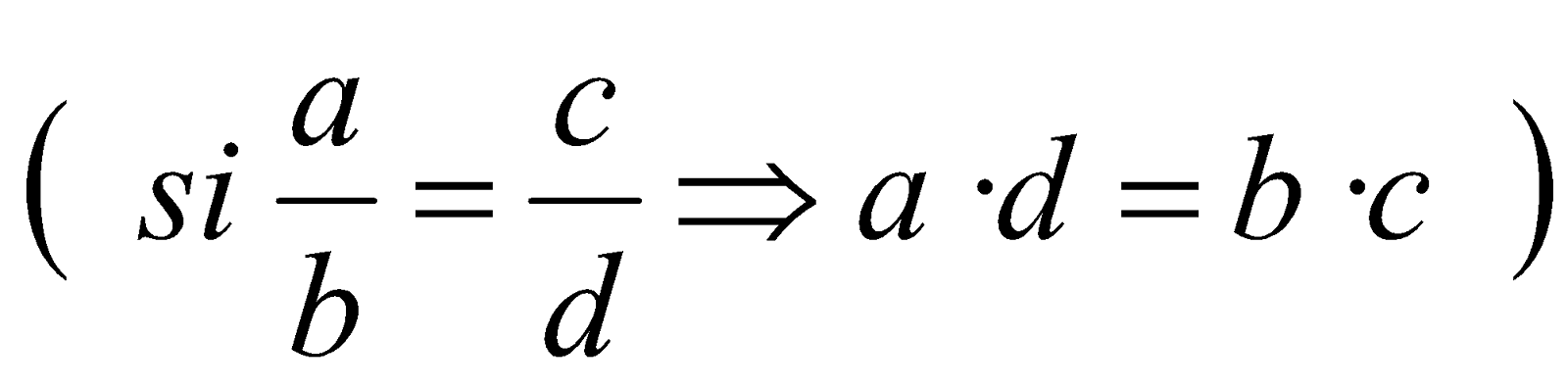

COMPRUEBA SIEMPRE LAS SOLUCIONES de todo tipo de ecuaciones, sustituyendo el valor de la incógnita en la ecuación original.

1. Resuelve: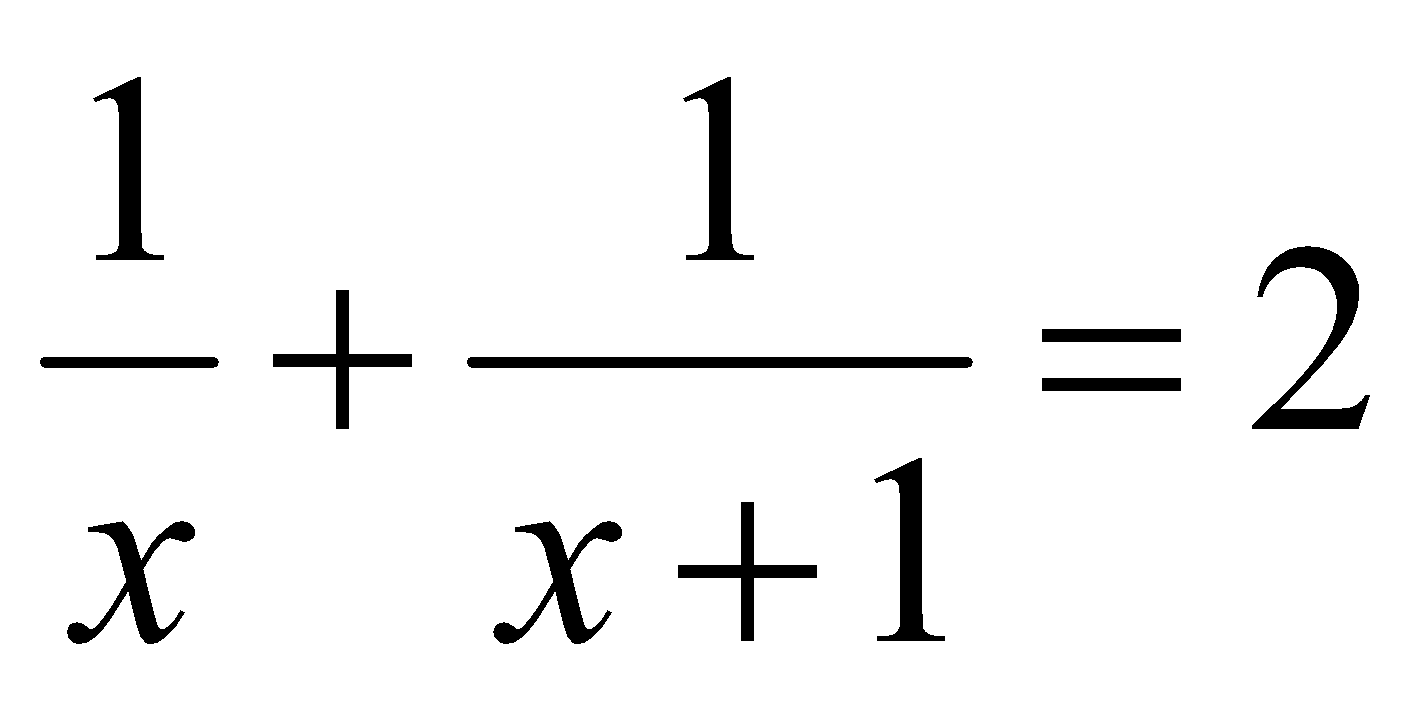

2. Resuelve:

3. Resuelve:

4. Resuelve: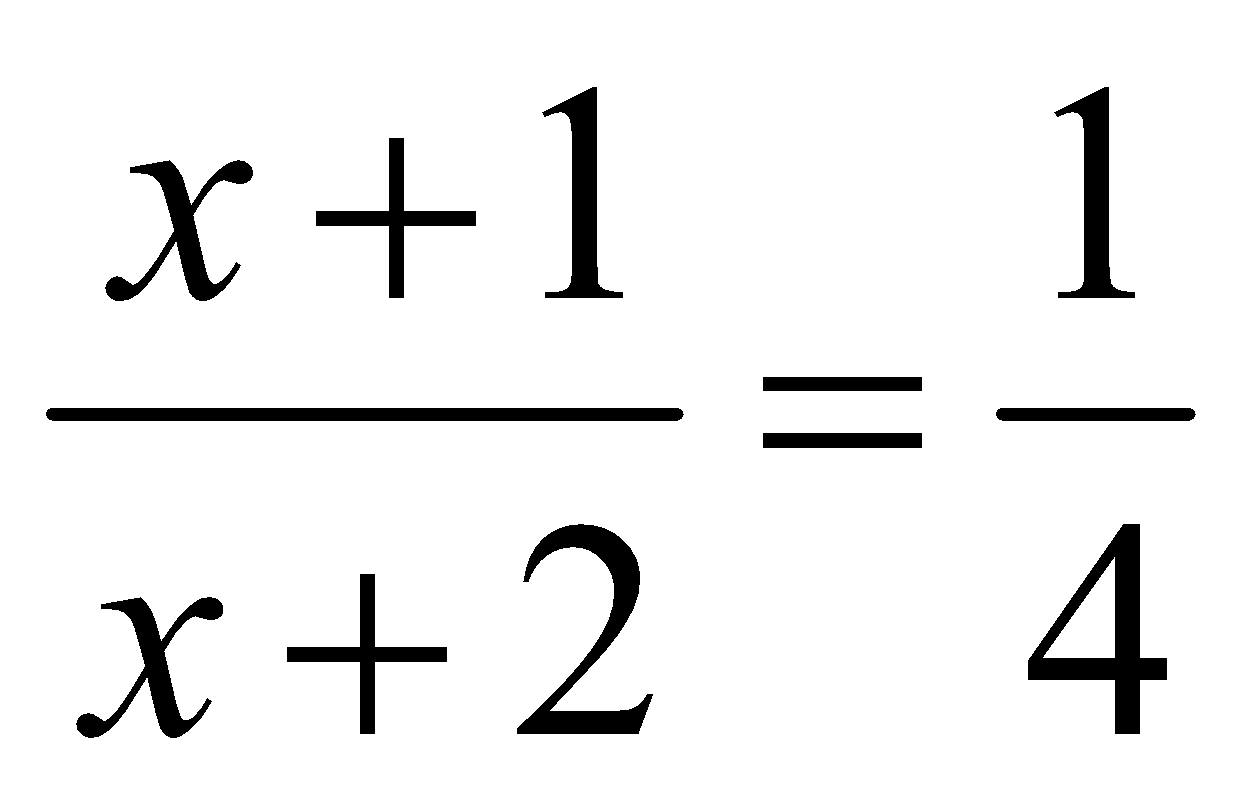

5. Resuelve: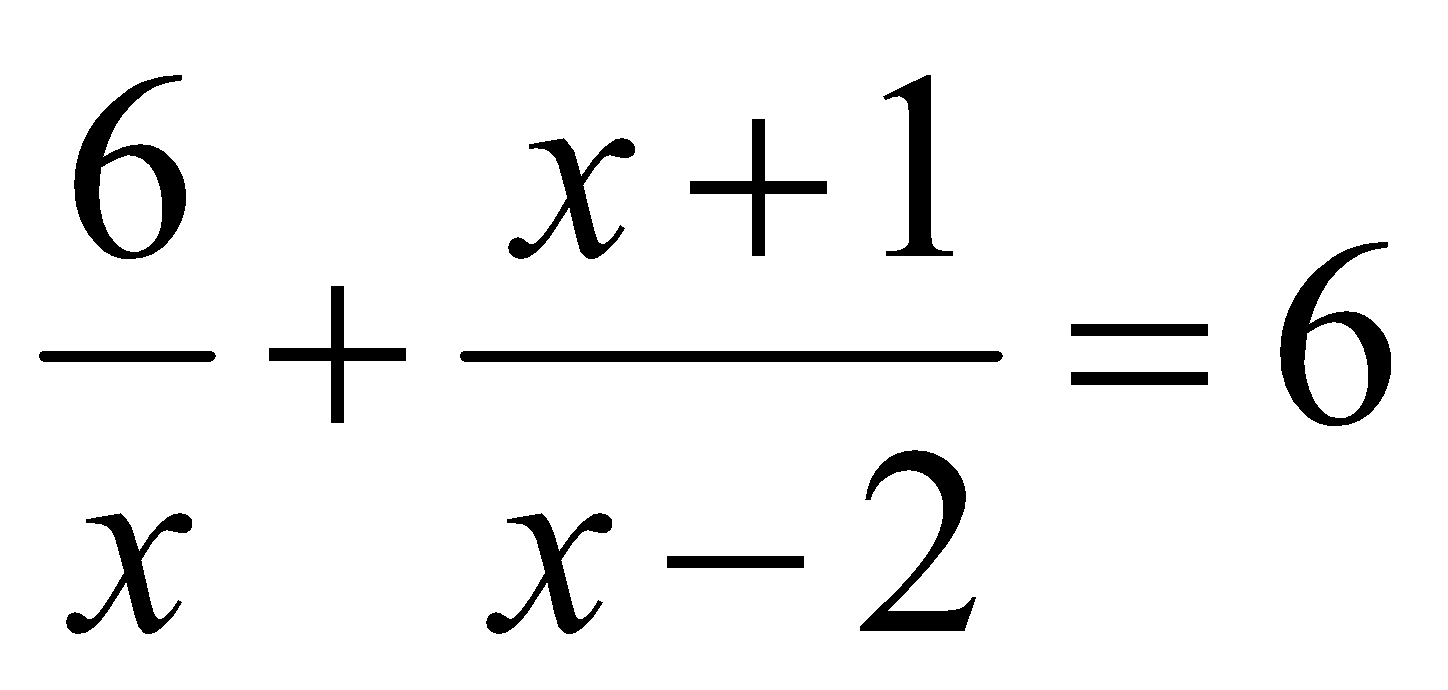                   

RESOLUCIÓN DE ECUACIONES IRRACIONALES

Para resolver ecuaciones en las que la incógnita está afectada por alguna raíz:

• Aísla la raiz cuadrada en un miembro.

• Eleva ambos miembros al cuadrado.

• Si hubiera más de un término con la incógnita en raíz: 1º aislar una de las raíces; 2º elevar ambos miembros al cuadrado; 3º repetir los pasos anteriores cuantas veces sea necesario.

En este proceso (elevar al cuadrado los miembros de la ecuación) pueden aparecer soluciones falsas que hay que rechazar. Es fundamental comprobar todas las soluciones.

6. Resolver las siguiente ecuaciones:

a)

b)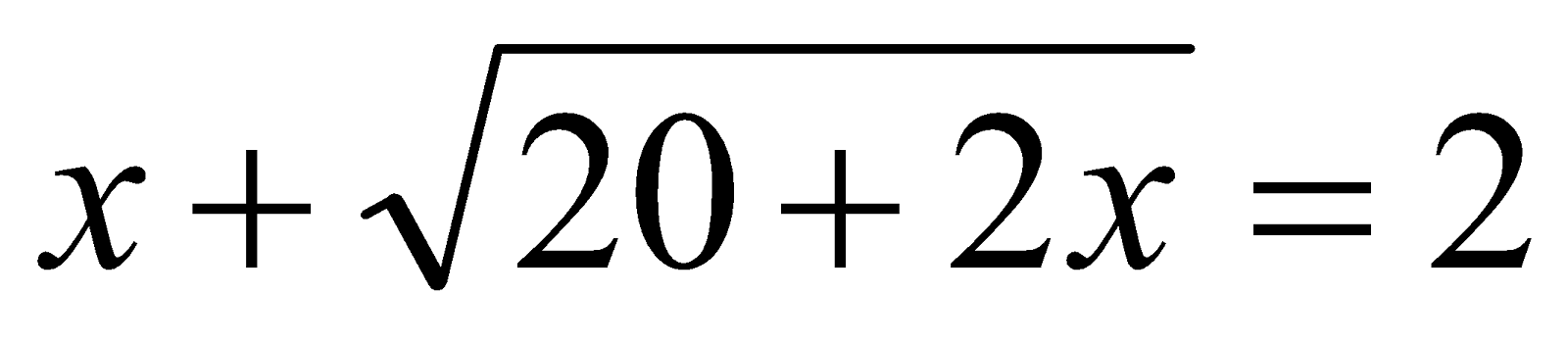                        

7. Resuelve:

8. Resuelve:

ECUACIONES POLINÓMICAS DE PRIMER GRADO (ecuaciones LINEALES)

Una ecuación polinómica de primer grado es aquella que, una vez reducida a su expresión más sencilla queda de la forma:  ax + b = 0

 

                     

Resolución de ecuación polinómica de primer grado:

• Se efectúan todas las operaciones algebraicas posibles en ambos miembros de la ecuación.

• Simplificar la ecuación cuanto sea posible, quedando reducida a la forma ax + b=0.

• Despejar la incógnita.

9. Resuelve: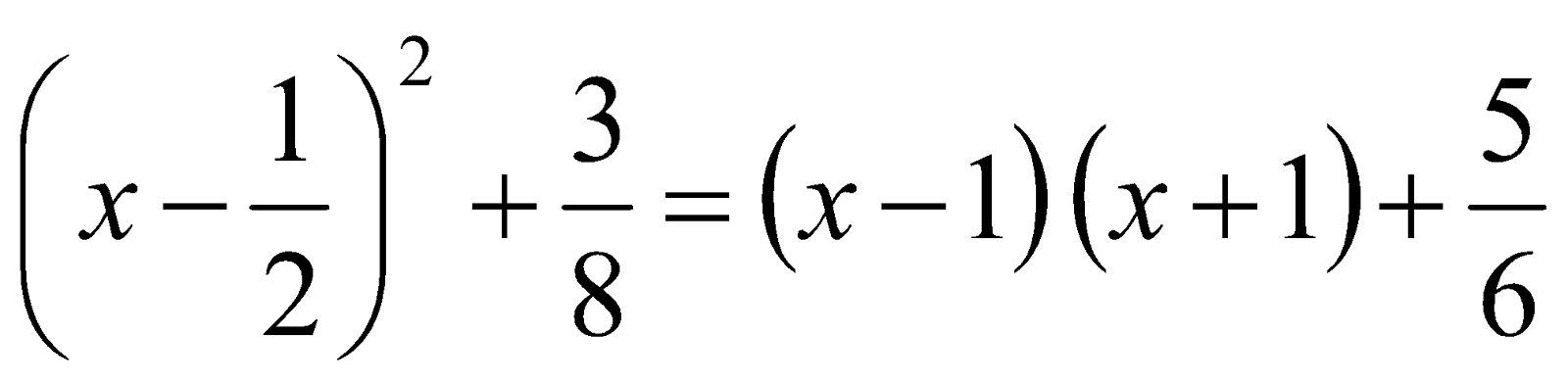

Sol: x = 19/24

10. Resuelve: (x +1)2 – (x-1)2 =8

11. Resuelve:

12. Clara tiene 31 años y su hijo 5. ¿Cuántos años tendrá Clara cuando su edad sea el doble que la de su hijo?

13. Determinar tres números enteros consecutivos, sabiendo que su suma es 636.

14. Determinar dos números naturales consecutivos, sabiendo que la diferencia de sus cuadrados es igual a 15.

ECUACIONES POLINÓMICAS DE SEGUNDO GRADO

Una ecuación polinómica de segundo grado es aquella, que una vez reducida a su expresión más sencilla, queda de la forma:   ax2 + bx + c = 0   donde .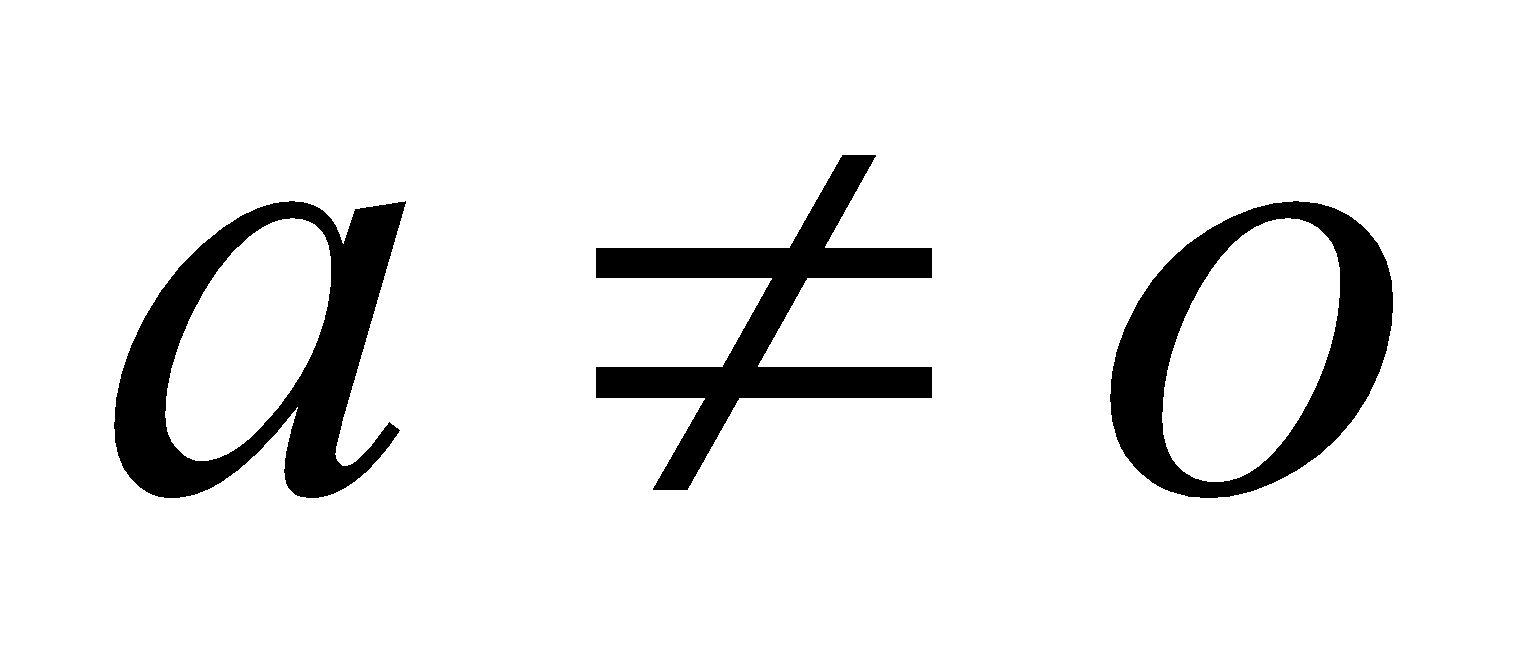

Cuando todos los coeficientes son distintos de cero la ecuación es completa; si alguno de los coeficientes es cero, la ecuación es incompleta. Veremos ahora las ecuaciones incompletas:

ax2 = 0

ax2 + bx = 0

ax2 + c = 0  

• Resolución de la ecuación incompleta ax2 = 0

Ej3 = Resuelve:  5x2 = 0

En consecuencia, todas las ecuaciones tipo   ax2 = 0  tienen como única solución    x = 0  (solución doble)

• Resolución de la ecuación incompleta ax2 + bx = 0   (Sacar x como factor común)

En consecuencia, todas las ecuaciones incompletas de este tipo poseen dos soluciones, una de las cuales es siempre 0.

Ej4: Resuelve: 2x2 + 6x = 0

• Resolución de la ecuación incompleta ax2 +c  (despejar x2; raíz cuadrada a ambos términos)   

Ej5 = Resolver: 2x2 -8 = 0

Resuelve cada una de las siguientes ecuaciones incompletas:
Ecuación	Resolución	Solución
7x2 = 0
3x2 – 75 = 0
x2 -7x = 0
4x2 + 9 = 0
4x2 + 6x = 0

Resolución de la ecuación completa:     ax2 + bx + c = 0

Aplicamos la fórmula del discriminante (b2 -4ac):

Resuelve cada una de las ecuaciones completas
Ecuación	Resolución	Solución
x2 – 7x + 12 = 0
x2 + 10x + 25 = 0
2x2 + 3x + 5 = 0
x2 – 7x + 10 = 0
x2 – x - 6 = 0
x2 – 2x – 1 = 0
9x2 – 6x + 1 = 0

RESOLUCIÓN DE ECUACIONES DE GRADO SUPERIOR A DOS

• Según el caso aplicamos Ruffini, sacamos x como factor común, etc…

Resuelve cada una de las ecuciones
Ecuación	Solución
x3 - 5x2 + 10x – 8 = 0	x = 2
x3 + 12x2 + 38x + 15 = 0	x1 = -5; x2 = ; x3 =
x4 – 12x2 +16x = 0	x1 = 0; x2 = -4; x3 = 2 (doble)

• Las ecuaciones bicuadradas son ecuaciones incompletas de cuarto grado sin términos de grado impar:

ax4 + bx2 + c = 0.   Para resolverlas, efectuamos el cambio x2 = y, y, por tanto, x4 = y2, con lo que queda una ecuación de segundo grado en la incógnita y:  ay2 + by + c = 0

Por cada valor positivo de y habrá dos valores de x: x =

Ej6 : Resolver las siguientes ecuaciones:

1. x4 - 10x2 + 9 = 0

2. x4 – 2 x2 – 3 = 0

3. x4 – 5x2 = 0

SISTEMAS DE ECUACIONES DE PRIMER GRADO (ecuaciones LINEALES)

Varias ecuaciones dadas conjuntamente con el fin de determinar la solución o las soluciones comunes a todas elllas forman un sistema de ecuaciones.

Sistema de ecuaciones con varias incógnitas es, entonces, un conjunto de ecuaciones que deben verificarse, cumplirse, para los mismos valores de las incógnitas.

Un sistema puede estar constituido por cualquier número de ecuaciones, de cualquier grado, cada una de las cuales puede tener cualquier número de incógnitas. Por ahora, veremos el caso más sencillo, el de un sistema de dos ecuaciones de primer grado con dos incógnitas.

Si las ecuaciones del sistema tienen dos incógnitas, representan rectas en el plano. Resolver el sistema es encontrar el punto en común que tienen todas las rectas, encontrar el punto en el que se cortan las rectas. (Una ecuación lineal con dos incógnitas representa una recta)

Si las ecuaciones del sistema tienen tres incógnitas, representan planos en el espacio. Resolver el sistema es encontrar el punto o los puntos que tienen en común todos los planos, encontrar la recta en la que se cortan los tres planos. (Una ecuación lineal con tres incógnitas representa un plano en el espacio)

RESOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES DE DOS INCÓGNITAS

• Método de sustitución (Despejamos una de las incógnitas en una ecuación y la sustituimos en la otra,)

Ej: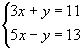  

15. Resuelve: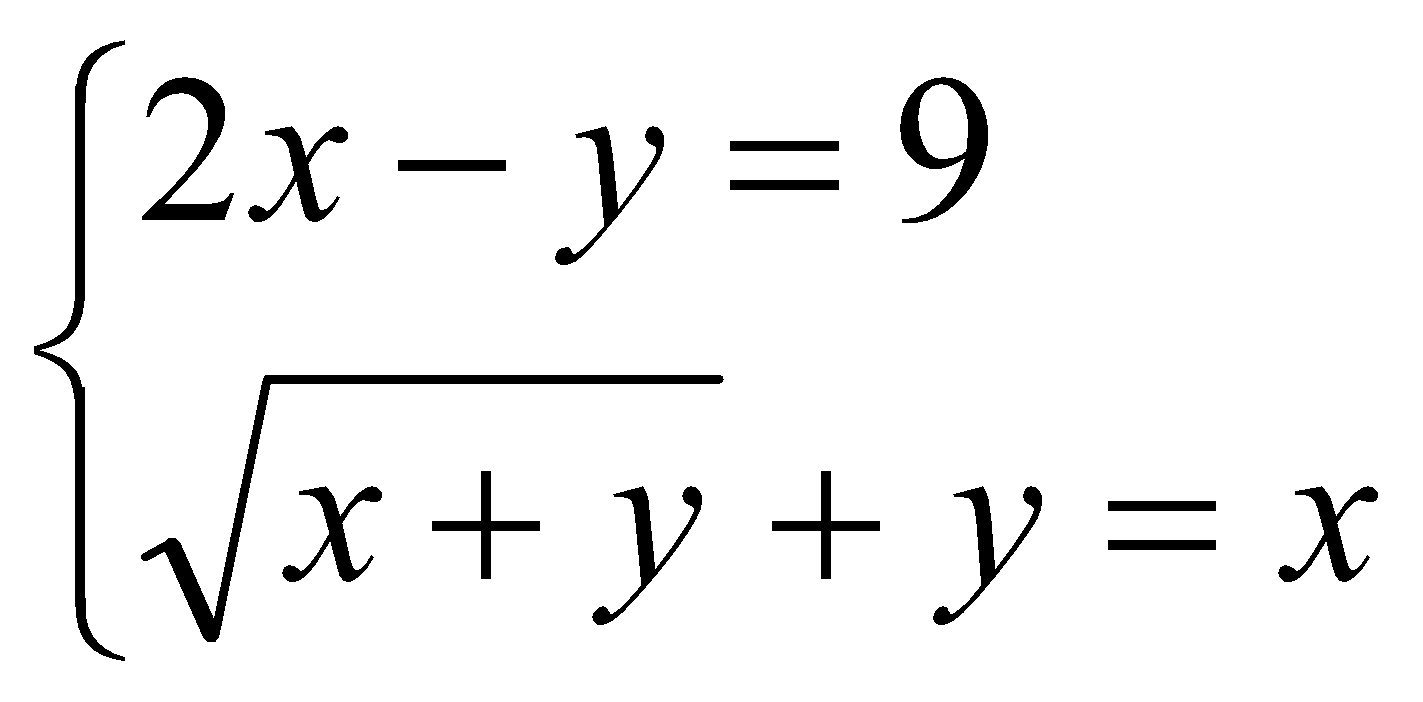

Sol:  x = 6,   y= 3 (COMPROBAR que las otras soluciones no pueden ser)

• Método de reducción (reducimos, eliminamos una de las incógnitas,…)

16. Resuelve:

Sol:  x =3     y = 2

• Método de igualación   (Despejamos la misma incógnita en ambas ecuaciones e igualamos,…)

17. Resuelve:

18. Resuelve por el método de reducción:

Sol:   x = 3/7     y= -12/7

19. Resuelve por el método de reducción:

20. Resuelve por el método de reducción:

21. Sobre una mesa hay latas de tónica y cola, en número total de 10. Si se duplica el número de latas de cola existentes, hay 14 latas en total. ¿Cuántas latas hay de cada clase?

22. En un pequeño zoo que sólo tiene jirafas y canguros, el guarda contó sólo cabezas y su hijo sólo patas. Había 92 cabezas y 290 patas (humanos no incluídos). ¿Cuántas jirafas hay?

23. Laura compró 30 sellos, algunos de 20 céntimos y otros de 30 céntimos, con un coste total de 750 céntimos. ¿Cuántos sellos de 20 céntimos compró?

24. Un ordenador y una impresora cuestan 660. El ordenador vale 360 euros más que la impresora. ¿Cuál es el precio de cada uno de los aparatos?

TRANSFORMACIONES VÁLIDAS EN UN SISTEMA DE ECUACIONES

Algunas de estas transformaciones ya las hemos realizado en los sistemas de ecuaciones lineales de dos incógnitas.

1. Multiplicar o dividir los dos miembros de una de las ecuaciones por un número distinto de cero.

2. Añadir una ecuación que sea combinación lineal de las demás o, al contrario, suprimir una ecuación que sea combinación lineal de las otras.

3. Sustituir una ecuación por el resultado de sumarle otra multiplicada por un número.

4. Cambiar el orden de las ecuaciones.

Estas transformaciones nos permiten transformar un sistema de ecuaciones en otro sistema equivalente que tiene las misma soluciones y que es más fácil de resolver.

Se llaman transformaciones válidas a las que mantienen las soluciones del sistema.

En la resolución de sistemas de ecuaciones debemos realizar transformaciones que, además de válidas, sean convenientes, es decir, que nos aproximen a la solución. Para ello utilizaremos, fundamentalmente, las transformaciones 1 y 3 descritas. (En realidad, ya lo hemos hecho en la resolución de sistemas de dos incógnitas utilizando el método de reducción)

SISTEMA DE ECUACIONES ESCALONADO

Un sistema de tres ecuaciones con tres incógnitas se llama escalonado si en una de las ecuaciones solo aparece una sóla incógnita; en otra de las ecuaciones falta alguna de las otras dos incógnitas, y en la ecuación que queda tenemos todas las incógnitas. Estos sistemas escalanados son muy fáciles de resolver.Por ej., resuelve:

 =  

25. Reconoce como escalonado y resuelve:  

26. Resuelve:   

27. Resuelve:

MÉTODO GAUSS para la resolución de sistemas de ecuaciones

El método de Gauss para la resolución de sistemas de ecuacions consiste en transformar un sistema de ecuaciones lineales en otro escalonado. Para ello hacemos ceros sometiendo las ecuaciones a dos transformaciones elementales:

• Multiplicar o dividir una ecuación por un número distinto de cero.

• Sumar, o restar, a una ecuación otra multiplicada por un número.

• Cambiar de orden las ecuaciones.

El proceso se realiza muy ventajosamente si, en lugar de las ecuaciones, utilizamos exclusivamente los números –coeficientes y términos independientes- estructurados en matrices.

1º Colocamos los coeficientes.

2º Al aplicar Gauss obtenemos el sistema escalonado (“preparando” previamente las ecuaciones del sistema) de tal manera que tengamos ceros bajo la diagonal principal. (La primera ecuación, con coeficiente 1 para la x, permanecerá invariable).

3º Si nos da una contradicción (por ej.: 0 = 8) El sistema es incompatible, es decir, no tiene solución. (Los planos no se cortan en ningún punto ni recta común)

4º Si se nos anula toda una ecuación, nos quedan menos ecuaciones que incógnitas, el sistema es compatible indeterminado y tiene infinitas soluciones dependientes de una de las incógnitas. (Los planos se cortan en una línea, como las páginas de un libro, por ejemplo)

5º Si tiene una única solución el sistema es compatible determinado. (Todos los planos se cortan en un único punto común)

28. Resuelve:

a)  

b)

c)

d)

e)

# f)

29. Un cajero automático contiene 95 billetes de 10, 20 y 50 euros y un total de 2000 euros. Si el número de billetes de 10 € es el doble que el número de billetes de 20 €, averigua cuántos billetes hay de cada tipo.

30. Se dispone de tres cajas A, B y C con monedas de 1 euro. Se sabe que en total hay 36 euros. El número de monedas de A excede en 2 a la suma de las monedas de las otras dos cajas. Si se traslada 1 moneda de la caja B a la caja A, esta tendrá el doble de monedas que B. Averigua cuántas monedas había en la caja.

31. Un fabricante produce 42 electrodomésticos. La fábrica abastece a 3 tiendas, que demandan toda la producción. En una cierta semana, la primera tienda solicitó tantas unidades como la segunda y tercera juntas, mientras que la segunda tienda pidió un 20% más que la suma de la mitad de lo pedido por la primera más la tercera parte de lo pedido por la tercera. ¿Qué cantidad solicitó cada una?

#32. En cierta heladería, por una copa de la casa, dos horchatas y cuatro batidos te cobran 34 € un día. Otro día, por cuatro copas de la casa y cuatro horchatas te cobran 44 € y, un tercer día, te piden 26 € por una horchata y cuatro batidos. ¿Tienes motivos para pensar que alguno de los tres días te han presentado una cuenta incorrecta?

33. Una empresa dispone de 27200 € para actividades de formación de sus cien empleados. Después de estudiar las necesidades de los empleados, se ha decidido organizar tres cursos, A, B y C. La subvención por persona para el curso A es de 400 €, para el curso B es de 160 €, y de 200 € para el C. Si la cantidad que se dedica al curso A es cinco veces mayor que la correspondiente al B, ¿cuántos empleados siguen cada curso?

TEORÍA. ECUACIONES LINEALES

Una ecuación lineal es una ecuación polinómica de grado uno con una o varias incógnitas (x, y, z, …).

Una ecuación lineal con dos incógnitas representa una recta en el plano. Los puntos de la recta son las soluciones de la ecuación.

Una ecuación lineal con tres incógnitas representa un plano en el espacio. Los puntos del plano son las soluciones de la ecuación.

Dos ecuaciones son equivalentes cuando tienen la misma solución (o las mismas soluciones).

Si a dos miembros de una ecuación los multiplicamos o dividimos por un mismo número distinto de cero., la ecuación resultante es equivalente a la primera.

SISTEMAS DE ECUACIONES LINEALES

Varias ecuaciones dadas conjuntamente con el fin de determinar la solución o las soluciones comunes a todas ellas forman un sistema de ecuaciones.

Si las ecuaciones del sistema tienen tres incógnitas, representan planos. Resolver el sistema es encontrar el punto o los puntos que tienen en común todos los planos.

Dos sistemas de ecuaciones son equivalentes si tienen las mismas soluciones.

Dos sistemas pueden ser equivalentes sin que lo sean las ecuaciones que los forman,  por tanto,  puede no ser evidente que los sistemas sean equivalentes (en numerosas ocasiones “aparentan” no serlo).

TRANSFORMACIONES VÁLIDAS EN UN SISTEMA DE ECUACIONES

1. Multiplicar o dividir los dos miembros de una de las ecuaciones por un número distinto de cero.

2. Añadir una ecuación que sea combinación lineal de las demás o, al contrario, suprimir una ecuación que sea combinación lineal de las otras.

3. Sustituir una ecuación por el resultado de sumarle otra multiplicada por un número.

4. Cambiar el orden de las ecuaciones.

Se llaman transformaciones válidas a las que mantienen las soluciones del sistema.

En la resolución de sistemas de ecuaciones debemos realizar transformaciones que, además de válidas, sean convenientes, es decir, que nos aproximen a la solución. Para ello utilizaremos, fundamentalmente, las transformaciones 1 y 3 descritas.

SISTEMAS DE ECUACIONES CON SOLUCIÓN Y SIN SOLUCIÓN

• Un sistema de ecuaciones puede tener solución (compatible) o no tener solución (incompatible).

• Los sistemas compatibles pueden tener una solución (determinados) o infinitas soluciones (indeterminados).

Interpretación geométrica de sistemas de ecuaciones con DOS INCÓGNITAS

Un sistema de ecuaciones lineales con dos incógnitas representa un conjunto de rectas. Su resolución consiste en averiguar si todas ellas tienen un punto en común y localizarlo.

Si un sistema de ecuaciones tiene una única solución (x = a, y = b), es COMPATIBLE y significa que las rectas determinadas por las ecuaciones pasan por el mismo punto (x = a, y = b). En este caso el número de incógnitas y de ecuaciones independientes coinciden.

Si un sistema de ecuaciones carece de solución (al intentar resolverlo, llegamos a expresiones disparatadas, contradictorias, por ejemplo 5 =8, ó 0z = 20) entonces, las ecuaciones son incompatibles. En este caso no existe ningún punto en común entre las rectas determinadas por las ecuaciones (porque son paralelas o no se cortan todas en el mismo punto).

Interpretación geométrica de sistemas de ecuaciones con TRES INCÓGNITAS

Sistema compatible determinado: Los tres planos determinados por las tres ecuaciones se cortan en el mismo punto. Solución única. En este caso el número de incógnitas y de ecuaciones independientes coinciden.

Sistema compatible indeterminado: Los planos se cortan a lo largo de un plano; entonces, todos los puntos de la recta donde se cortan los planos son solución del sistema. Existen, por tanto, infinitas soluciones. En este caso, el número de incógnitas del sistema es mayor que el de ecuaciones independientes.

Sistema incompatible: No todos los planos se cortan ni en el mismo punto ni en la misma recta. No existe, por tanto, solución para el sistema. En este caso encontramos resultados absurdos, incongruentes, imposibles como, por ejemplo, 0z = 5. (Ejemplos realizados: ej29 f de página 16, ej 32 de página 18,…)