EL NÚMERO REAL. CONJUNTO R.
Hasta ahora hemos visto que toda fracción se puede expresar como número decimal; sin embargo el recíproco no es cierto: no todo número decimal se puede expresar como fracción (los decimales infinitos no periódicos, 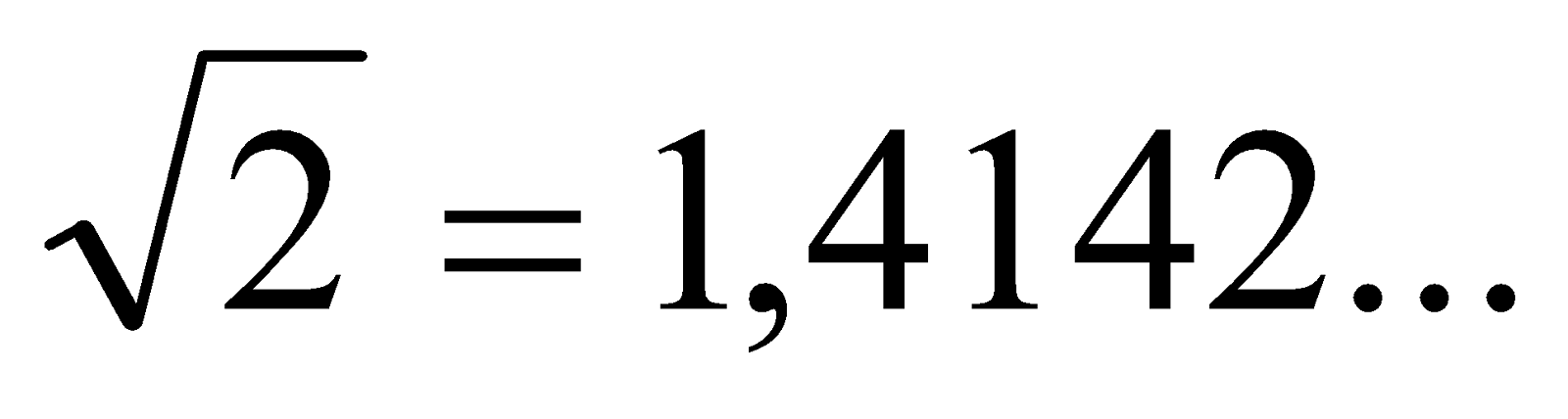 ; ó el número
; ó el número  (pi); ó el número
(pi); ó el número  (fi); ó el número e,…). Estos números decimales ni exactos ni periódicos, son los números irracionales (conjunto I) que pueden definirse como los números decimales infinitos no periódicos.
(fi); ó el número e,…). Estos números decimales ni exactos ni periódicos, son los números irracionales (conjunto I) que pueden definirse como los números decimales infinitos no periódicos.
El conjunto de los números reales, R, está formado por la unión de los números racionales y los números irracionales. 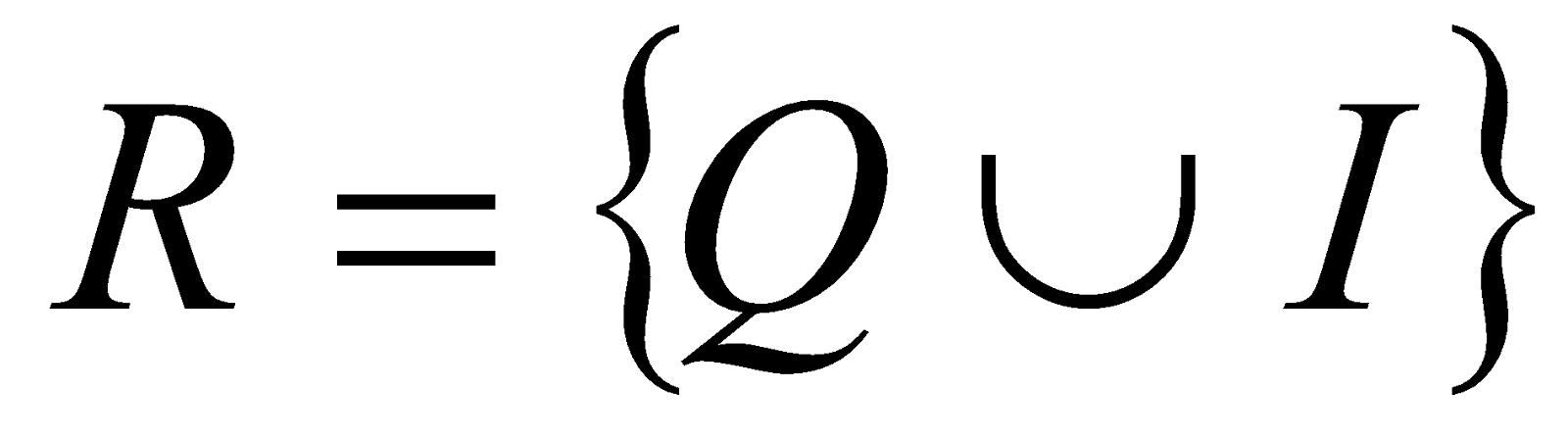
Los números reales se representan como puntos en una recta llamada recta real.
POTENCIAS DE BASE ENTERA Y EXPONENTE NATURAL
Potencia de base a (número entero) y exponente n (número natural) es el producto de n factores iguales al número a:
an = a · a · a ·…  a1 = a
a1 = a
Ej.: (-2)4 = (-2) · (-2) · (-2) · (-2) = + 16
(-4)3 = (-4) · (-4) · (-4) = -64
Signo de una potencia
Si la base es positiva……………………………siempre positiva
Si la base es negativa
25 =
(-2)2 =
(-2)3 =
-24 =
-23 =
Operaciones con potencias
am · an = am+n 33 · 32 = ; 35 · 3-2 =
(am)n = am · n (73)2 = ; (7-3)2 = ; (7-3)-2 = ; 
(a · b · c)n = an · bn · cn
a0 = 1 (recuerda: a es un número entero, es decir, positivo, 0 ó negativo)
Potencias con exponente negativo
Una potencia con exponente negativo es igual a la unidad dividida por la misma potencia de exponente positivo, y viceversa.
a-n =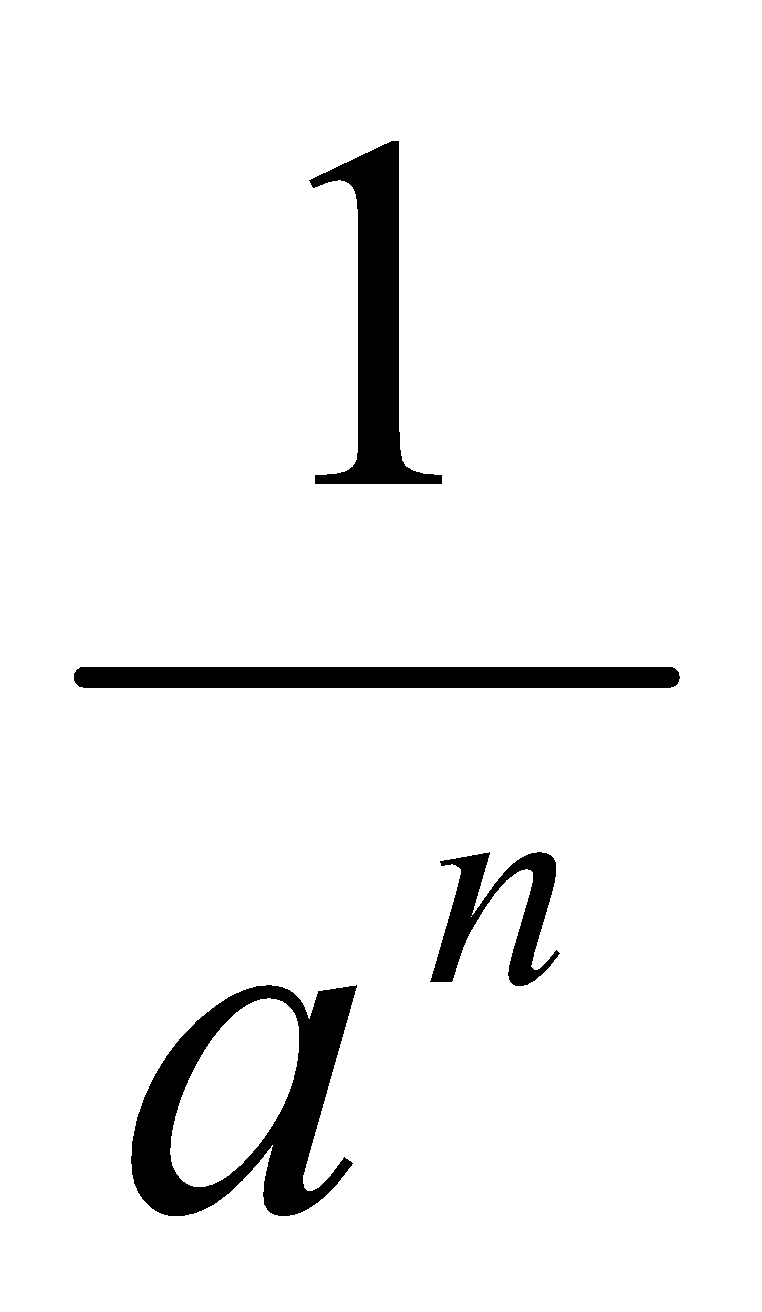 2-3 =
2-3 =
- Escribe en forma de potencia:
4 · 4 · 4 · 4 · 4 = 12 · 12 · 12 · 12 · 12 · 12 · 12 =
(-5) · (-5) · (-5) · (-5) = 10 · 10 · 10 · 10 · 10 =
- Escribe en forma de producto:
42 = 71 = 164 = (-2)3 =
(-7)6 = 130 = -36 =
-55 = 3-2 = (-6)-3 =
- Calcula en forma de potencia:
24 · 23 = 37 · 34 = 37 : 34 = 46 · 40 = 199 : 194 =
- Sustituye el signo de interrogación por el exponente que falta:
(25)? = 215 (4?)2 = 48 3? · 39 = 310 5 · 5 = 5? 5? · 59 = 5 12
4? · 45 = 45 2? · 21 = 2 (25)? = 2-15 (4?)-2 = 48 (5?)? = 550
- Simplifica estas operaciones:
a4 · a3 = a7 : a2 =  (a2)4 =
(a2)4 =
- Escribe el resultado como potencia única:
(-3)4 · (-3)2 · (-3) = 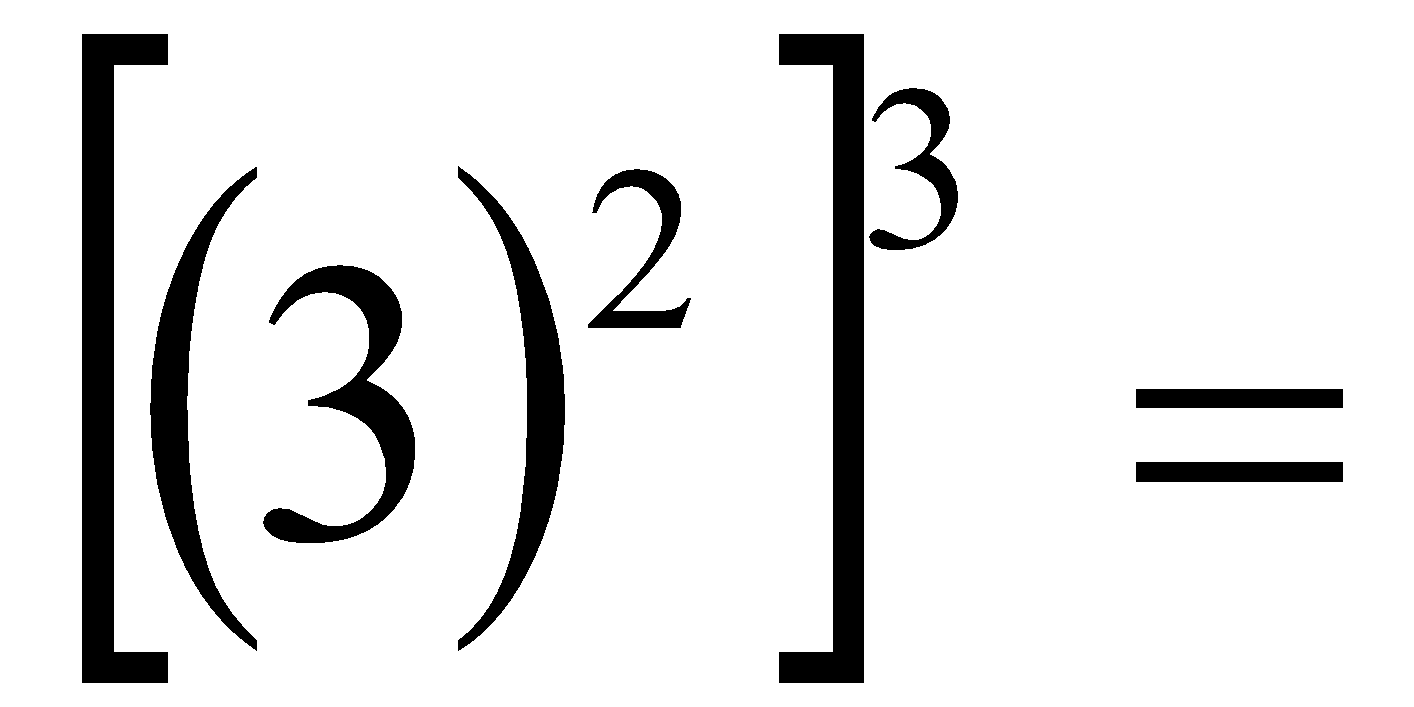

- Escribe el resultado como potencia única.
(-7)5 : (-7)3 = 48 · 4-3 = 48 · 43 =
(-25)9 : (-25)4 = (-25)9 · (-25)-4 = 39 : 36 =
(73 · 53 · 133)0 = (5 · 53 · 50 · 54)3 = 74 · 77 · 7 · 70 =
- Calcula y simplifica:
(-5)3 = (-5)2= (-5)7 · (5)3 =
-53 = -52 = 98 · 92 =
78 · 7-2 = 78 : 7-2 = 7-8 · 7-2 =
34 · 35 = 35 · (-34) = 54 · 510 =
(-25) · (28) =  = (-35)8 =
= (-35)8 =
- Descompón en factores y simplifica
Números irracionales. Radicales
Llamamos raíz n-ésima de un número real a, a otro número b (si existe) que elevado a la potencia n nos da a.
Raíz de a :  donde
donde 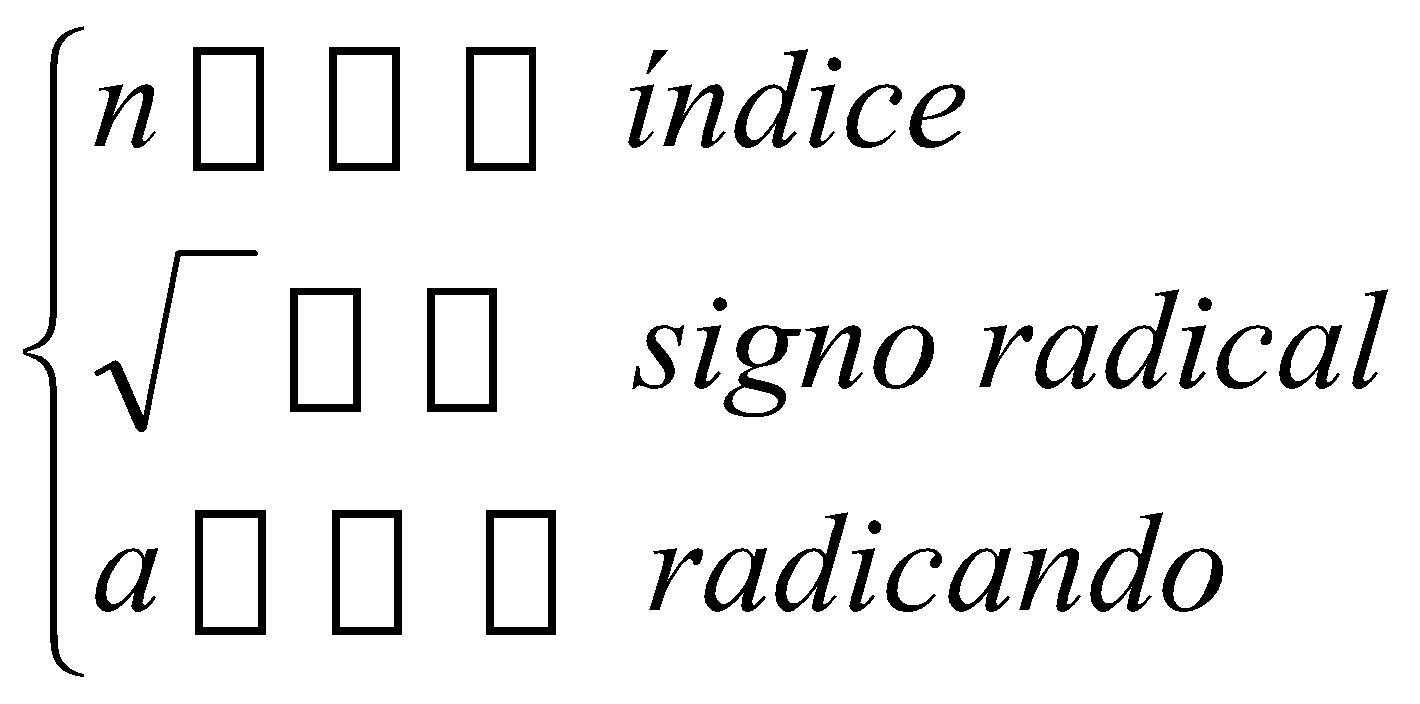 tal que bn = a;
tal que bn = a;  , entonces 32 = 9
, entonces 32 = 9
Relación entre potencias y radicales
a)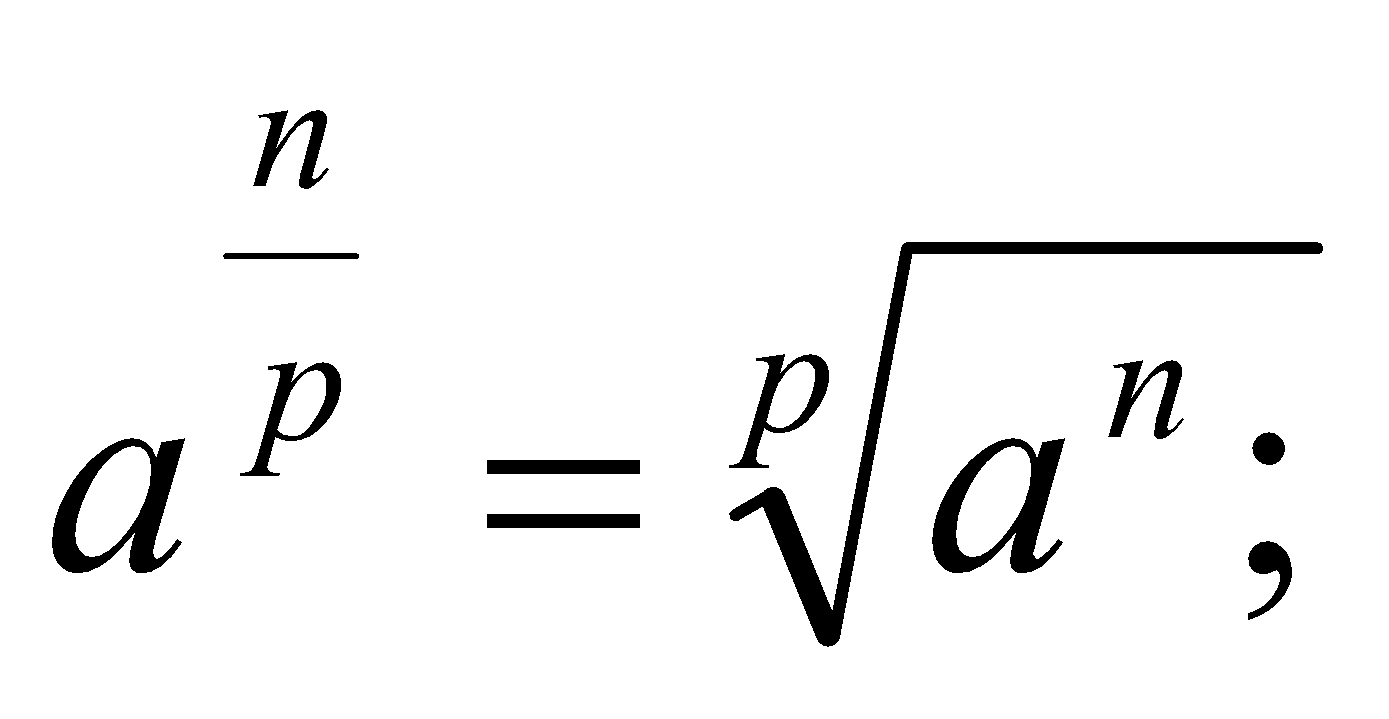

b) 

Propiedad fundamental de los radicales
El valor de un radical no varía si se multiplican o se dividen por un mismo número el exponente y el índice del mismo.
Transformación de radicales
Un radical puede transformarse, de infinitas formas, en otro, multiplicando o dividiendo el exponente y el índice del radicando por un mismo número.
Reducción de radicales a índice común
1º Se halla el m.c.m. de los índices, que será el índice común.
2º Se divide el índice común por cada índice original y, los cocientes resultantes se multiplican respectivamente por cada exponente de los radicandos.
Reducir a índice común: 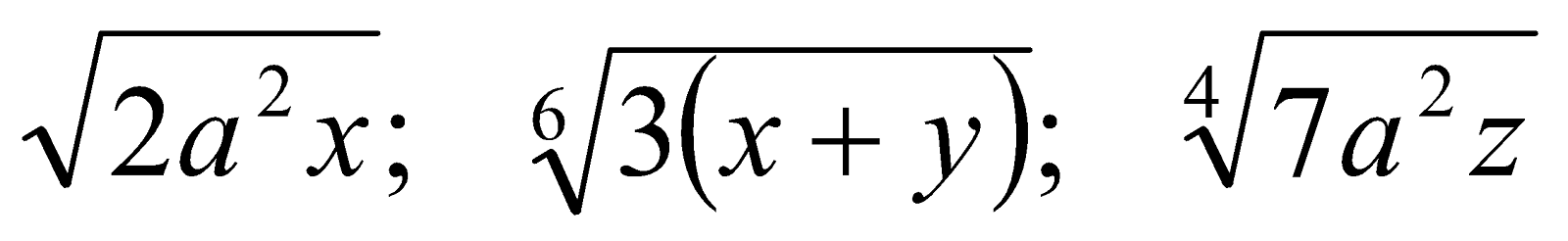
Raíz de un producto:
Raíz de un cociente:
Potencia de una raíz: se eleva el radicando a la potencia dada (al exponente dado).
Raíz de una potencia: Se obtiene la raíz de la base y se eleva el resultado a la potencia dada.
Ej.:  o, también:
o, también: 
Raíz de una raíz:
Extracción de raíces de índice compuesto:
Ejemplo:  ó:
ó: 
Extracción de factores de un radical:
Es necesario que el índice sea igual o menor que el exponente del factor. Se divide el exponente entre el índice, y el cociente sale como exponente de dicho factor fuera de la raíz y el resto queda como exponente dentro de la raíz. (Si los factores son números hay que descomponerlos previamente en factores primos).
Ejemplo: 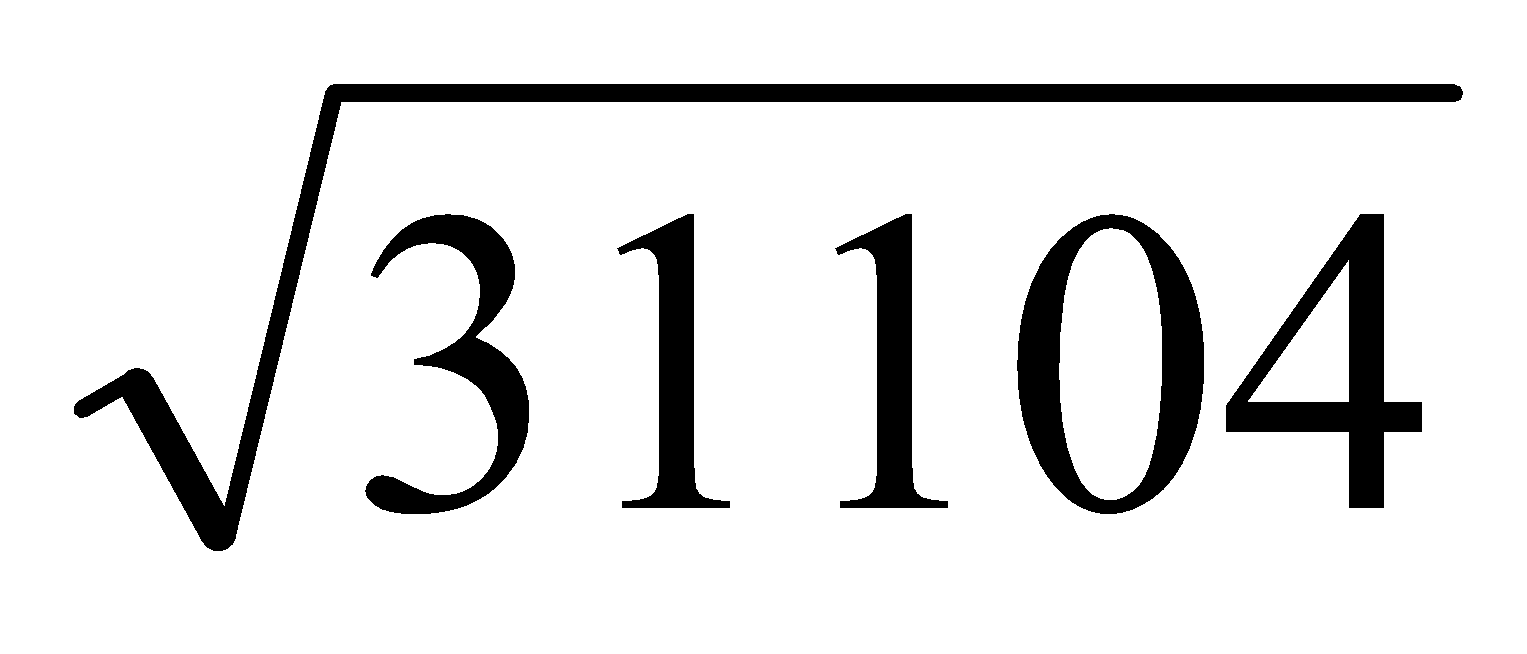 1º Descomponer el número en factores:
1º Descomponer el número en factores:
=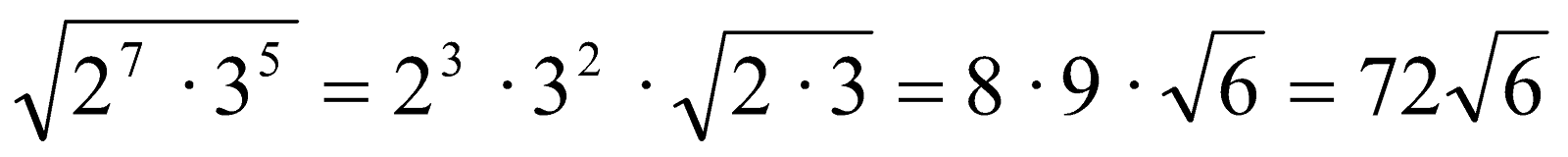
Introducción de factores en un radical:
Para introducir factores dentro de una raíz hay que elevar dichos factores al índice de la raíz.
Radicales semejantes:
Radicales semejantes son aquellos que tienen el mismo índice y el mismo radicando. Pueden diferir únicamente en el coeficiente.
Ej.:  son radicales semejantes.
son radicales semejantes.
Suma y resta de radicales
Solo se pueden sumar o restar radicales semejantes. Para proceder se saca el radical como factor común de la suma algebraica de los coeficientes.
Ej.: 
Multiplicación y división de radicales
Si los radicales tienen el mismo índice: se multiplican o dividen los radicandos y se le coloca al resultado de la raíz el mismo índice:
Si los radicales tienen distinto índice, se reducen previamente al índice común:
Racionalización de denominadores:
Esta operación consiste en eliminar raíces de un denominador, convirtiéndolo en un número entero. Hay varios casos:
- El denominador es un monomio, en el que aparece una raíz cuadrada. Para racionalizar: se multiplican el numerador y el denominador por la raíz que aparece en el denominador. Es conveniente simplificar antes los radicales, si ha lugar.
Ej.: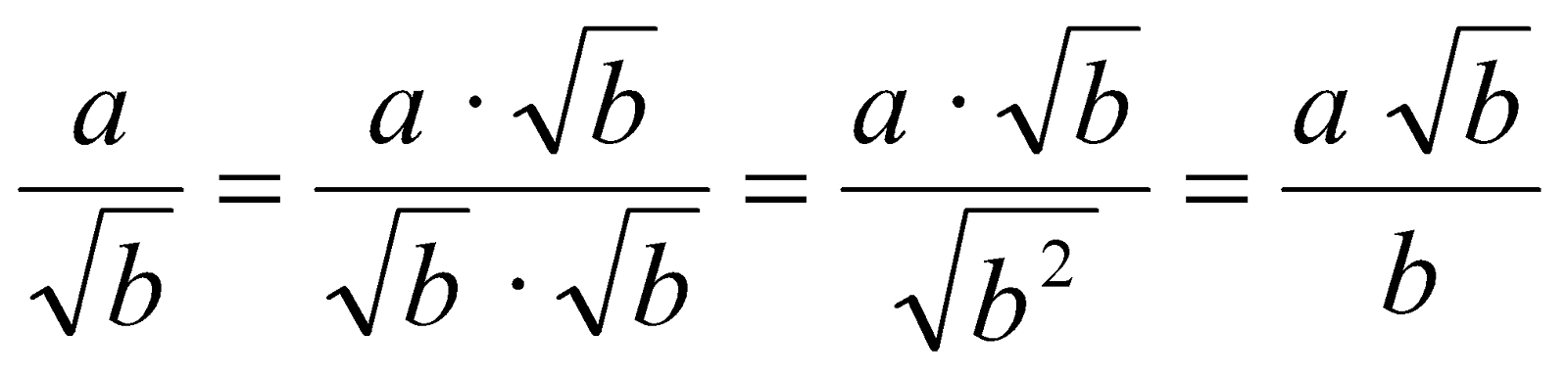
- El denominador es una raíz de índice cualquiera m o bien el radicando es una potencia. Se resuelve, en general, así: (multiplicando al numerador y al denominador por la raíz que completaría al denominador para extraer un número entero de la raíz)
- El denominador es un binomio. Se resuelve así: Se multiplican numerador y denominador por el conjugado del denominador( conjugado de un binomio se obtiene cambiando de signo el segundo término del binomio: conjugado de a + b es a – b; y el conjugado de a – b es …………………).
Ej.: 

Ejercicios:
Expresa el resultado mediante un solo radical y racionaliza:
Racionaliza:
Ejercicios:
a)  b)
b) 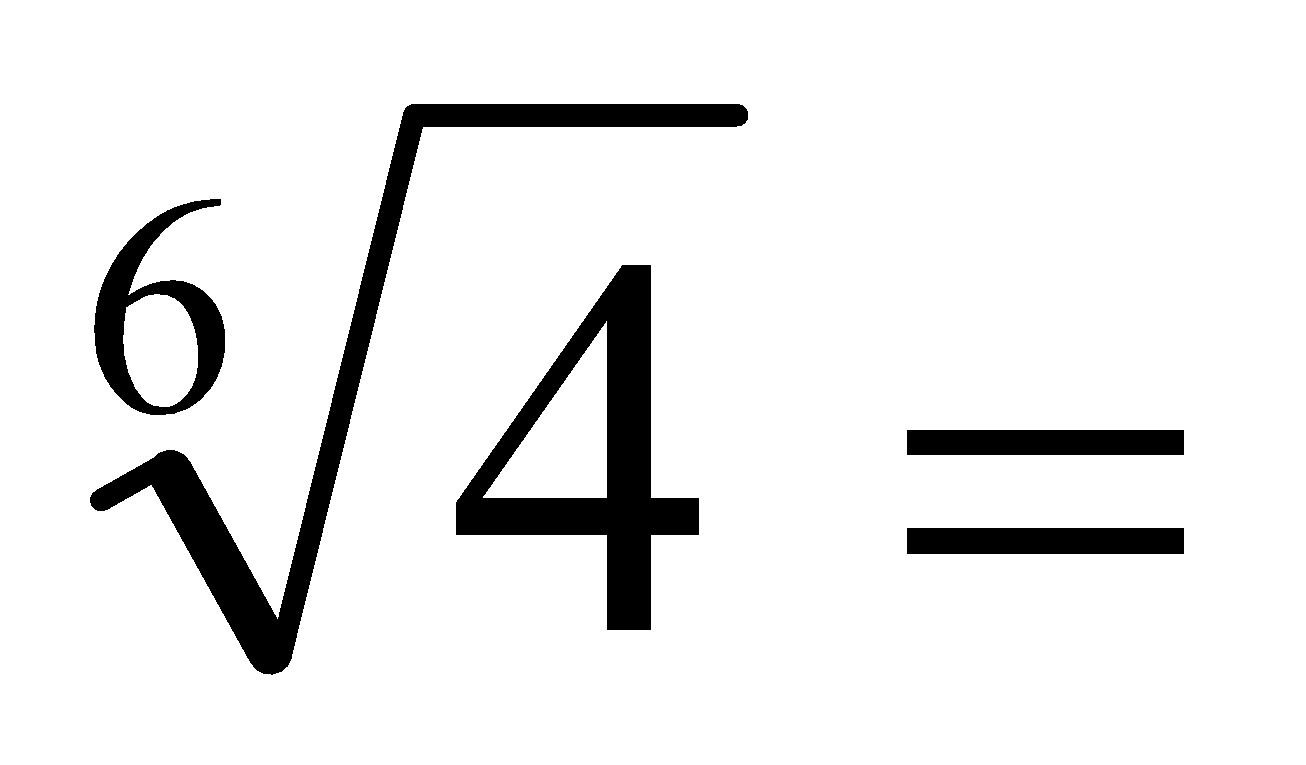 c)
c) 
d)  e)
e) 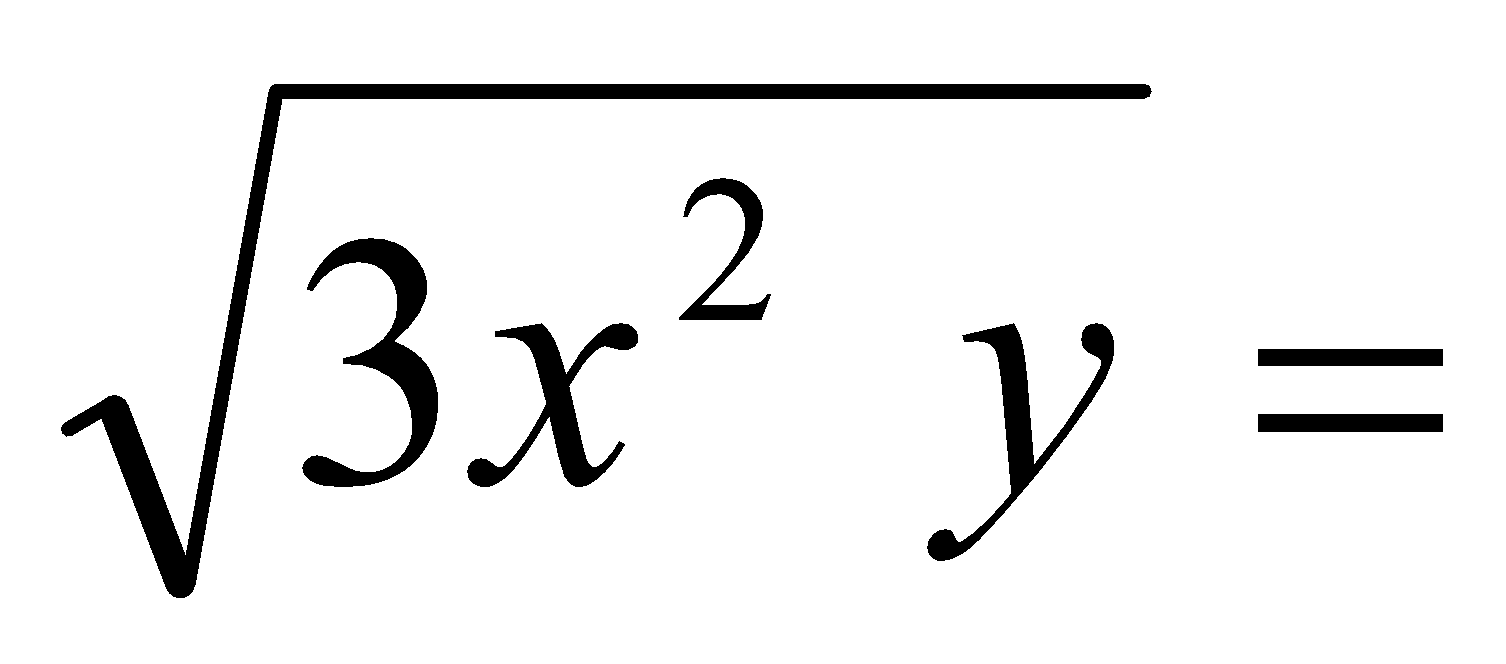 f)
f) 
g) 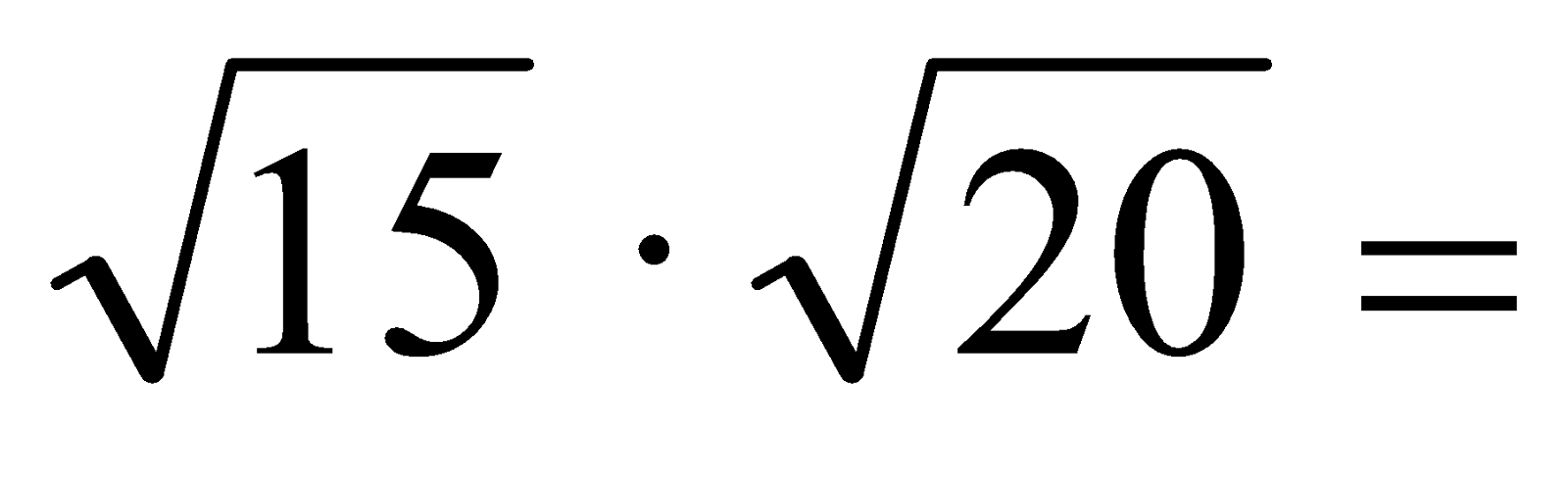 h)
h) 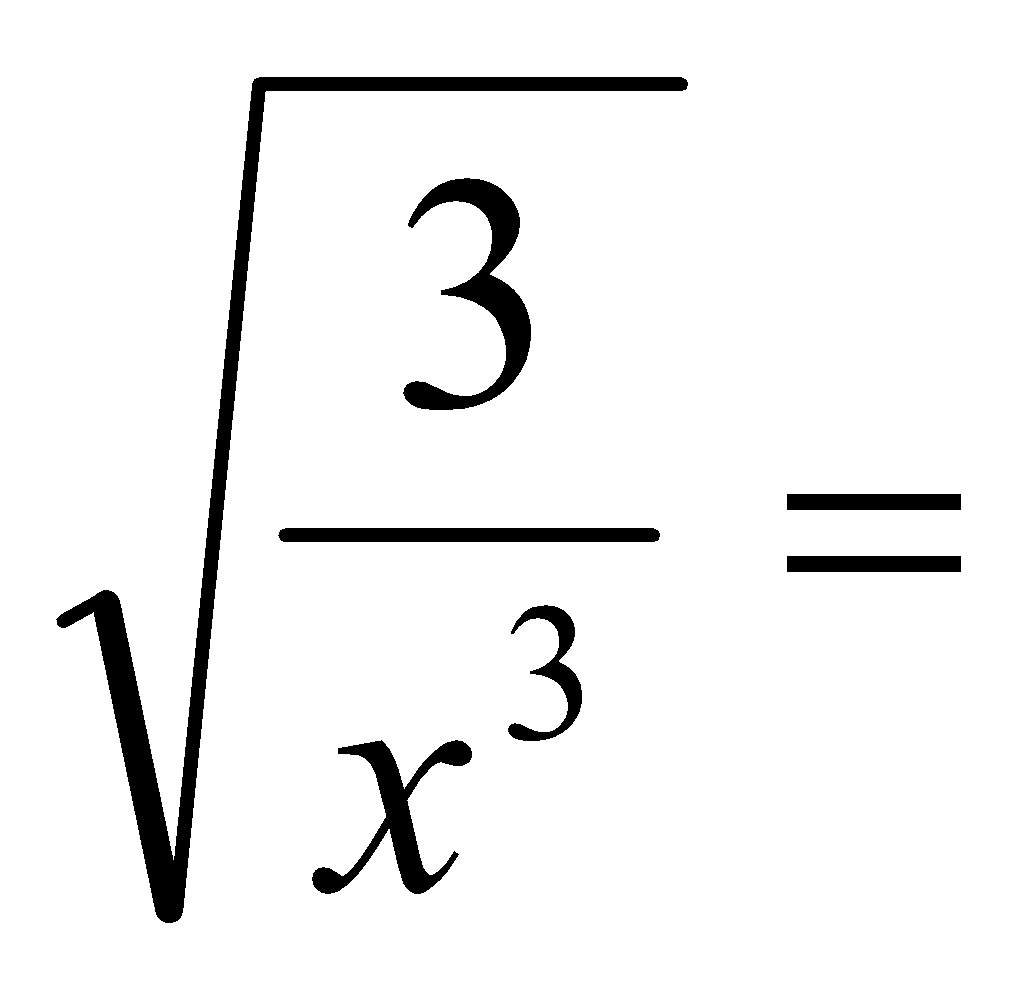
i)  j)
j) 
Razionaliza y simplifica:
a) 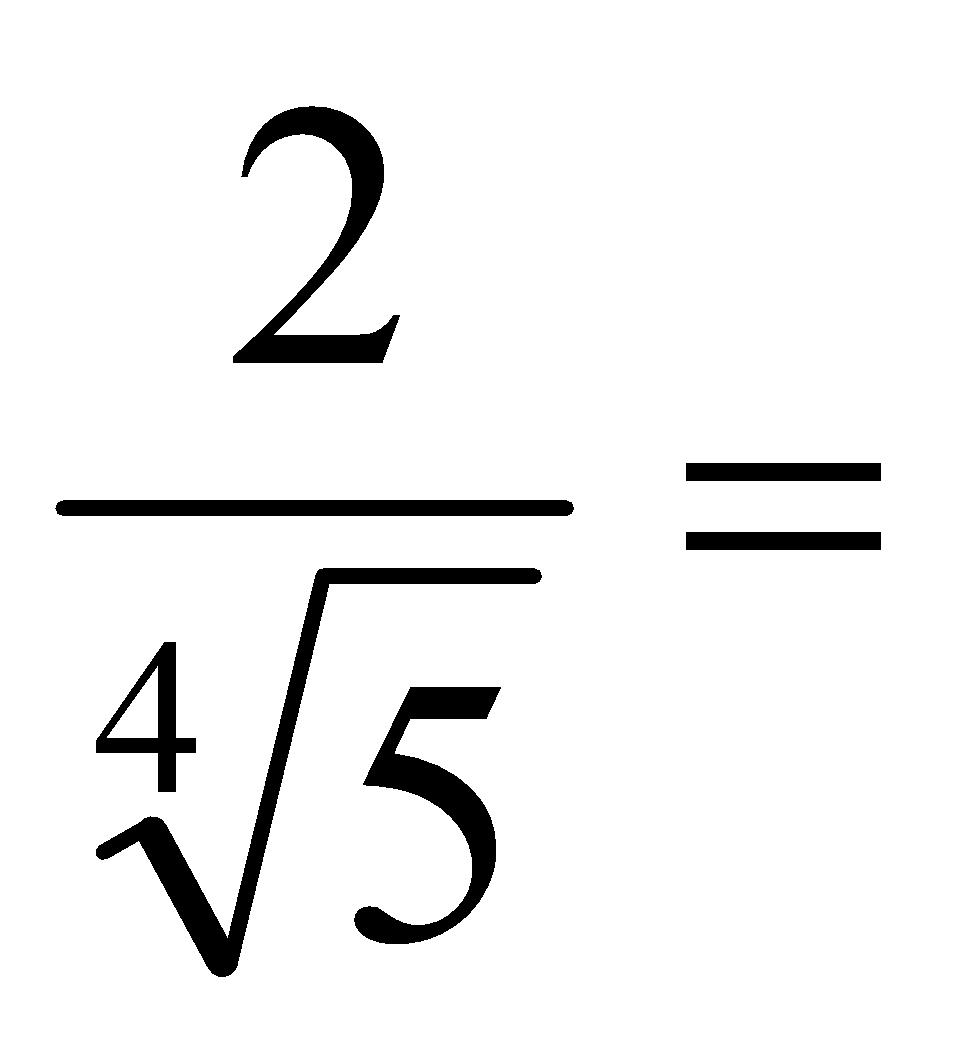
b) 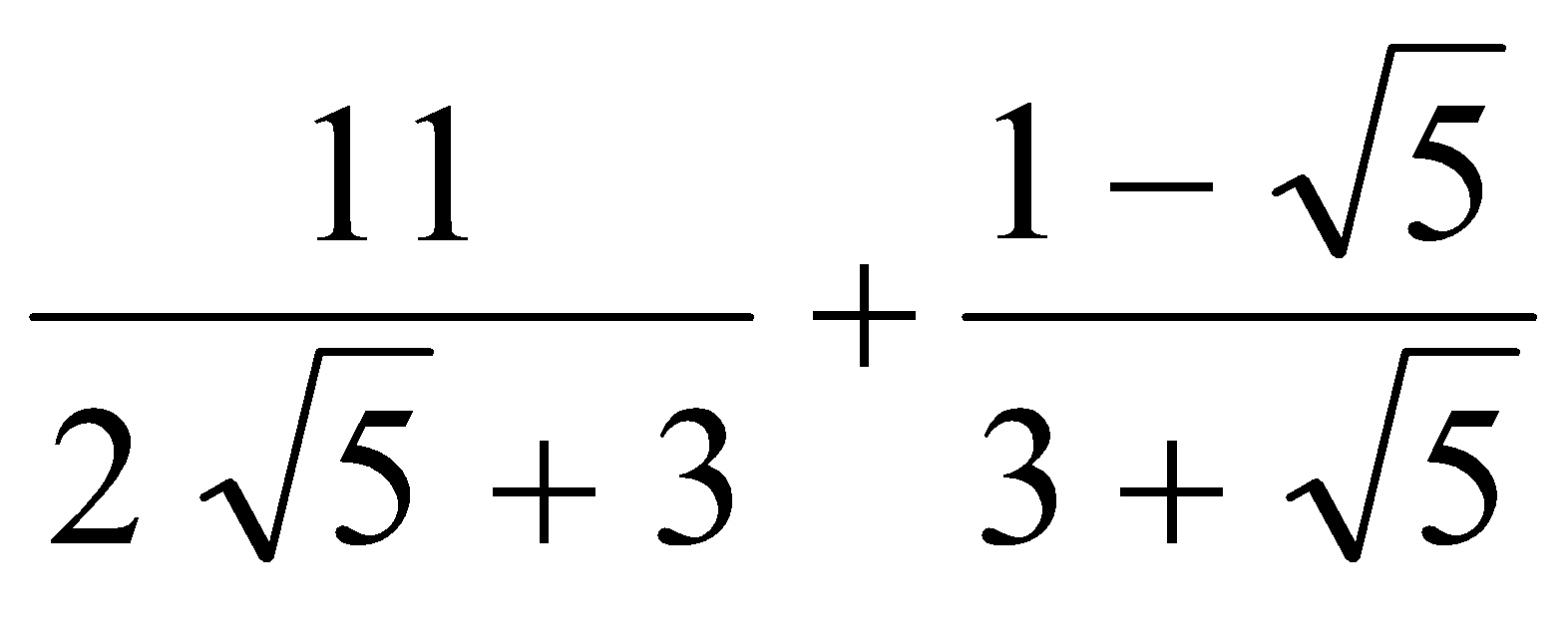
Efectúa las operaciones, simplifica y expresa en forma de potencia.
a) 
b) 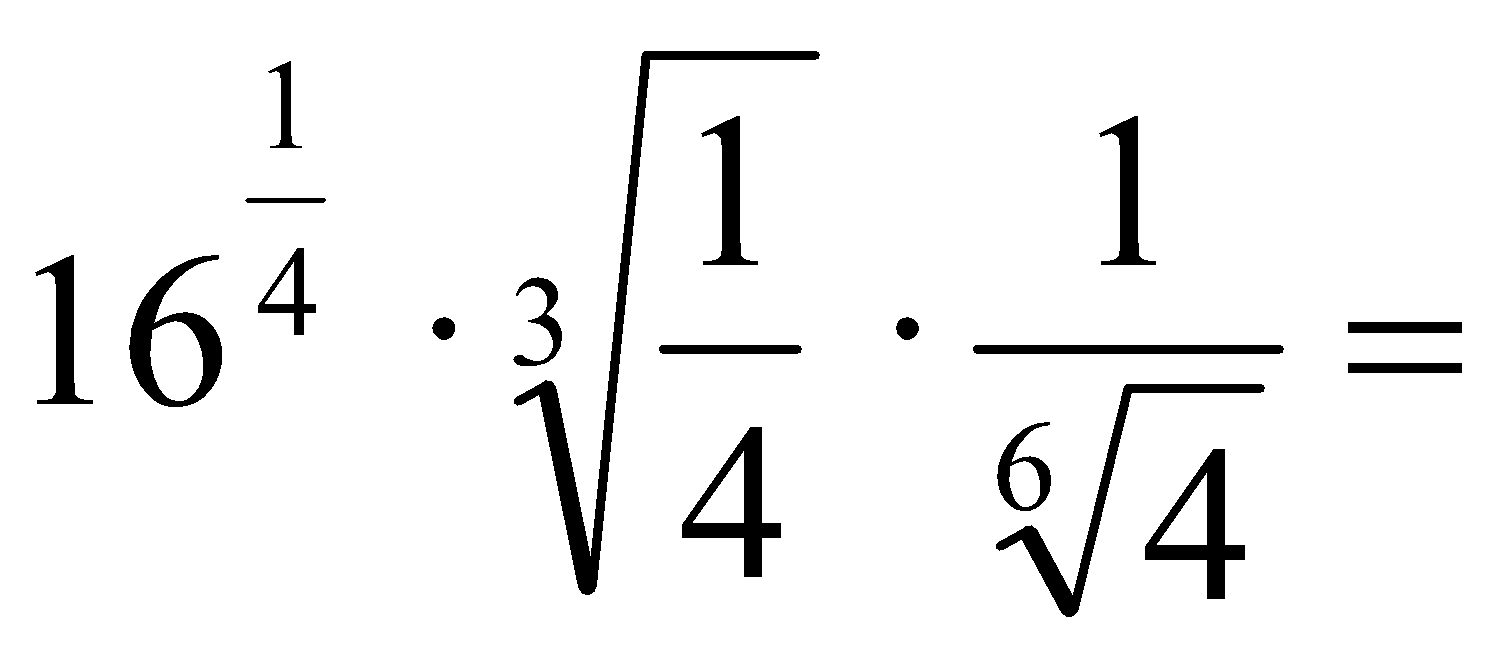
Simplifica:
a) 
b) 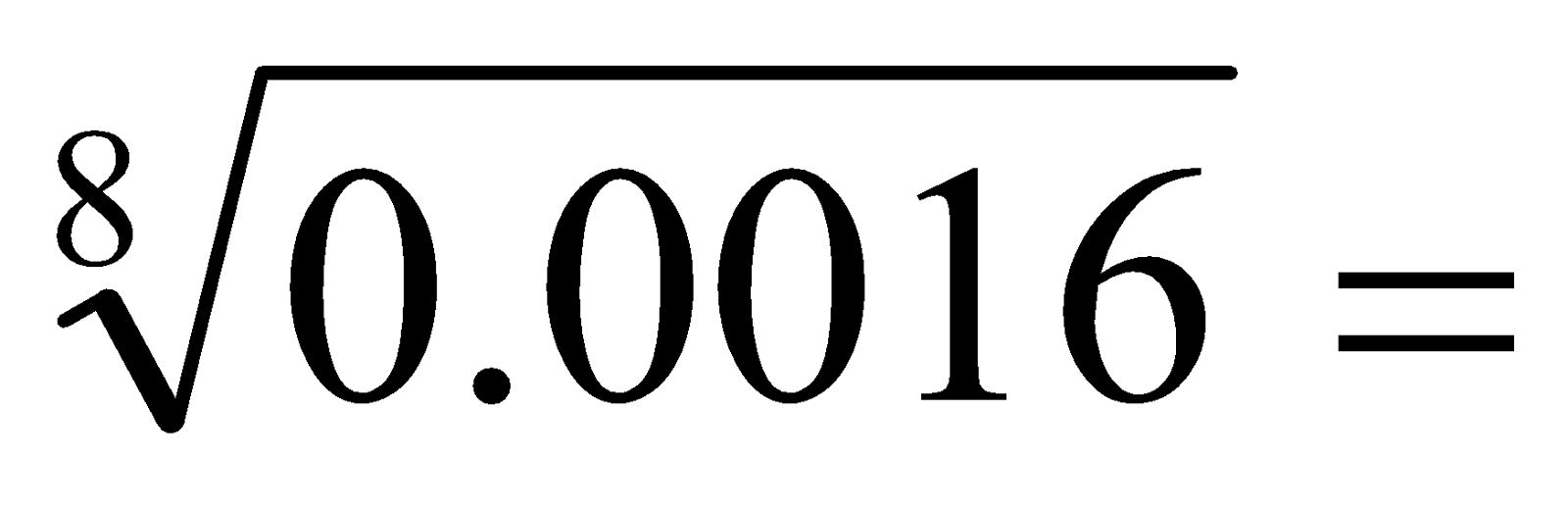
c) 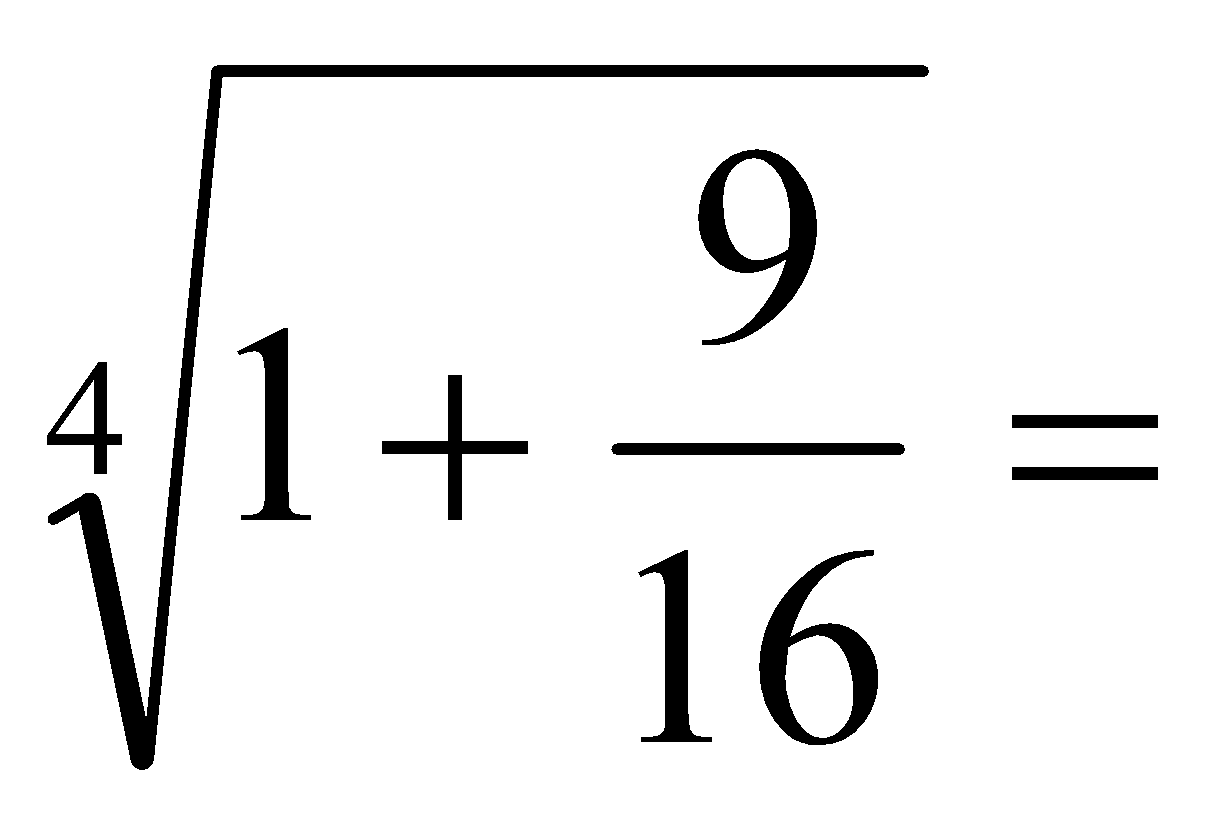
Simplifica:
a) 
b) 
c) 
d) 
e) 
f) 
Simplifica:
a) 
b) 
c) 
Racionaliza y simplifica:
a) 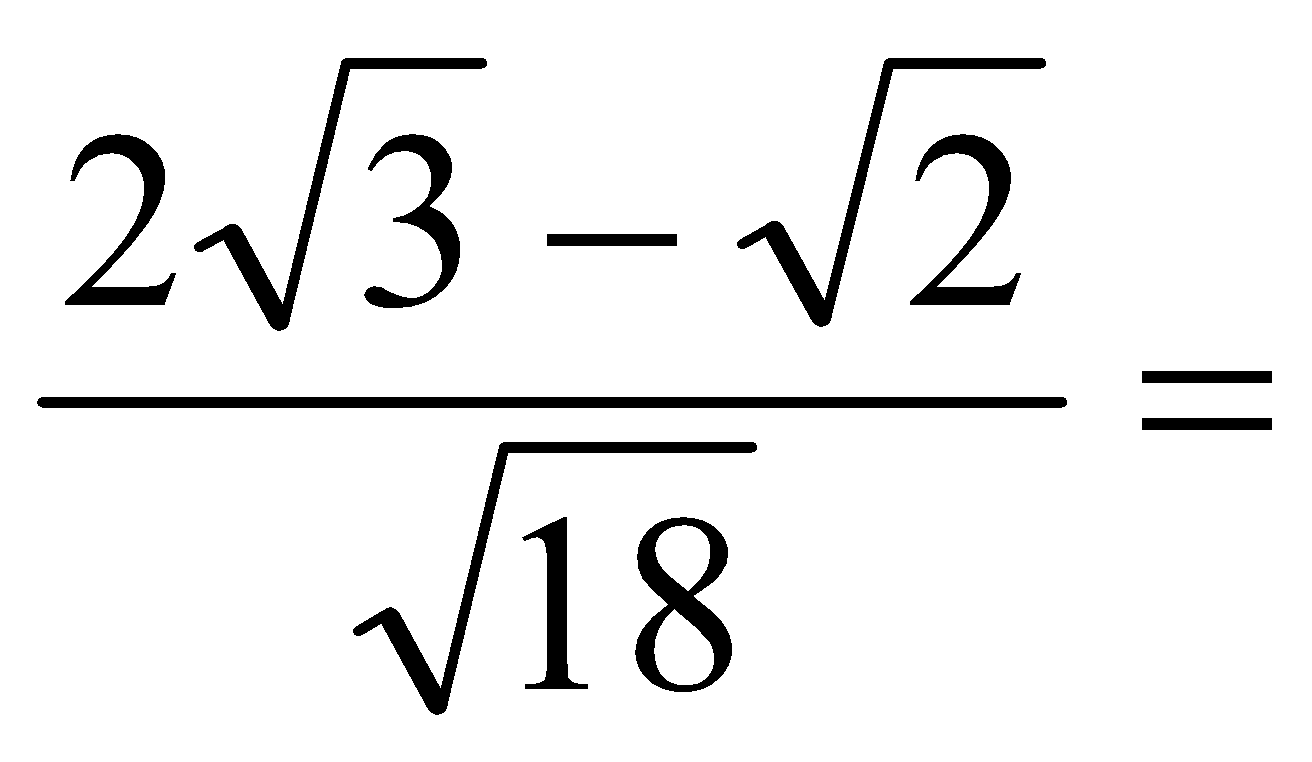
b) 
c) 
d) 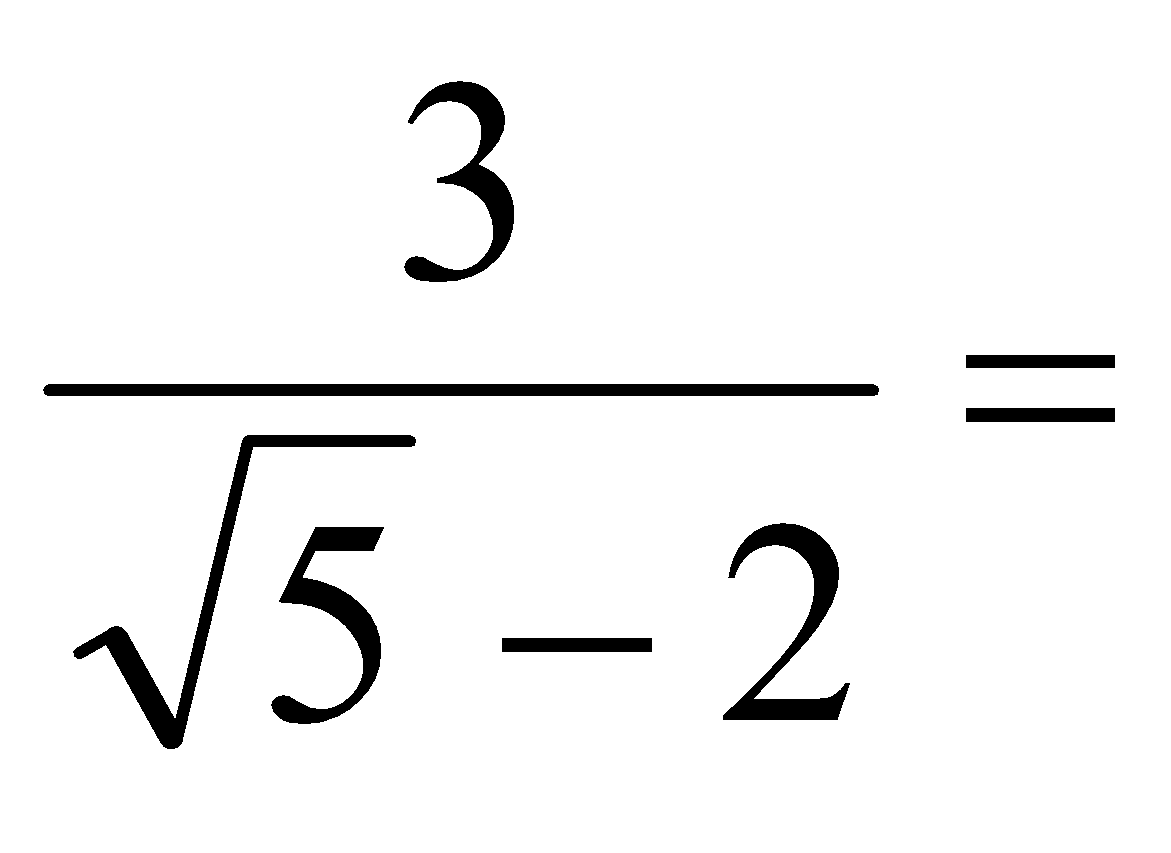
Racionaliza y efectúa:
a) 
b) 
¿Cuál es el resultado de?:
a) 
b) 
c) 
d) 
e)
f) (-4)2 = g) -42 = h) 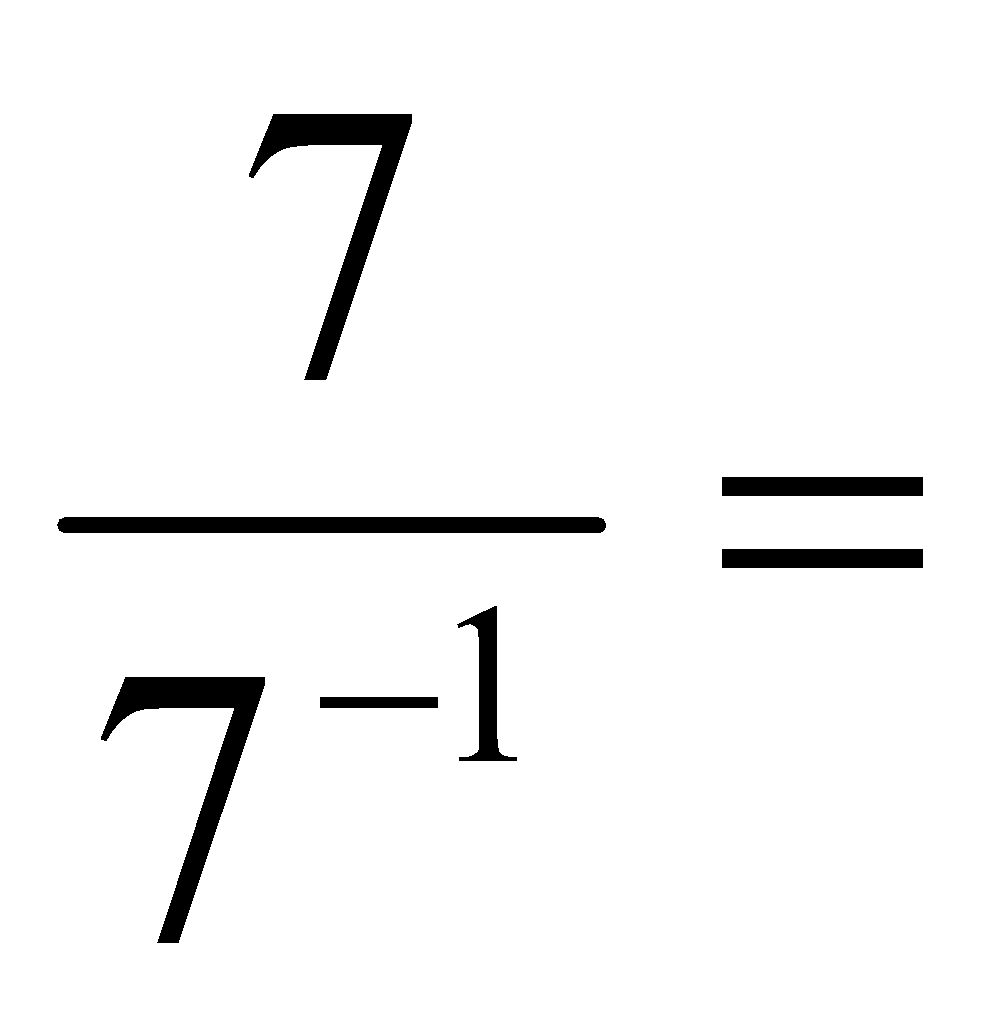
i) (-3)3 = j) (-3)4 = k) -32 =
l) 2-3 = m) 3-2 = n) 4-2 =
Calcula:
a) (2 · 3)2 = b) (2 · 3)-1 = c)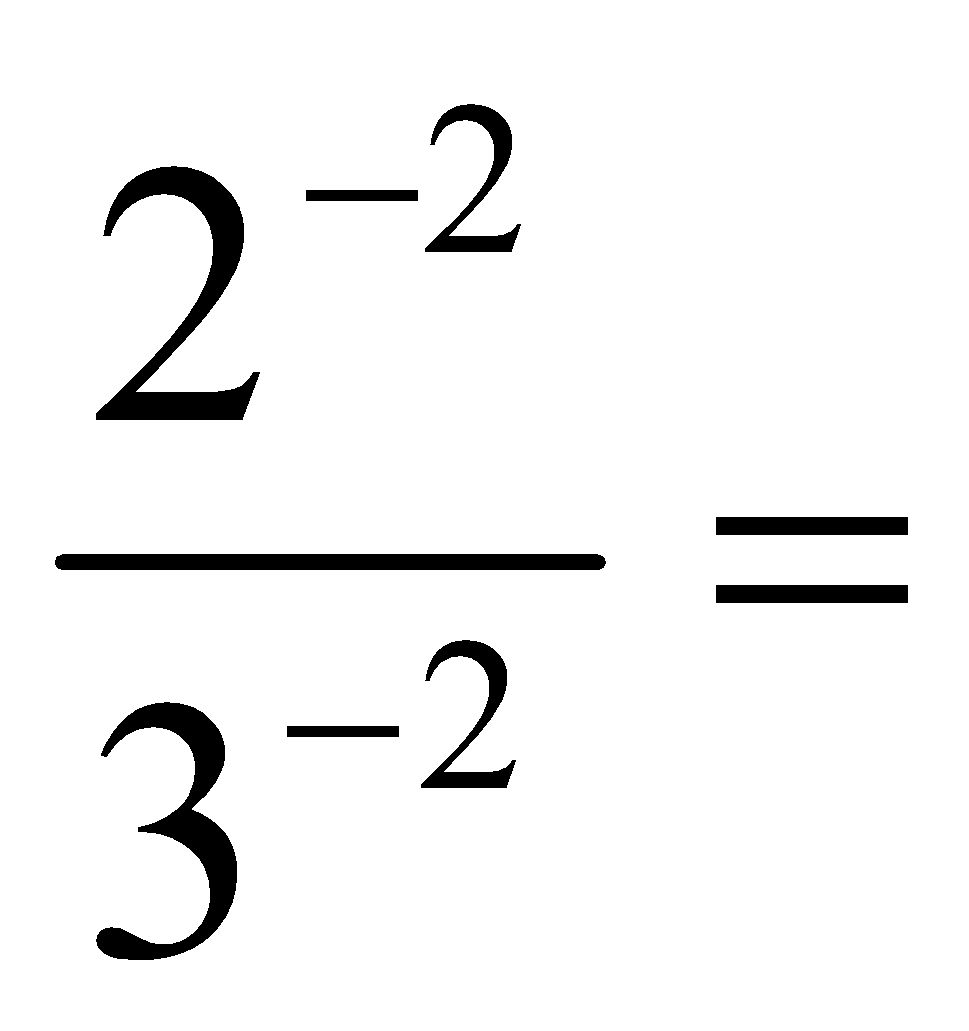
d) 
Transforma los siguientes radicales en potencias:
a)  b)
b) 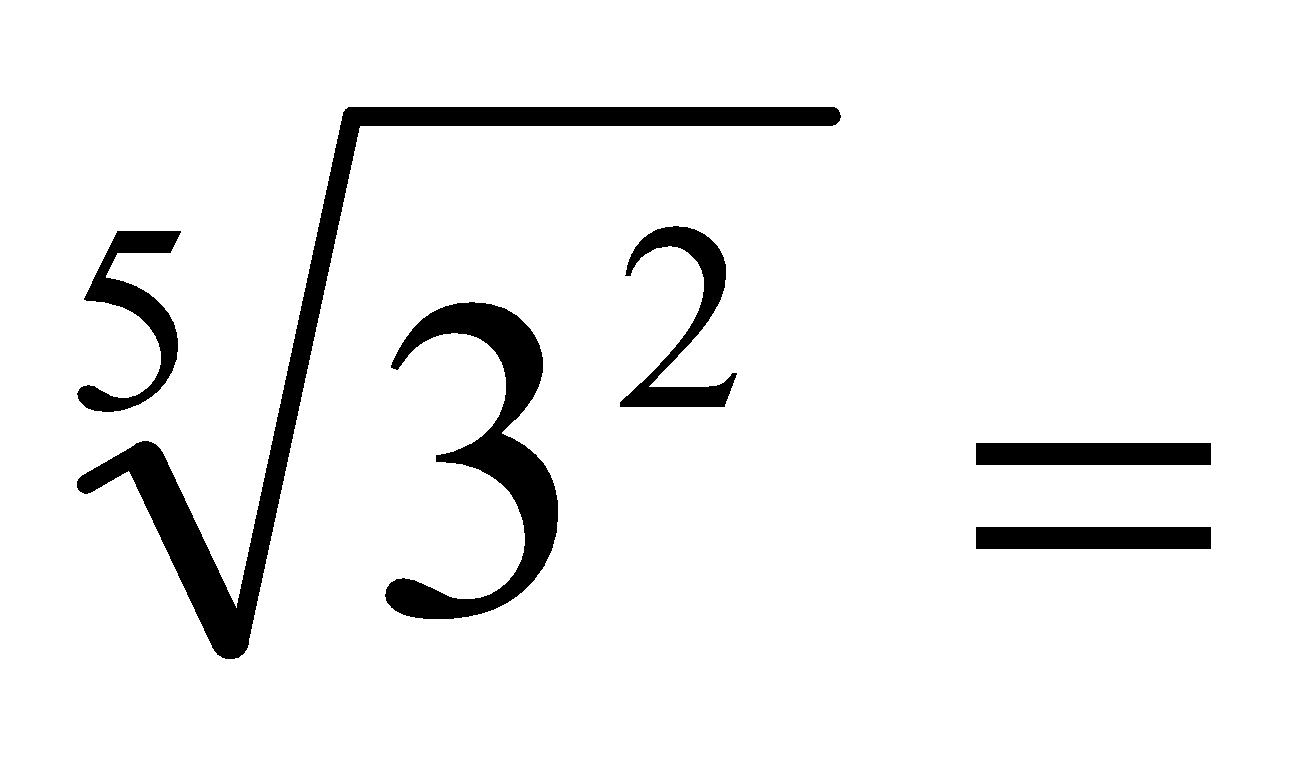
Transforma las siguientes potencias en radicales:
a)  b)
b) 
Racionaliza:
a) 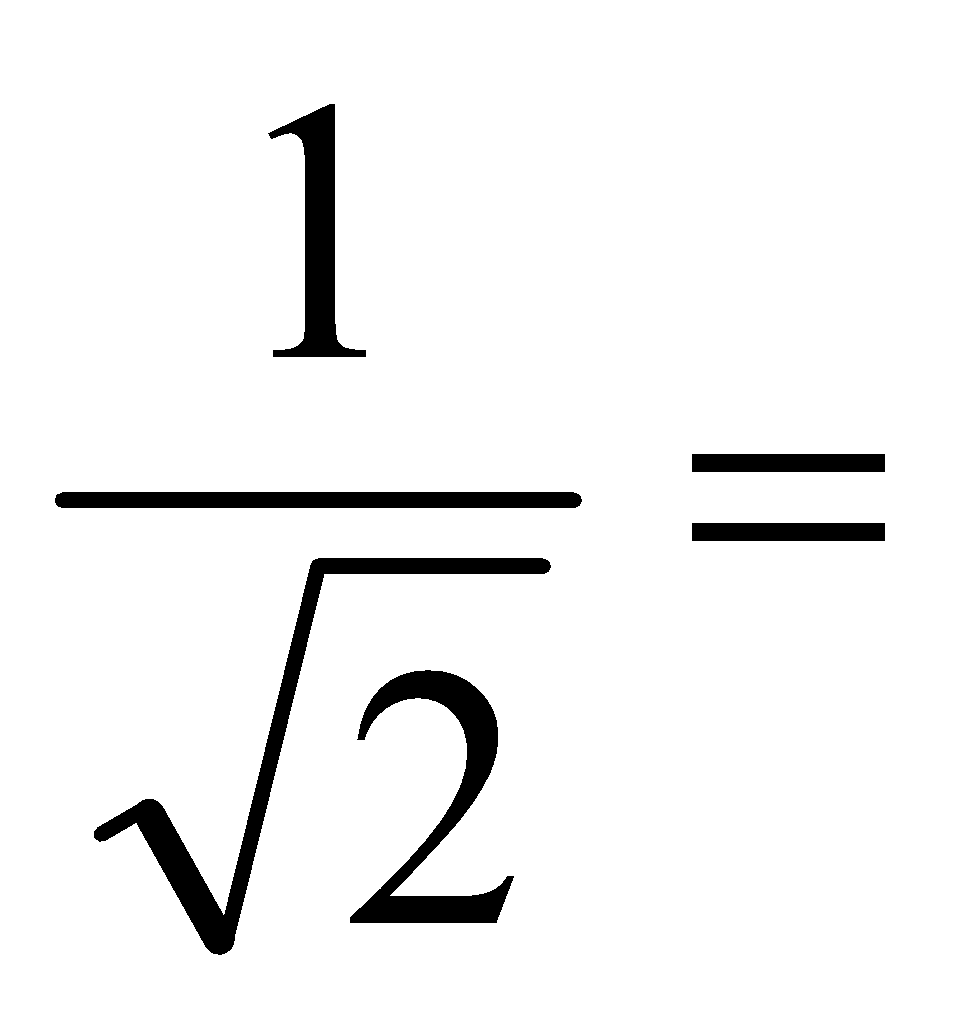 b)
b) 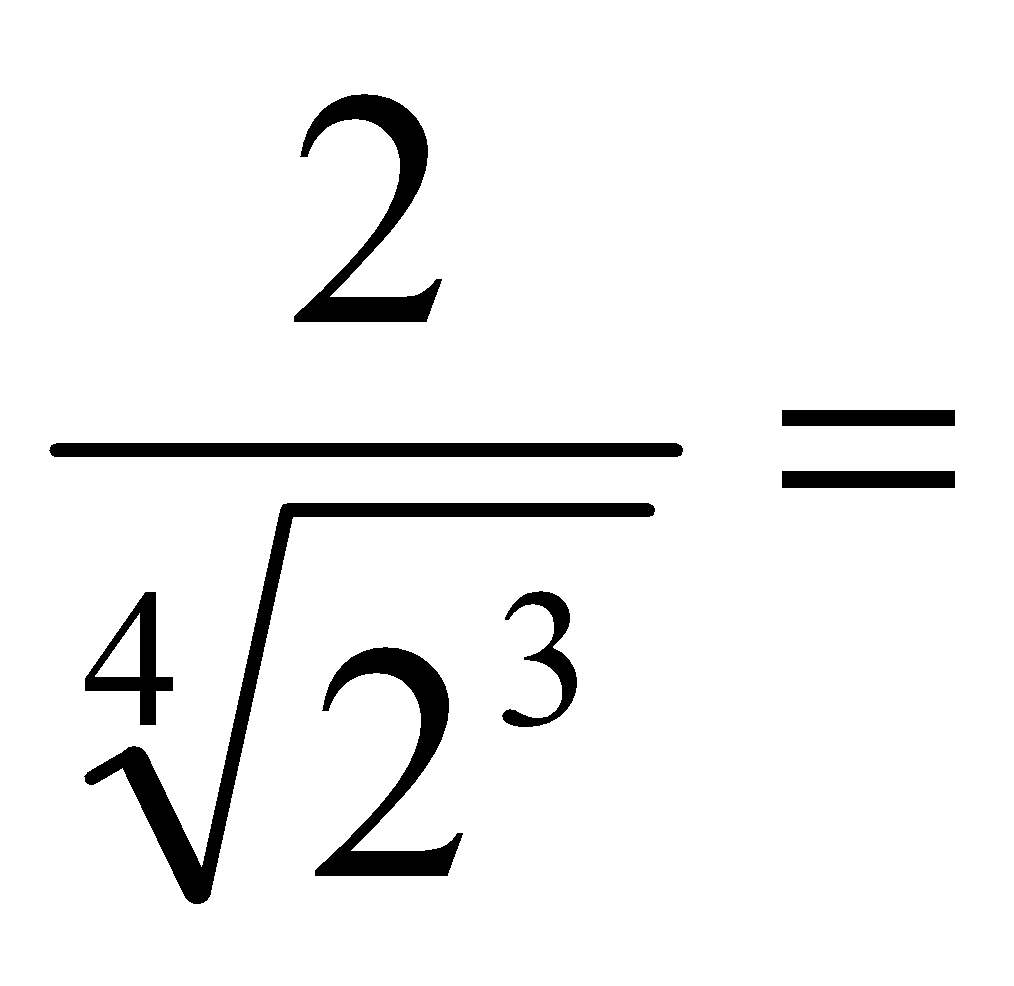
c) 
Resuelve las siguientes operaciones con radicales:
a)  b)
b) 
c)  d)
d) 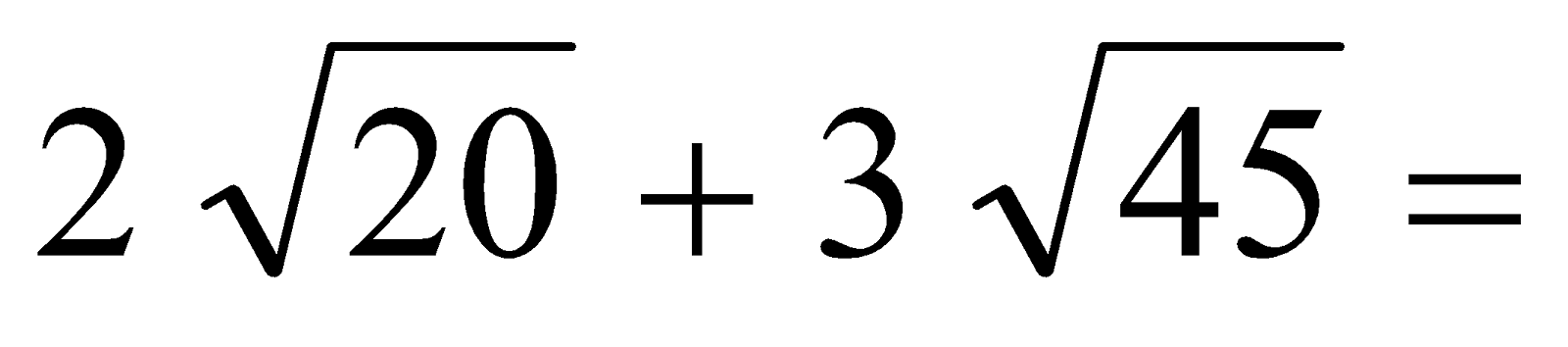
Calcula:
810.75 = 80.333… =
Extrae factores:
Introduce factores:
Poner a índice común:
Realiza las sumas:
a) 
b) 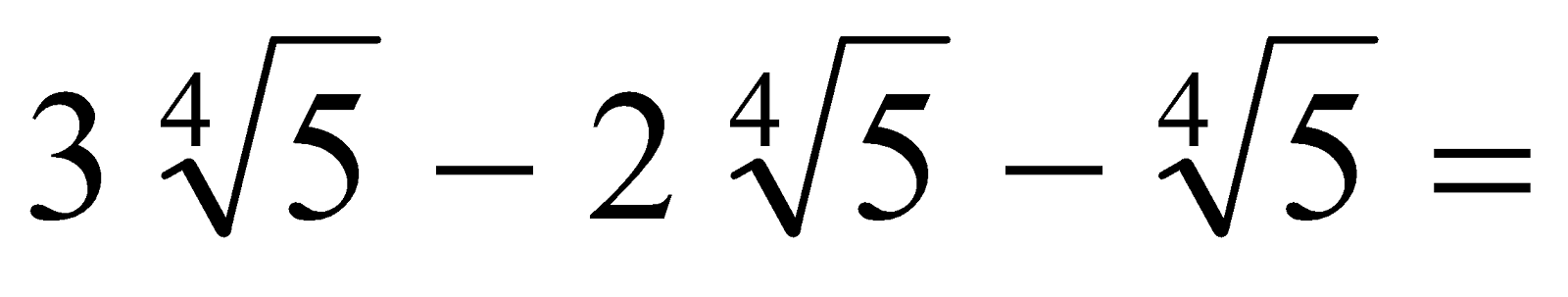
c) 
d)
Halla las siguientes sumas:
Efectúa las sumas.
Realiza los productos:
Efectúa las divisiones con los radicales:
Calcula:
Realiza las operaciones:
Efectúa:
Racionaliza:
Intervalos y semirrectas (en R)
- Intervalos de extremos a y b
Un intervalo es un segmento (un conjunto de puntos) de la recta real que tiene por extremos dichos puntos. Los intervalos pueden ser de cuatro tipos dependiendo de que se incluyan o no sus extremos:
Intervalo cerrado: contiene ambos extremos. Se representa por 
Intervalo abierto: No contiene ninguno de sus extremos. Se representa por 
Intervalo semiabierto por la izquierda: No contiene el extremo de la izquierda. Se representa por 
Intervalo semiabierto por la derecha: No contiene el extremo de la derecha. Se representa por 
- Semirrectas
Una semirrecta es un intervalo que tiene un solo extremo y se extiende indefinidamente a lo largo de la recta real, en sentido contrario. Las semirrectas pueden ser de cuatro tipos:
Semirrecta derecha y cerrada: 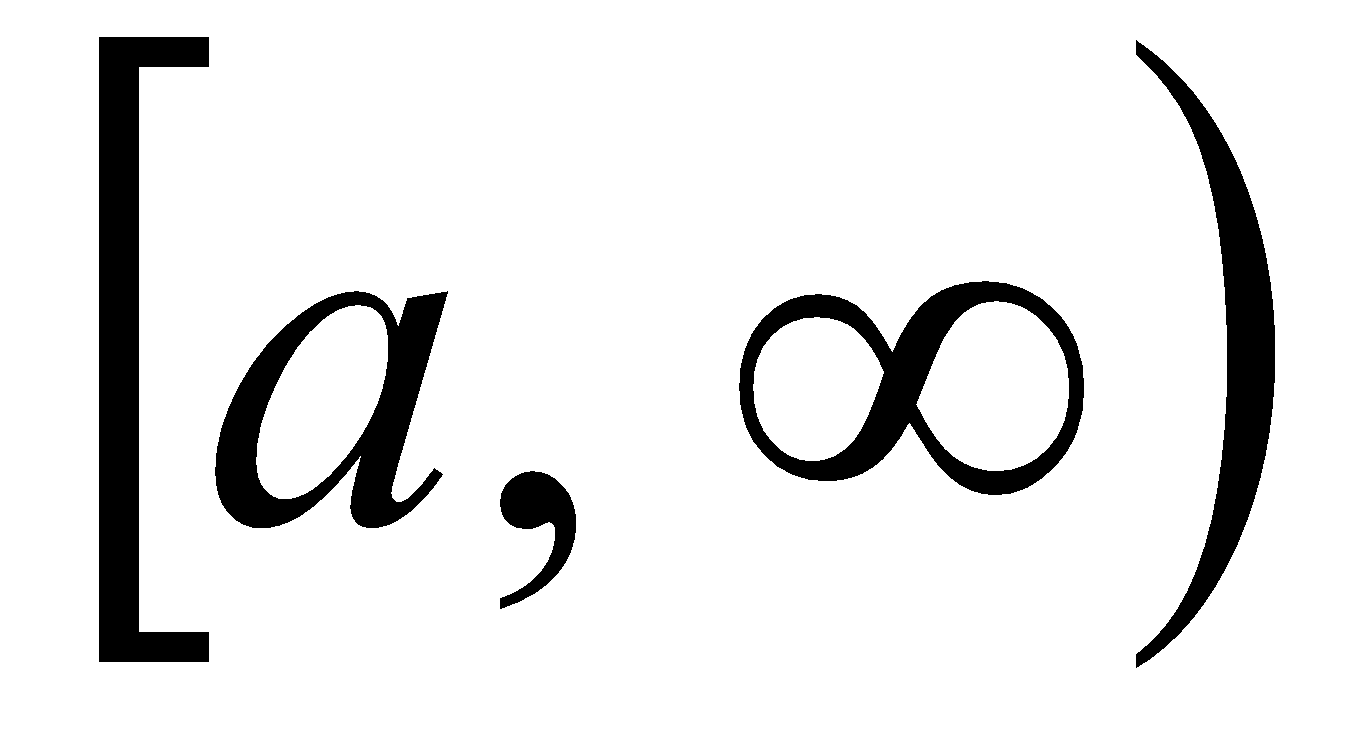
Semirrecta derecha y abierta: 
Semirrecta izquierda y cerrada: 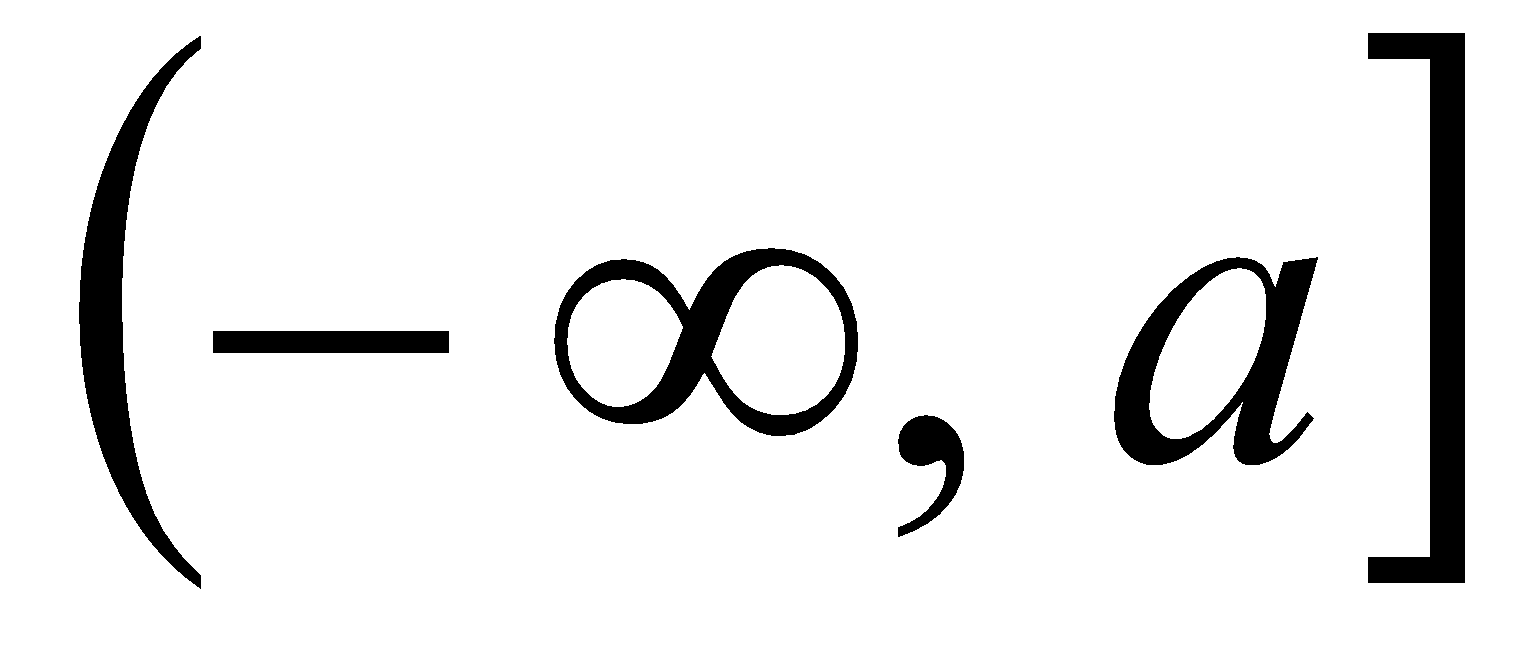
Semirrecta izquierda y abierta: 
Operaciones con intervalos (las más importantes son la unión y la intersección)
- Unión de dos intervalos (a, b) y (c, d) es el conjunto formado por los elementos que pertenecen a uno o a otro intervalo:
(a, b) U (c, d) Ej.: (2, 8) U (6, 10)= (2, 10)
La unión de dos intervalos no es siempre un intervalo:
Ej.: (-3, 5) U (6, 10)
- Intersección de dos intervalos (a, b) y (c, d) es el conjunto formado por los elementos que pertenecen a la vez a uno y otro intervalo:
Ej.: (2, 8)  (6, 10) =
(6, 10) =
La intersección de intervalos es siempre un intervalo.
Cuando los intervalos no tienen elementos comunes su intersección es el conjunto vacío (Ø).
- Clasifica los siguientes números diciendo a qué conjuntos pertenecen (N, Z, Q, R, C):
5; -7; 0.23; 5/4;  ;
; 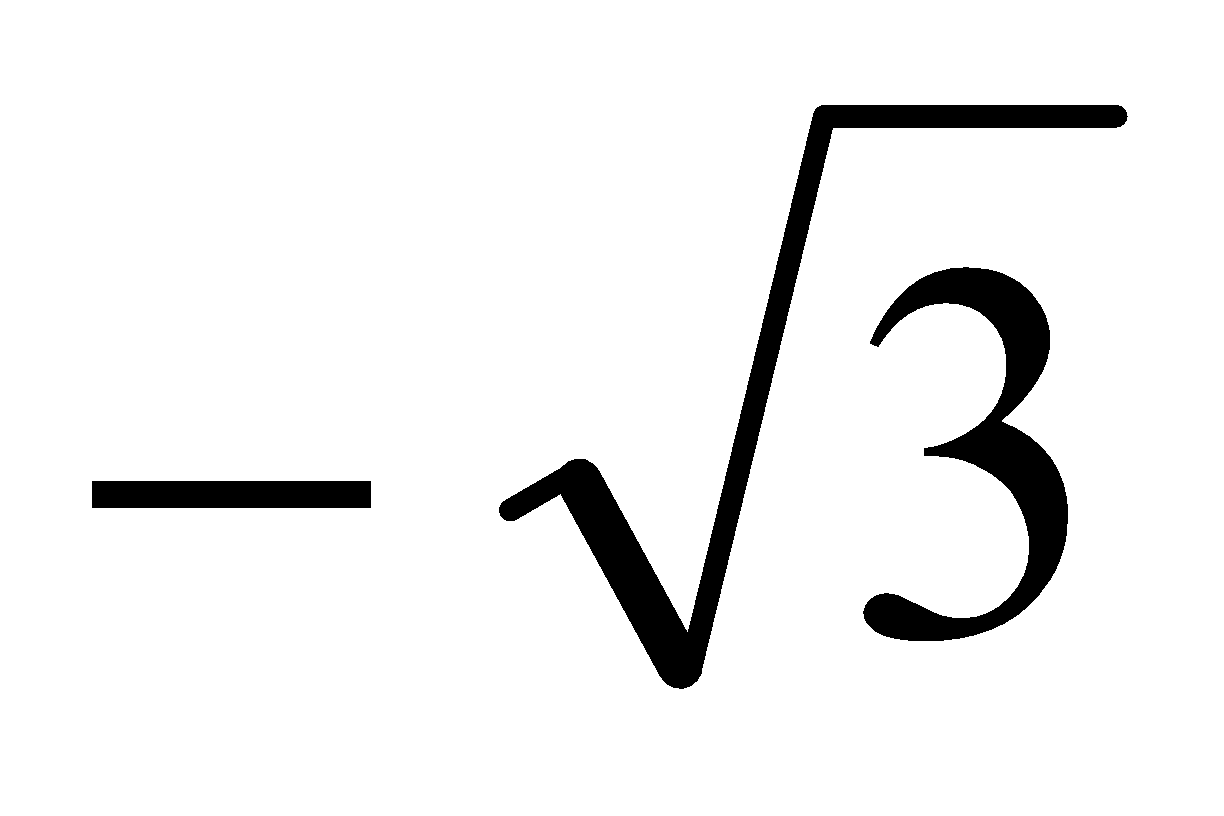 ;
;  ;
;  ;
;  ;
; 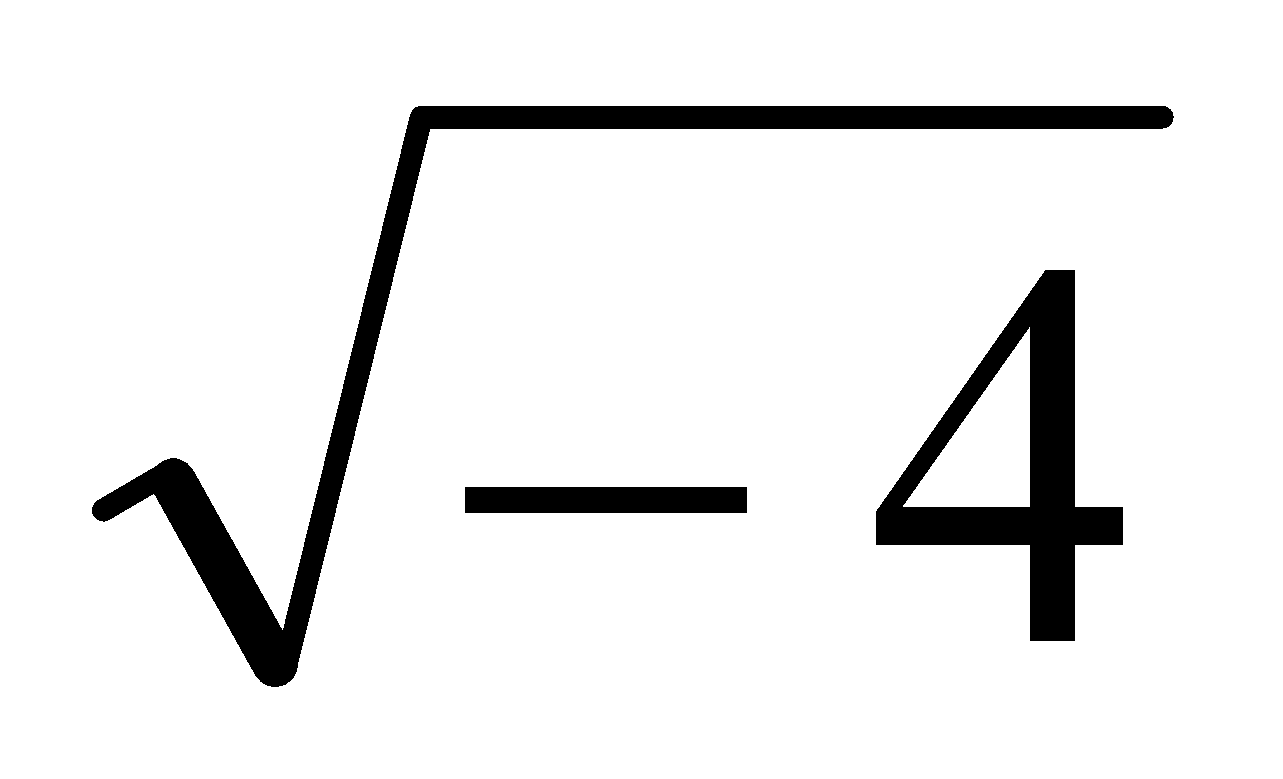 ; -11; -5/10
; -11; -5/10
- ¿Qué números representan D, F y H?
- ¿Cuáles son los números a, b, c, d y e representados en el gráfico?
4. Sobre el segmento  de la recta real, señala el valor numérico de los puntos A y B. Los arcos dibujados tienen por centro 0 y 4 respectivamente y el triángulo pequeño es isósceles.
de la recta real, señala el valor numérico de los puntos A y B. Los arcos dibujados tienen por centro 0 y 4 respectivamente y el triángulo pequeño es isósceles.