EL NÚMERO RACIONAL. CONJUNTO Q. OPERACIONES
Fracción: es un par ordenado de números enteros, de manera que el segundo término del par divide al primero (no siempre de manera exacta). Se puede decir que una fracción es un cociente indicado de dos números enteros, siempre que el segundo (denominador) no sea cero.
Sean a, b 
Z (a, b) = 
es una fracción. Ejemplos: (2, -3) 
= 
= 
;
Z (a, b) = 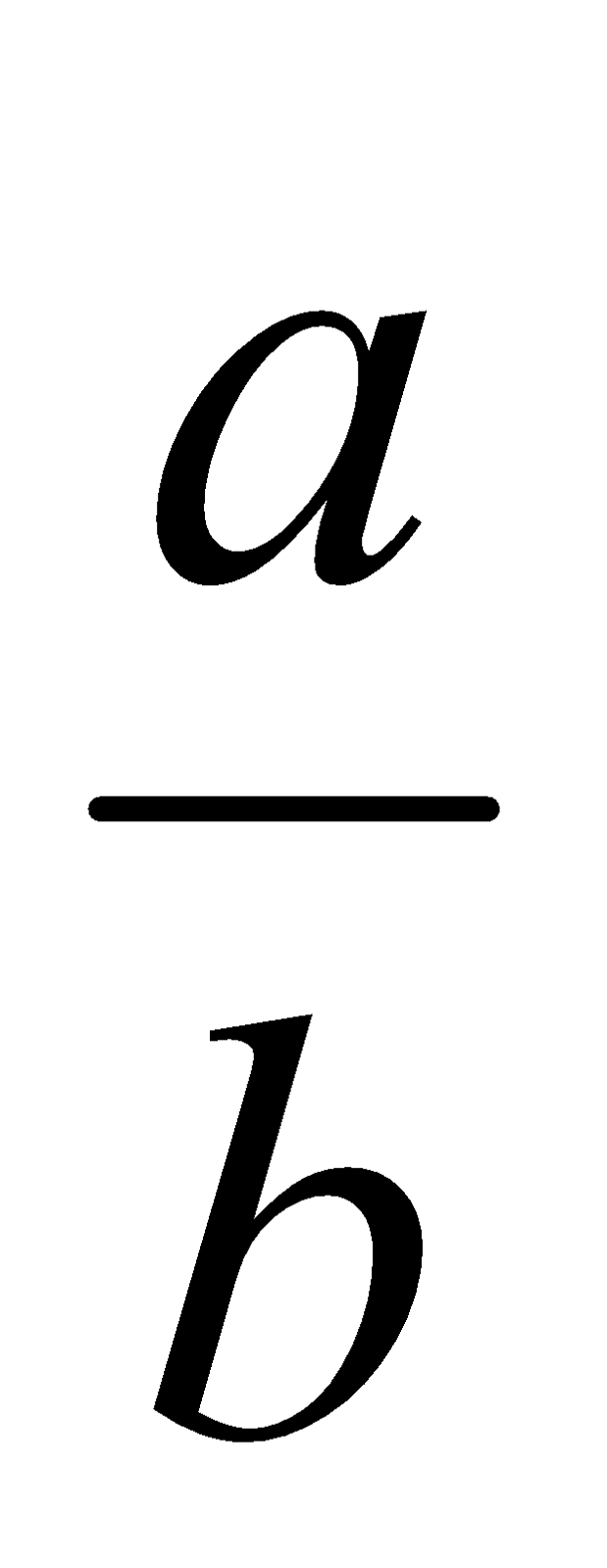es una fracción. Ejemplos: (2, -3) = = ;
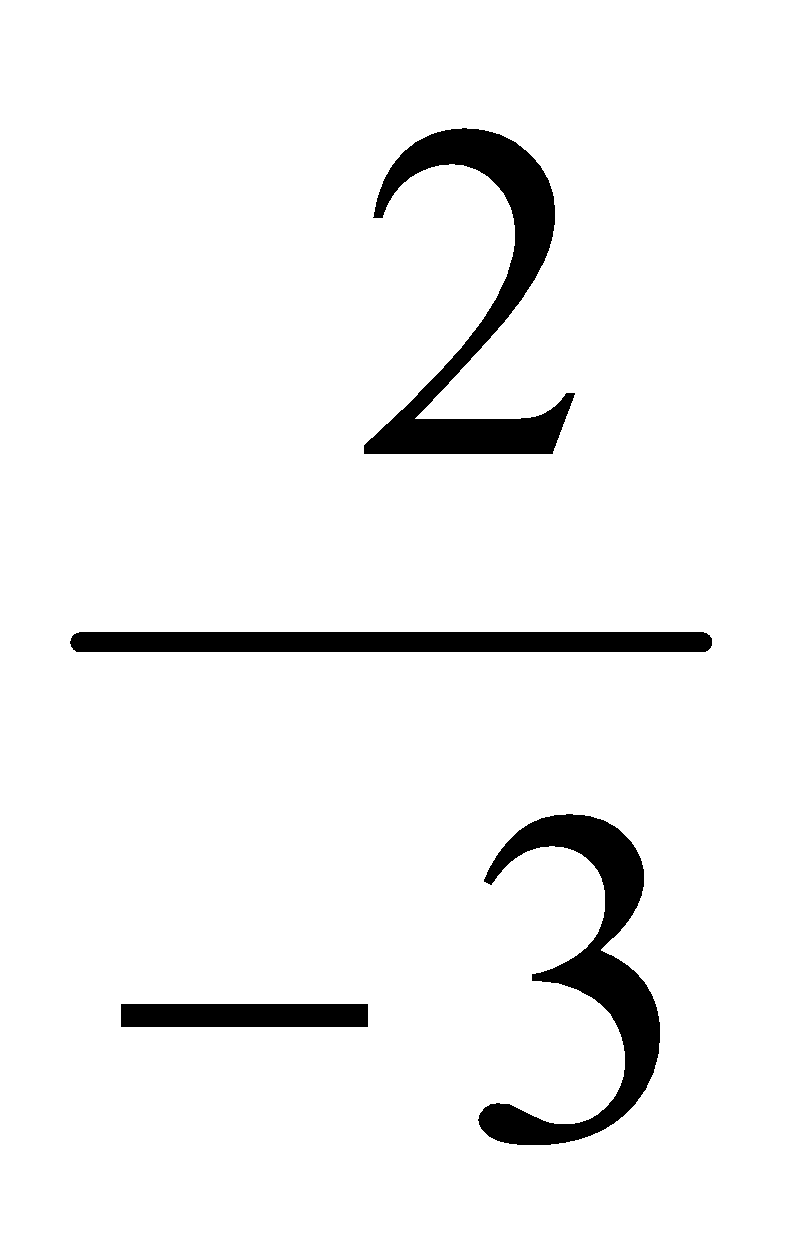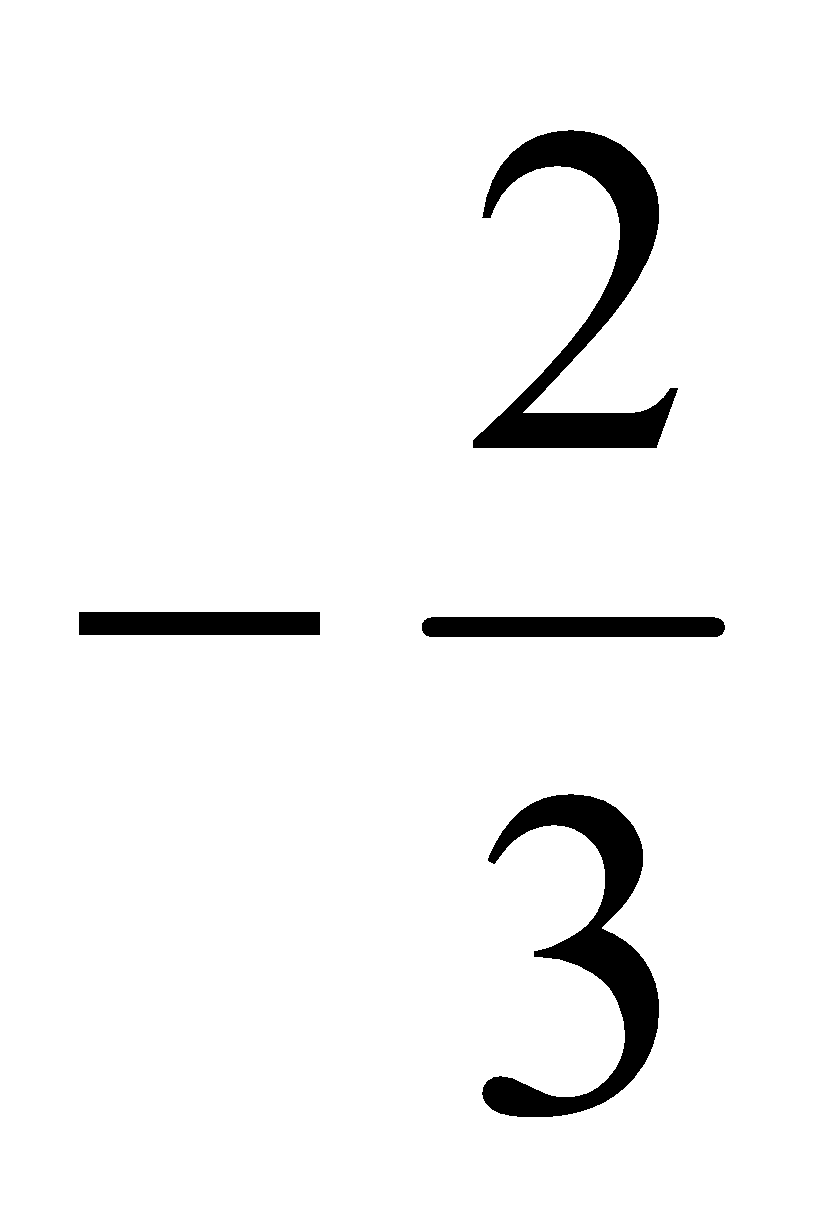(-5, -3) =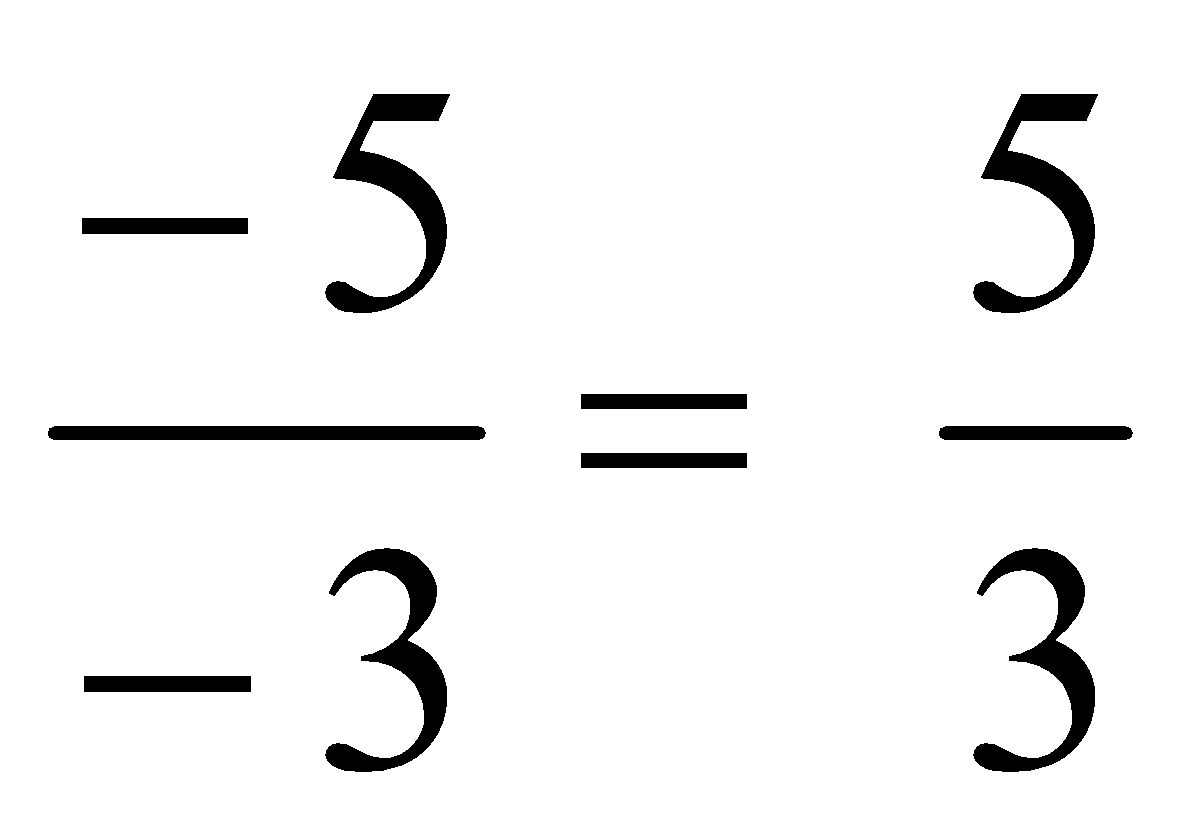 
; (-4, 2) = 
; (-4, 2) =
Nota: No es posible la división por 0.
Equivalencia de fracciones
Una fracción es irreducible cuando el numerador y el denominador son primos entre sí, es decir, cuando ambos tienen de máximo común divisor (M.C.D.). la unidad.
Ejemplos: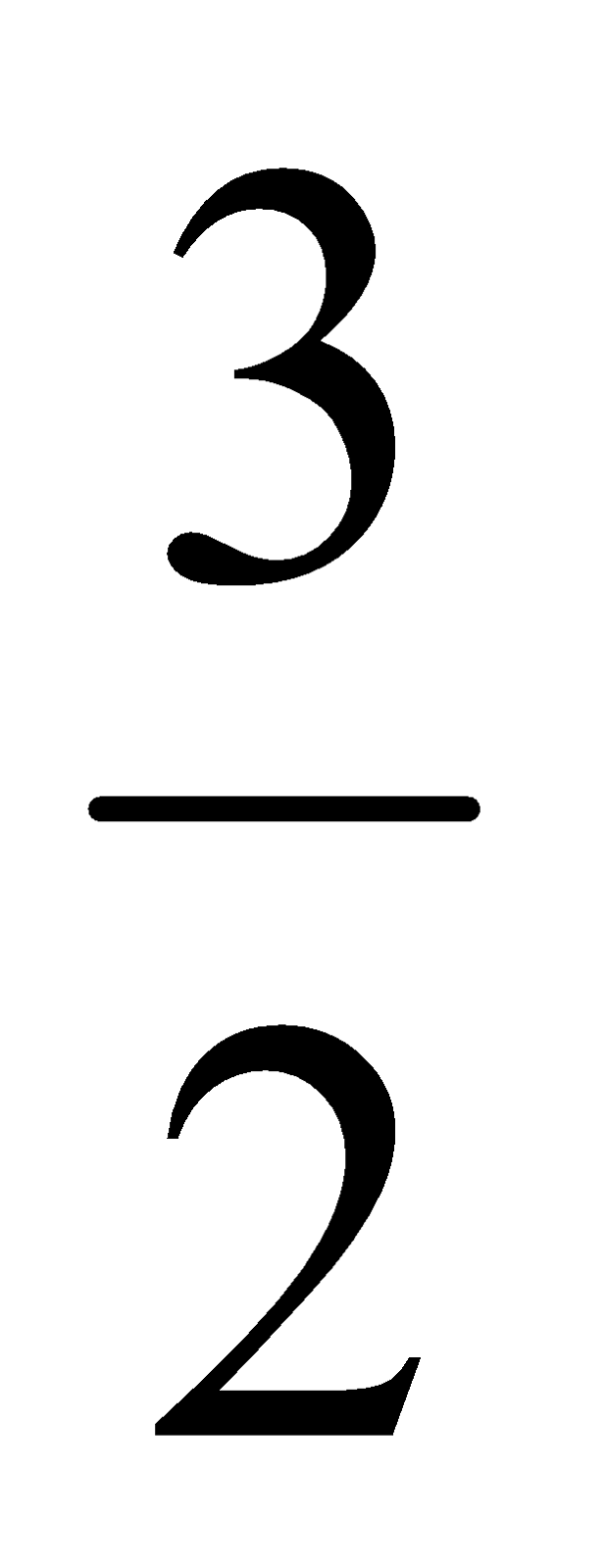 
, 
; 
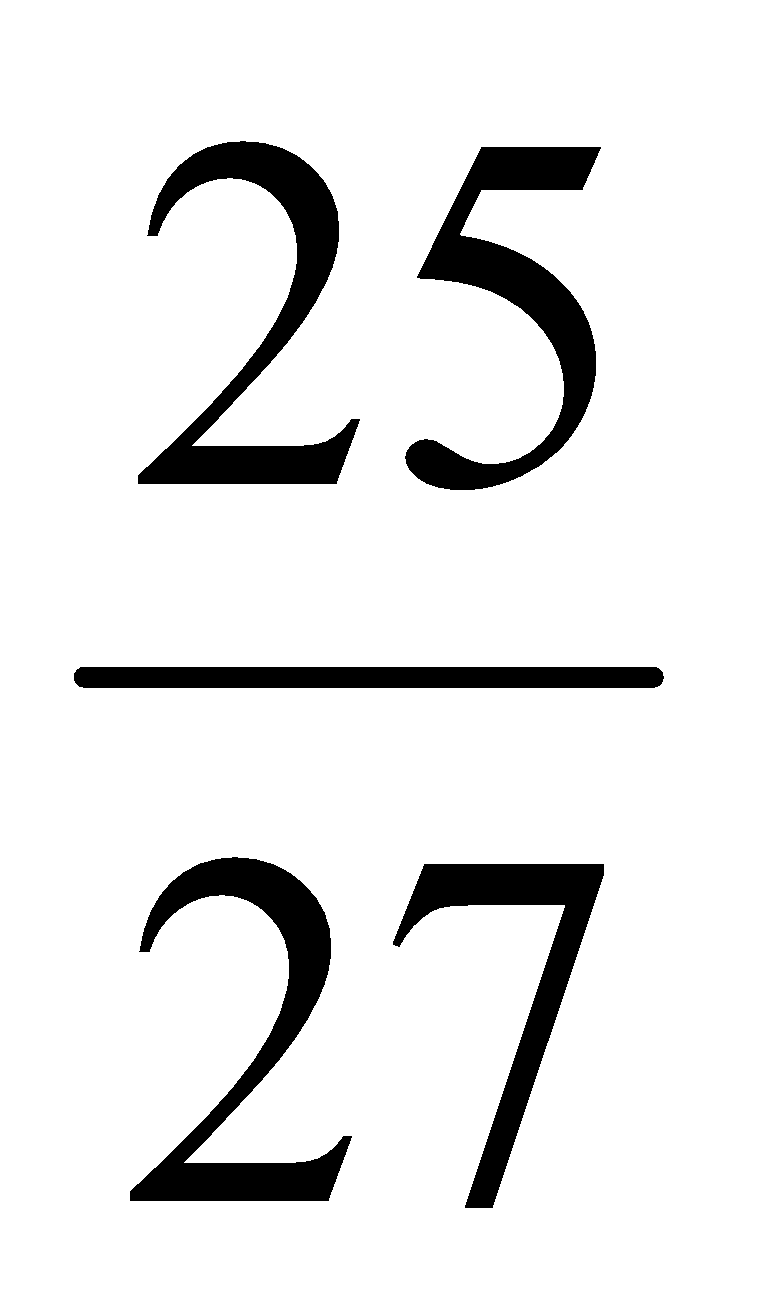son fracciones irreducibles (no se pueden simplificar).
, ; son fracciones irreducibles (no se pueden simplificar).
Una fracción es reducible cuando ambos términos se pueden dividir por un mismo número distinto de 1.
Ejemplos: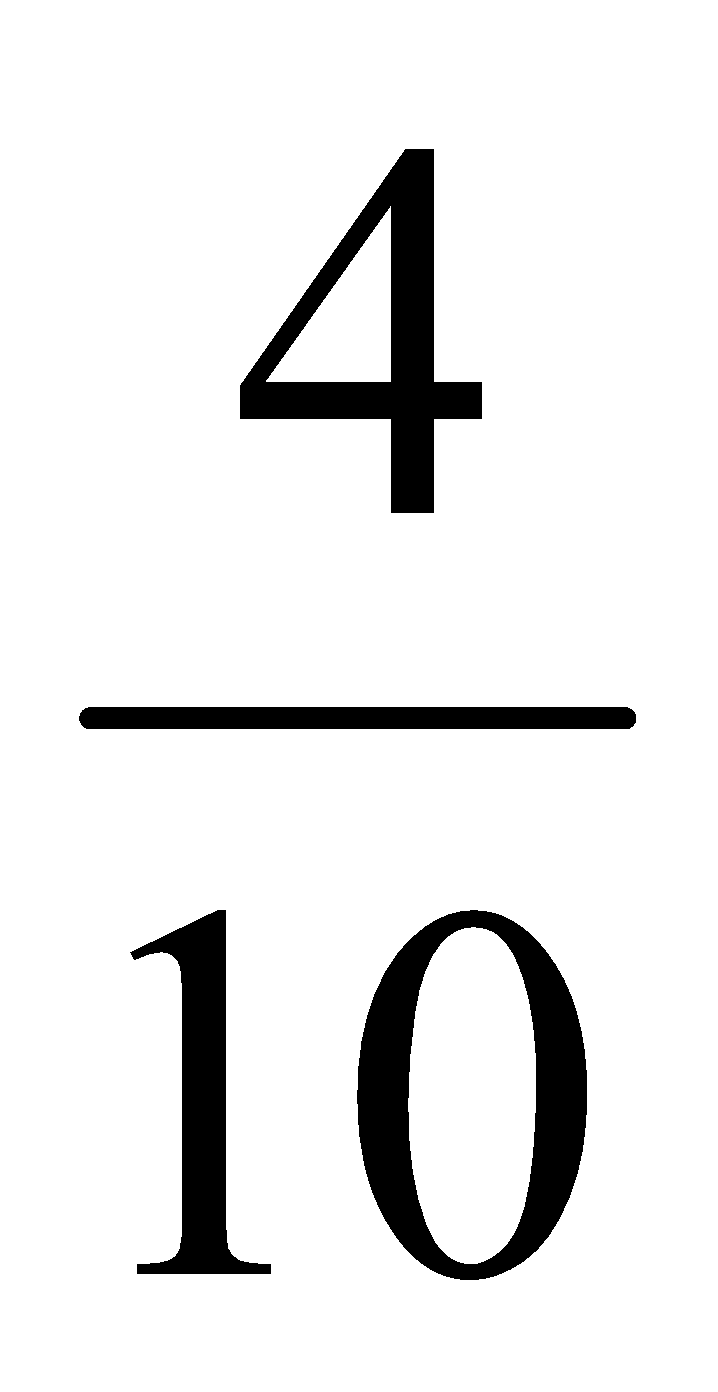 
; 
; 
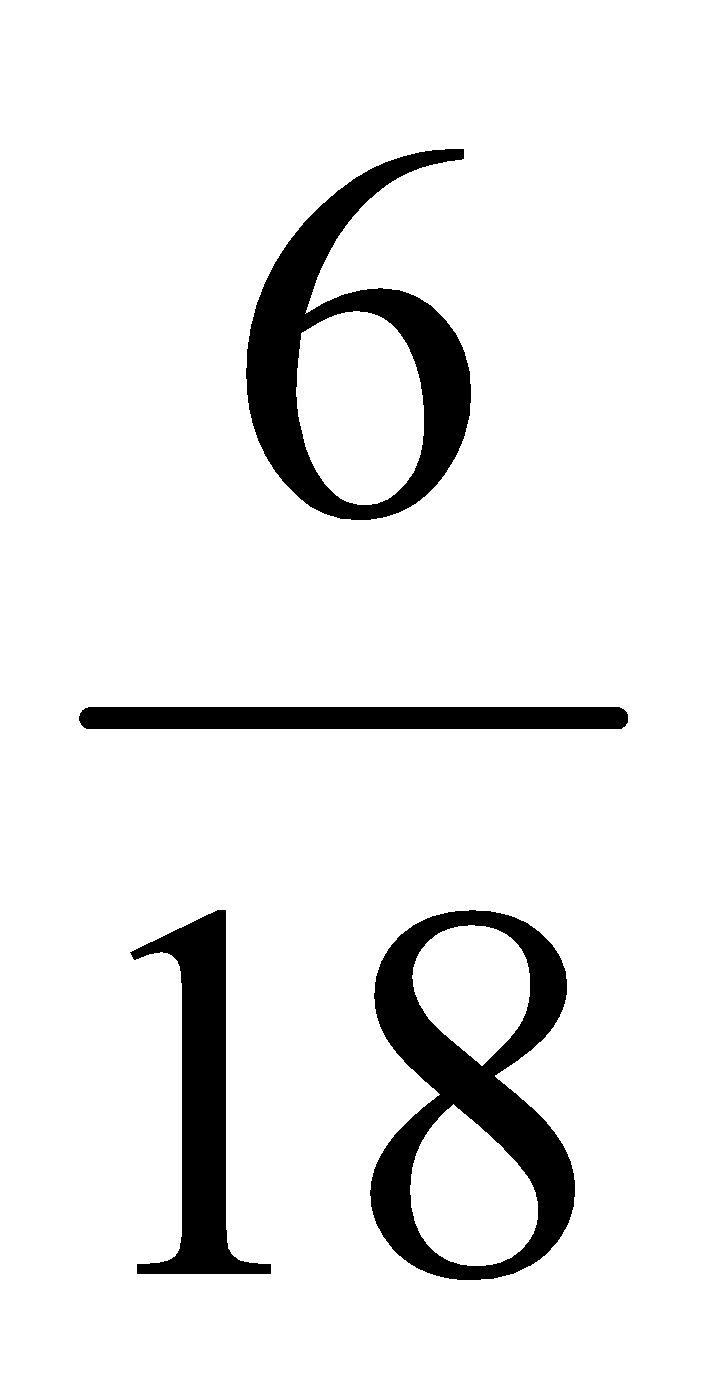son fracciones reducibles (pueden simplificarse hasta su equivalente irreducible).
; ; son fracciones reducibles (pueden simplificarse hasta su equivalente irreducible).
Reducimos una fracción dividiendo ambos términos por un divisor común:
hemos dividido por 2.
Reducimos totalmente una fracción cuando dividimos ambos términos por su M.C.D (producto de los factores COMUNES de ambas cifras elevadas al menor exponente).
M.C.D. (12, 18) = 6 Si dividimos ambos términos por 6: 
siendo 
irreducible.
Ejercicio: Halla las fracciones irreducibles de: ; ;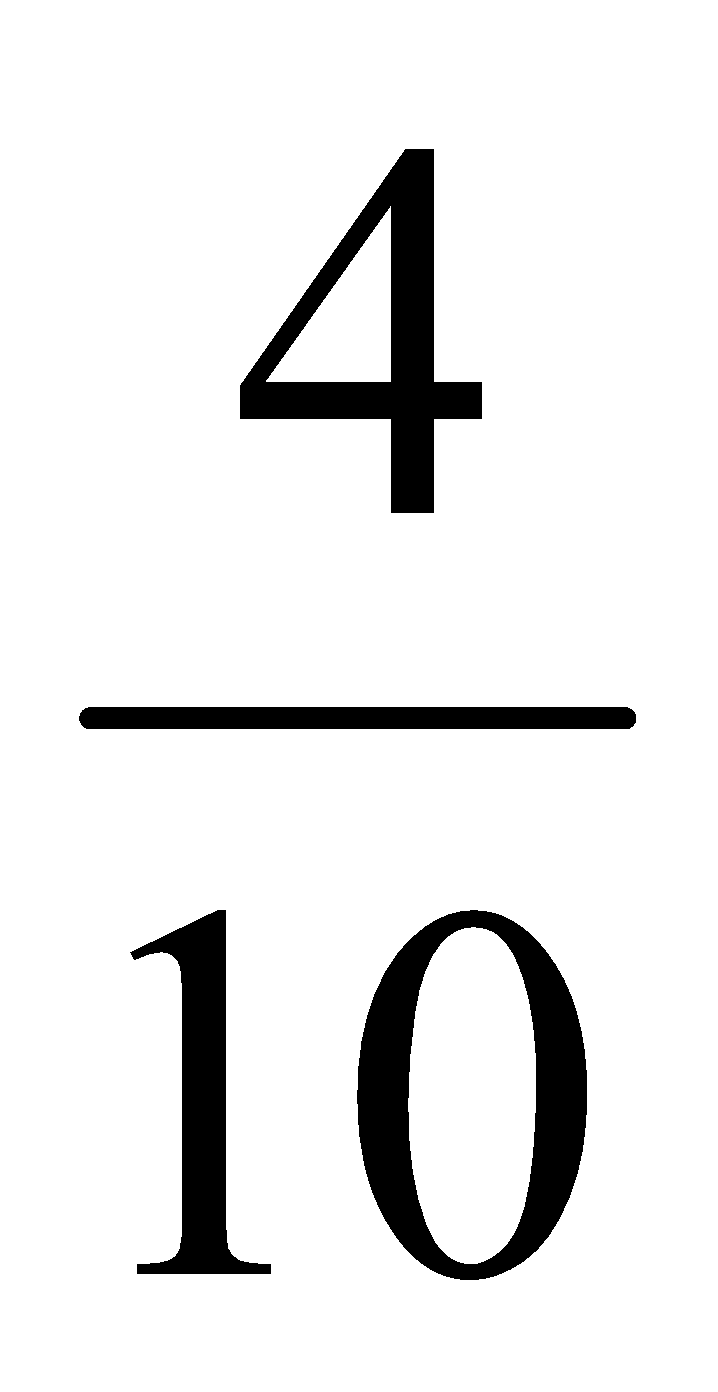
; ;
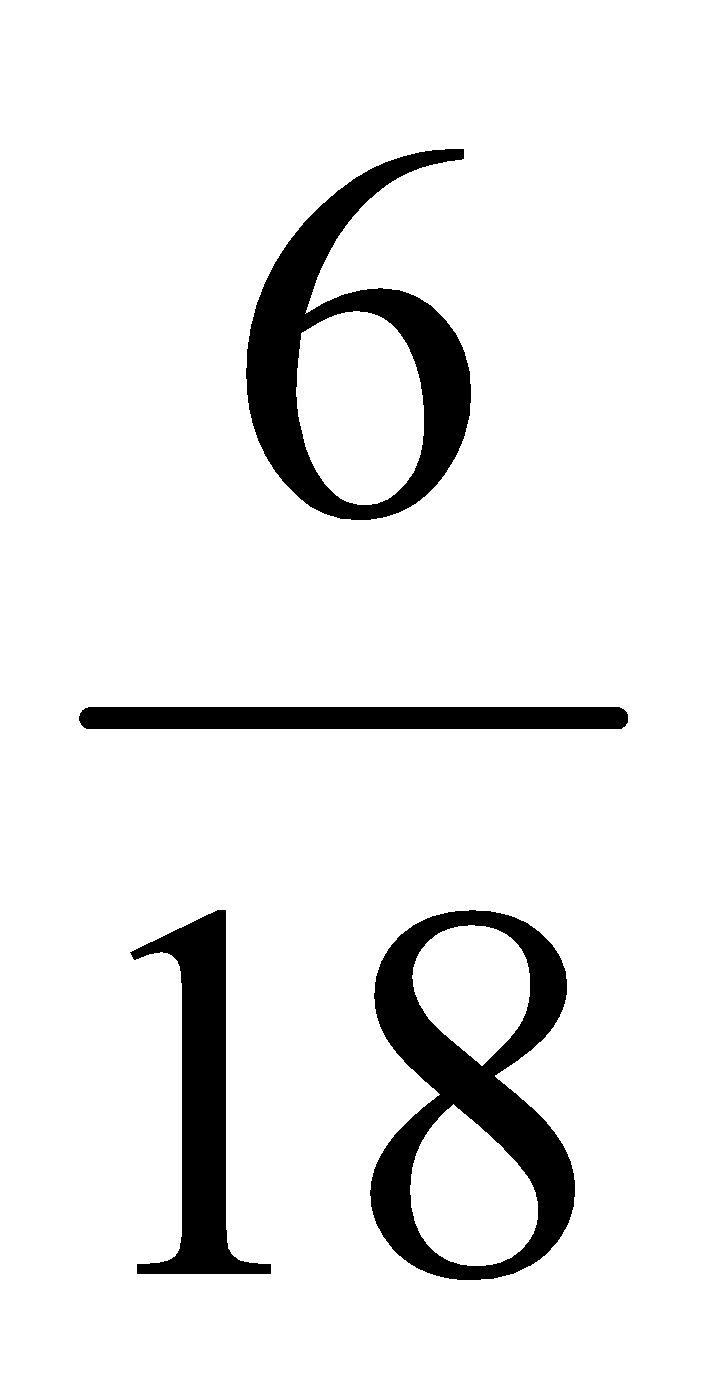Dos fracciones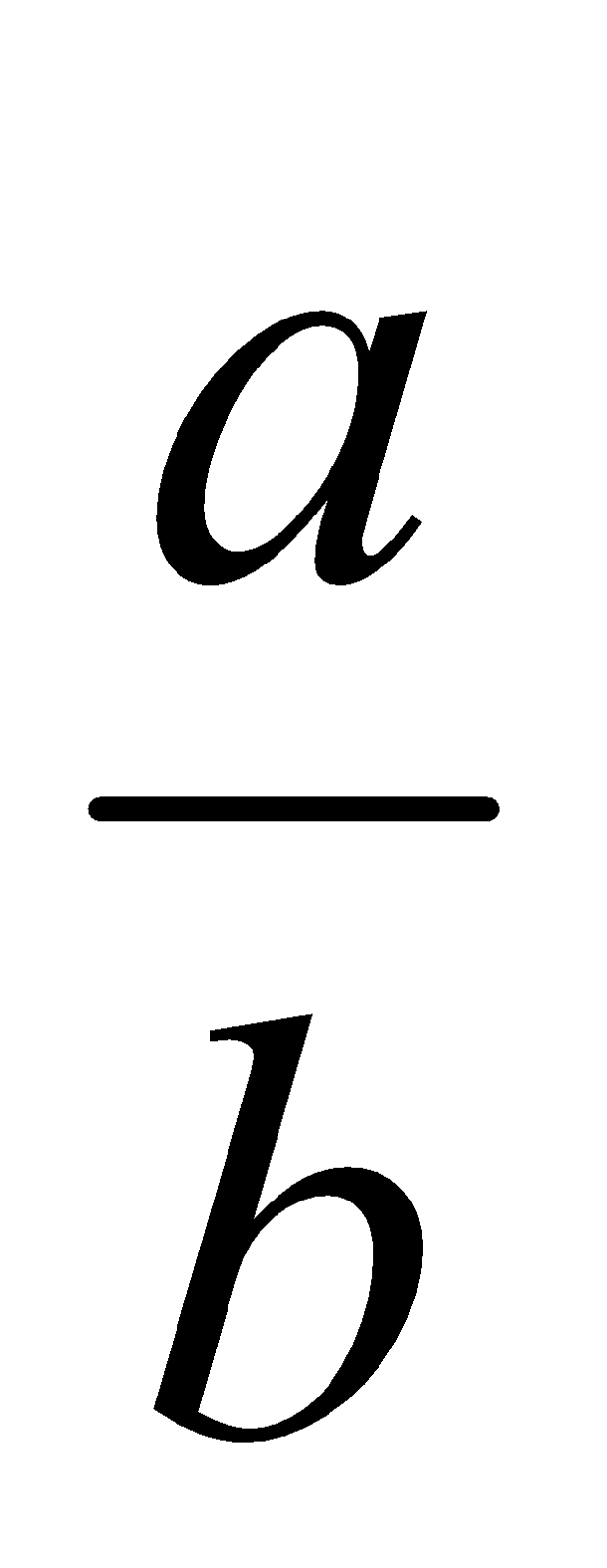 
y 
son fracciones equivalentes si se verifica que a·d = b·c
y 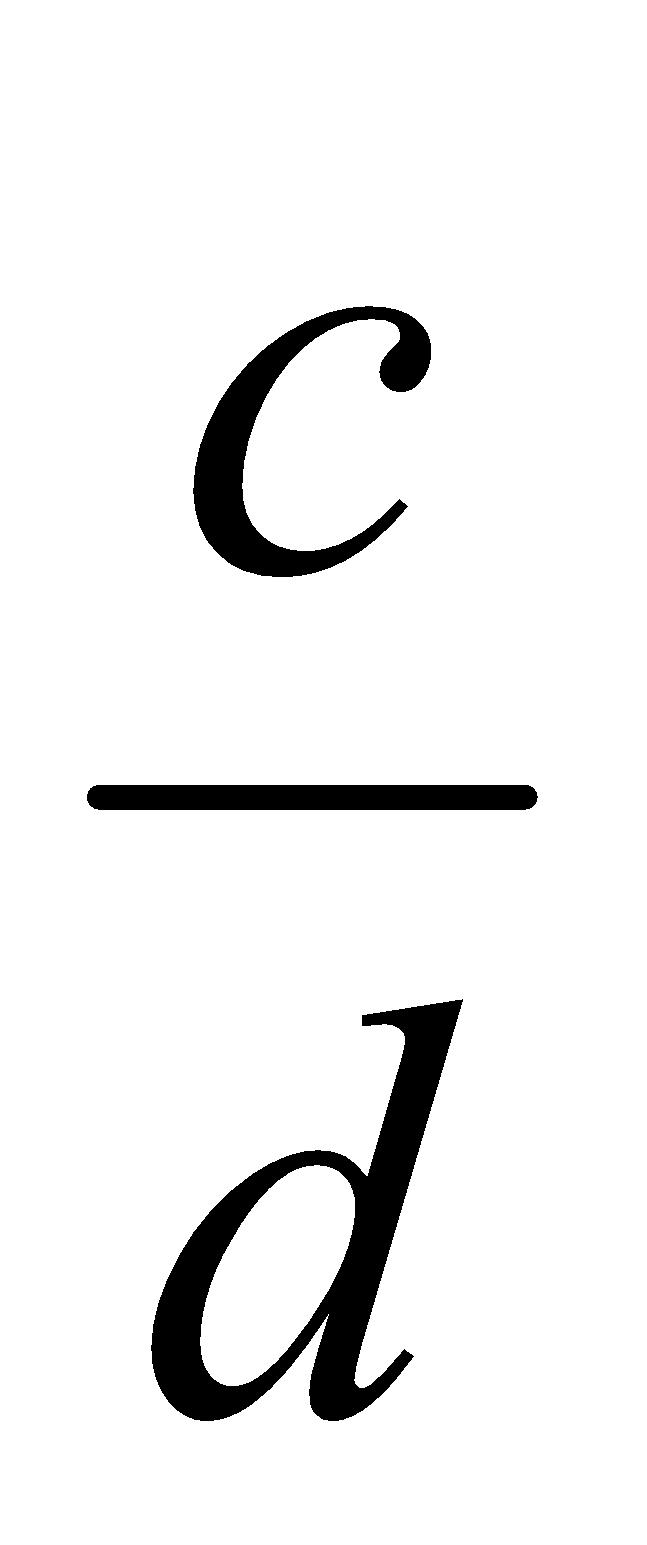son fracciones equivalentes si se verifica que a·d = b·c
Ejemplo: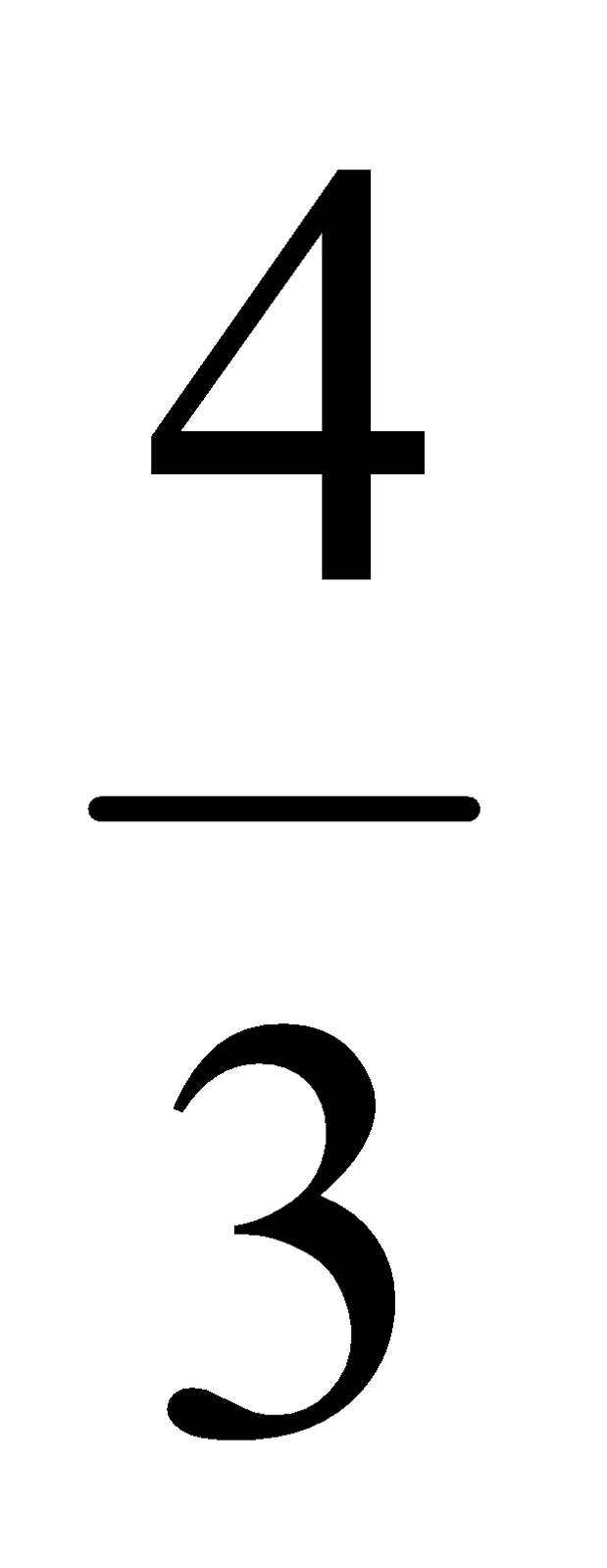 
y 
, ¿son equivalentes? (demuéstralo matemáticamente).
y 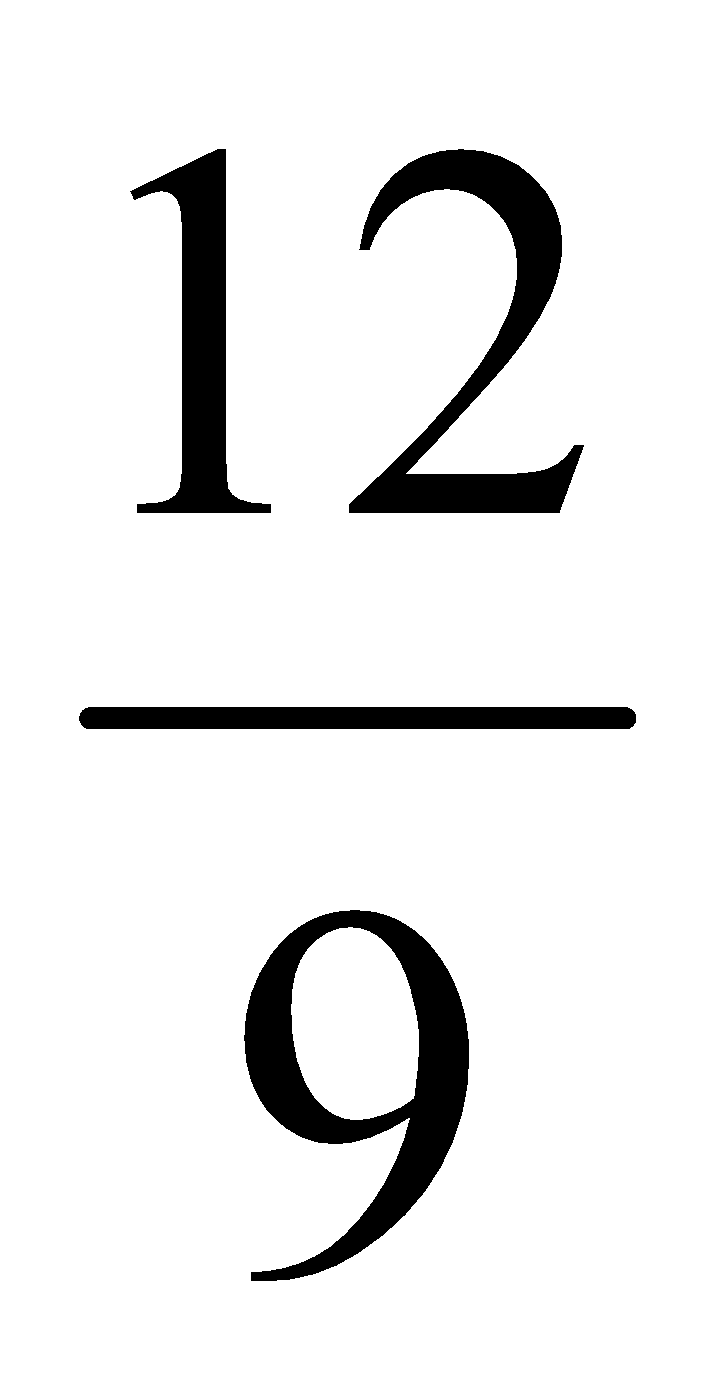, ¿son equivalentes? (demuéstralo matemáticamente).
Dos fracciones equivalentes pueden reducirse totalmente a una misma fracción irreducible.
Ejercicio: Halla las fracciones irreducibles de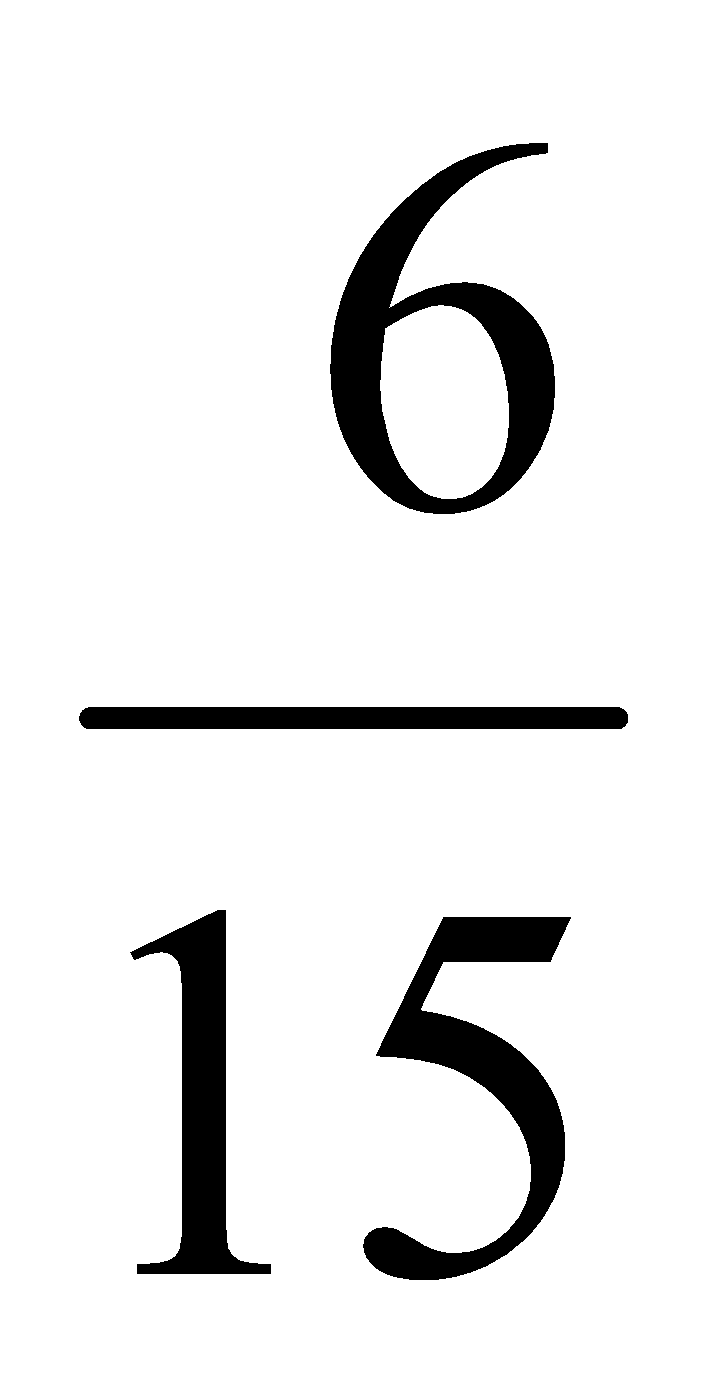 
y 
y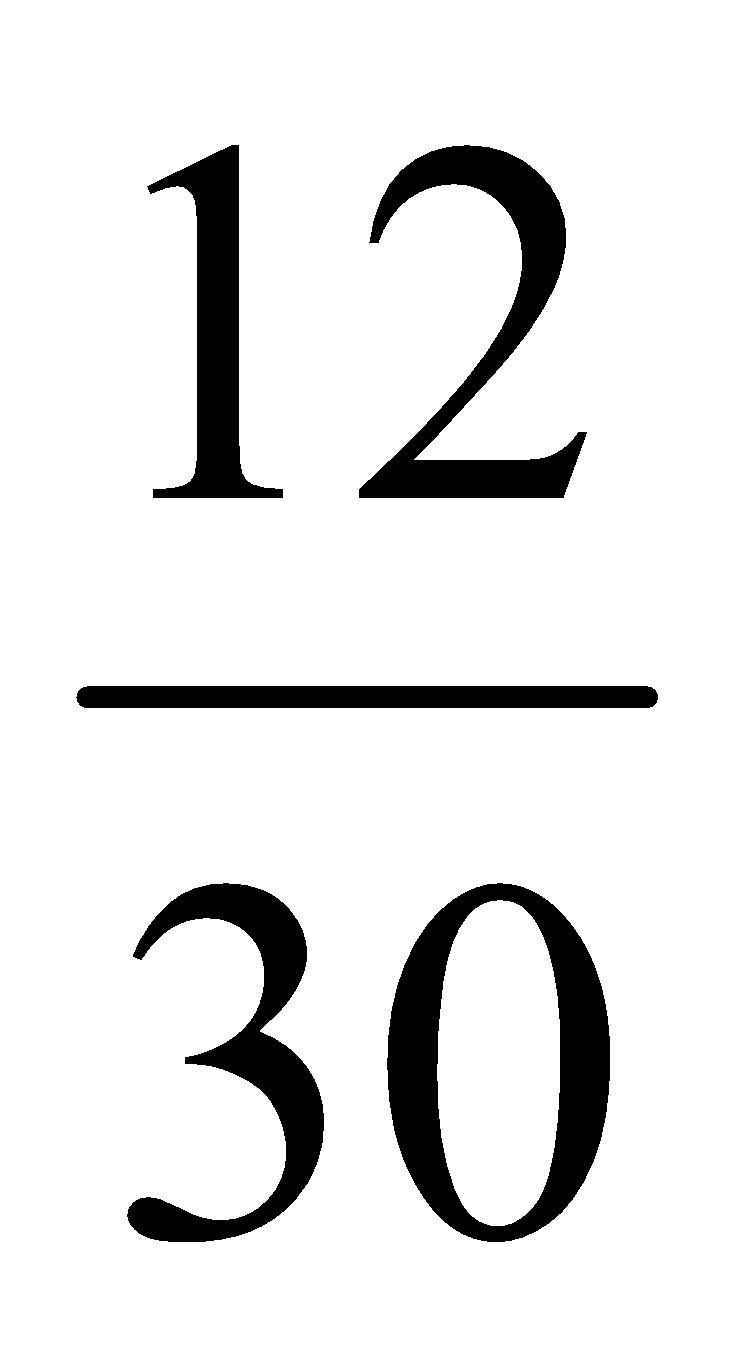
Signo de una fracción
Una fracción es negativa cuando numerador y denominador tienen distinto signo:
; 
Una fracción es positiva cuando numerador y denominador tienen el mismo signo:
; 
NÚMERO RACIONAL. CONJUNTO Q
Todaas las fracciones equivalentes entre sí representan un solo número racional. Así, puede decirse que un número racional es una fracción y todas sus equivalentes.
Ejemplo: 
Todas estas fracciones representan al mismo número racional:
. Demuéstralo.
Todas estas fracciones representan al mismo número racional:. Demuéstralo.
Clases de numeros racionales:
- Números racionales enteros
Son los números racionales en los que el denominador divide al numerador de manera exacta.
Ejemplos: 
; 
(Todos los números enteros son racionales ya que podemos expresarlo como fracción de dos números)
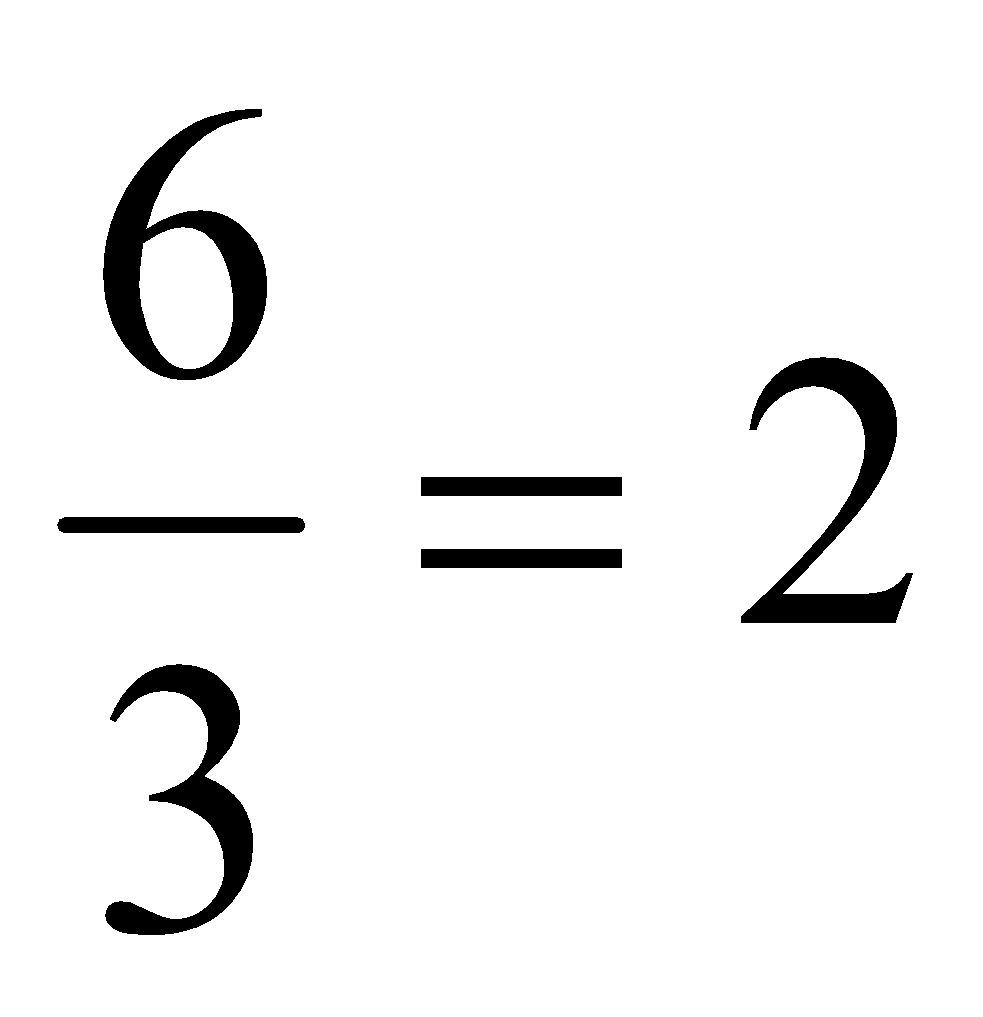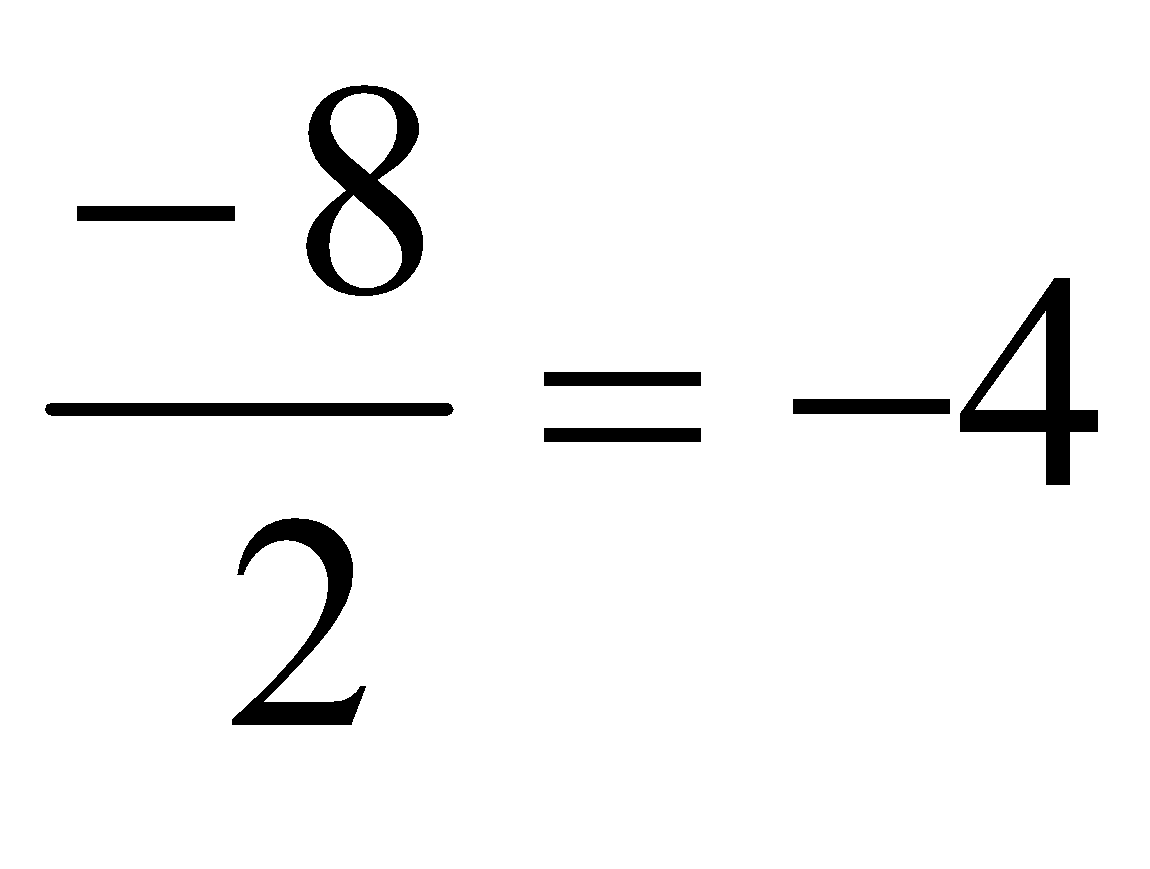; (Todos los números enteros son racionales ya que podemos expresarlo como fracción de dos números)- Números fraccionarios
Son los números racionales en los que el denominador no divide de manera exacta al numerador.
Ejemplos: 
; 
;
Operaciones con números racionales
Suma de números racionales:
- Si tienen el mismo denominador: se suman los numeradores y se deja el mismo denominador.
Ejemplo:
Ejercicio: 
b) Si tienen distintos denominadores: se reducen a común denominador que será el mínimo común múltiplo (m.c.m: producto de factores comunes y no comunes al máximo exponente), se pone el denominador obtenido y se suman los nuevos numeradores (obtenidos multiplicando cada numerador por el m.c.m. y dividiendo cada producto por su anterior denominador).
Ejercicio: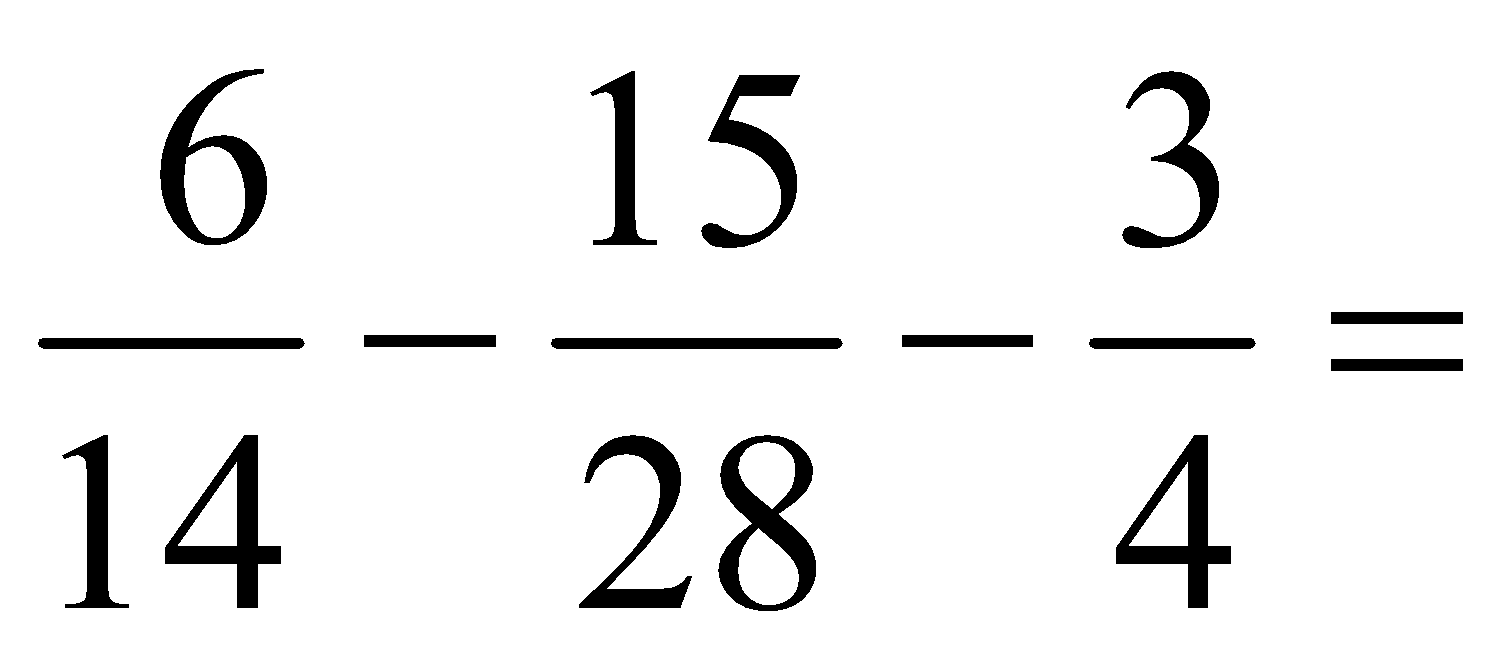 
=
Las propiedades de la suma de los números racionales son las mismas que las de la suma de los números enteros (asociativa, conmutativa, elemento neutro y elemento opuesto) y además:
Es uniforme: La suma de dos o más números racionales tiene un resultado único, independientemente de las fracciones (equivalentes) que representen a cada número.
Si utilizamos los siguientes equivalentes de las anteriores fracciones:
Producto de números racionales:
El producto de dos o más fracciones es igual al producto de los numeradores partido por el producto de los denominadores: 
(Multiplicamos en línea)
(Multiplicamos en línea)
Ejercicios: 
Las propiedades de la multiplicación de los números racionales son las mismas que las de la multiplicación de los números naturales y/o enteros (asociativa, conmutativa, elemento neutro y distributiva respecto de la suma) y además:
a) Es uniforme: El producto de dos o más números racionales tiene un resultado único, independientemente de las fracciones (equivalentes) que representen a cada número.
Ejercicio: 
b) Inverso: El inverso de un número racional es otro número racional que multiplicado por el primero da como resultado 1: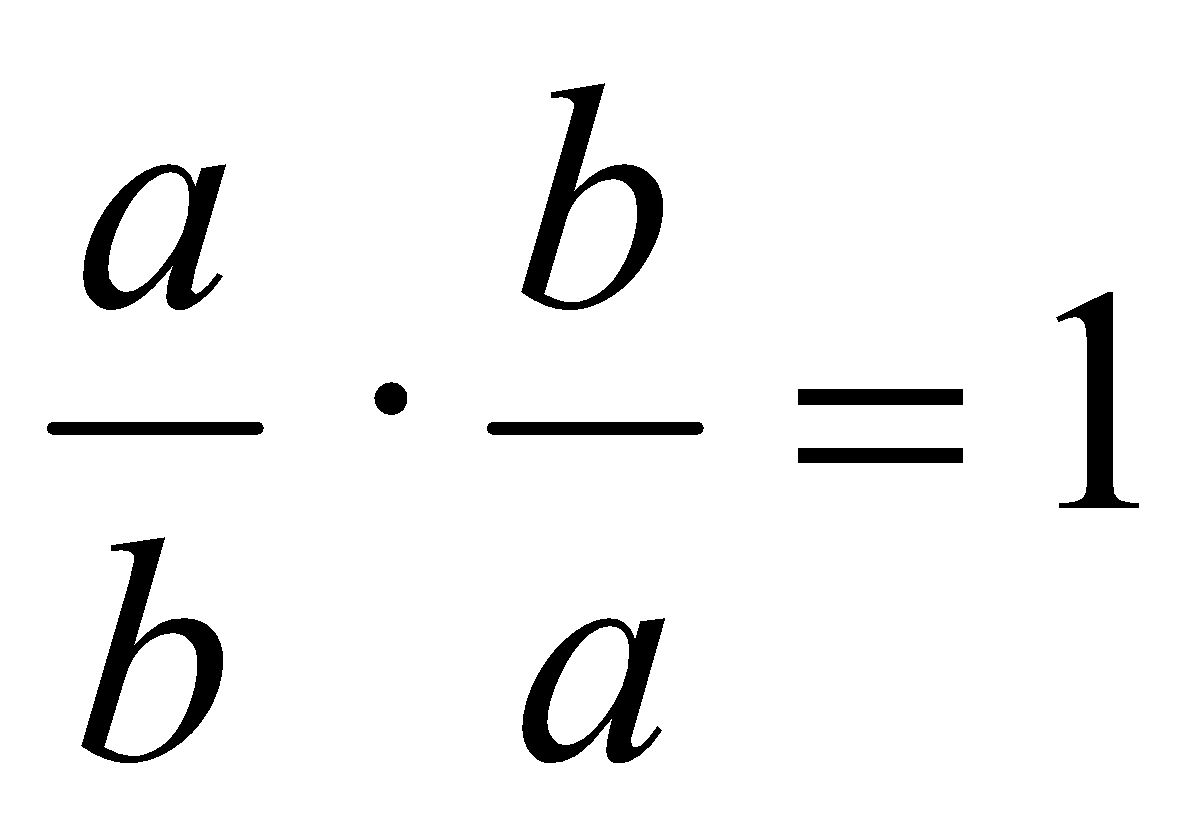 
Al inverso también se le llama recíproco.
Al inverso también se le llama recíproco.
Ejercicios ¿Cuál es el inverso de 
?
?
Halla los inversos de:
; 
; 
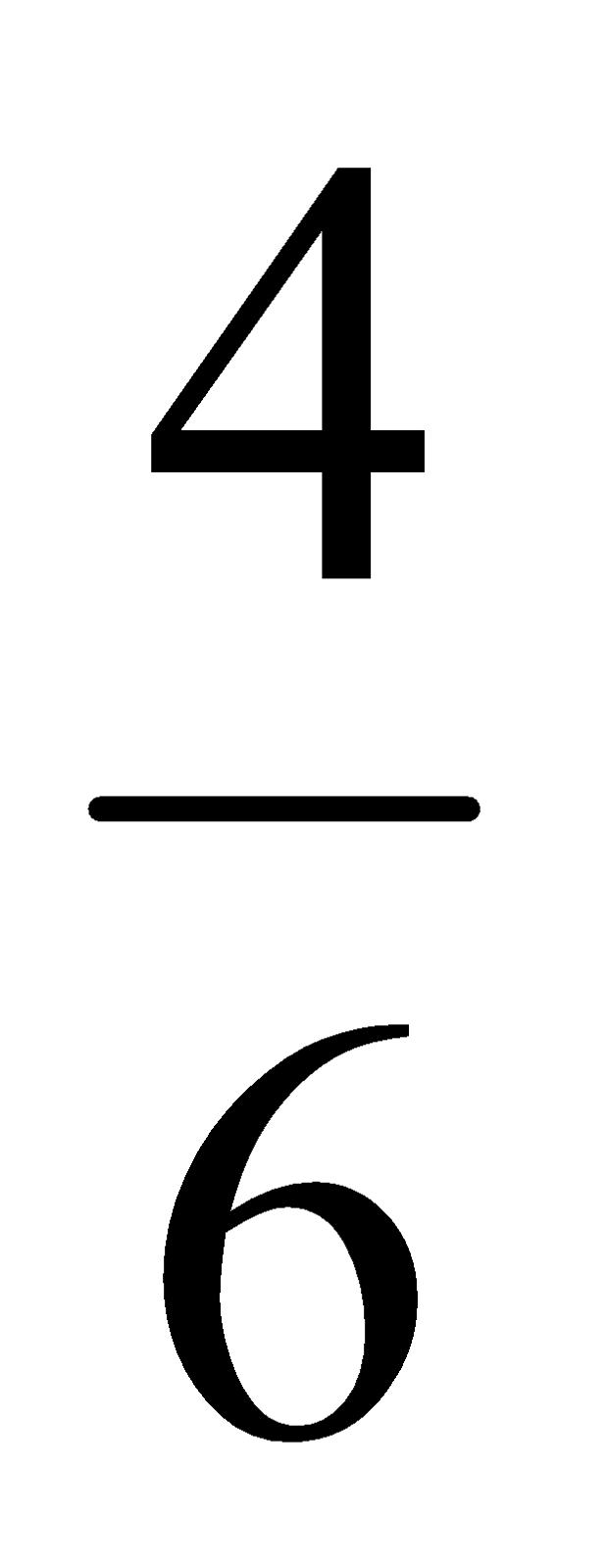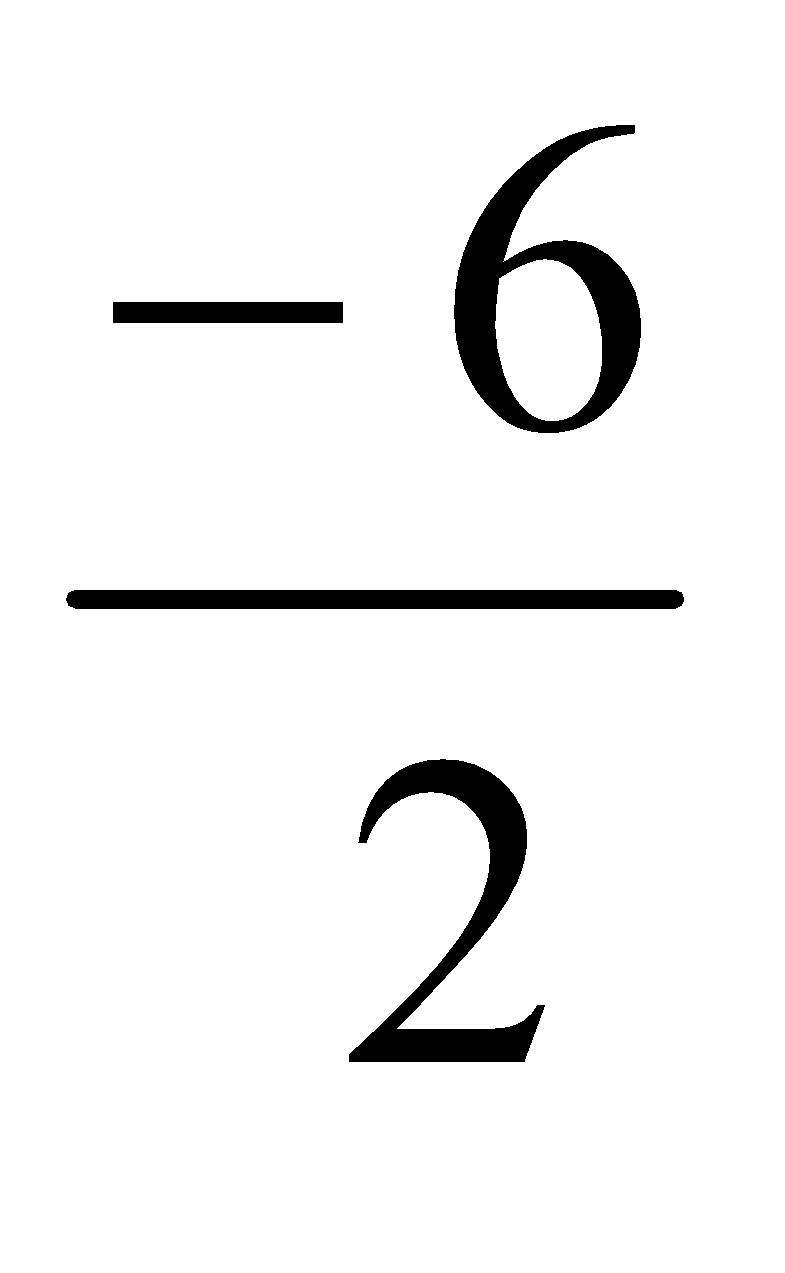; -3
; ; ; -3
Nota: el producto de un número racional por 0 es igual a 0. 
Ejemplo: 
División de dos números racionales:
Para dividir dos números racionales multiplicamos el numerador del primer racional por el divisor del segundo racional y viceversa. (Multiplicamos en x, en aspa)
Ejemplo: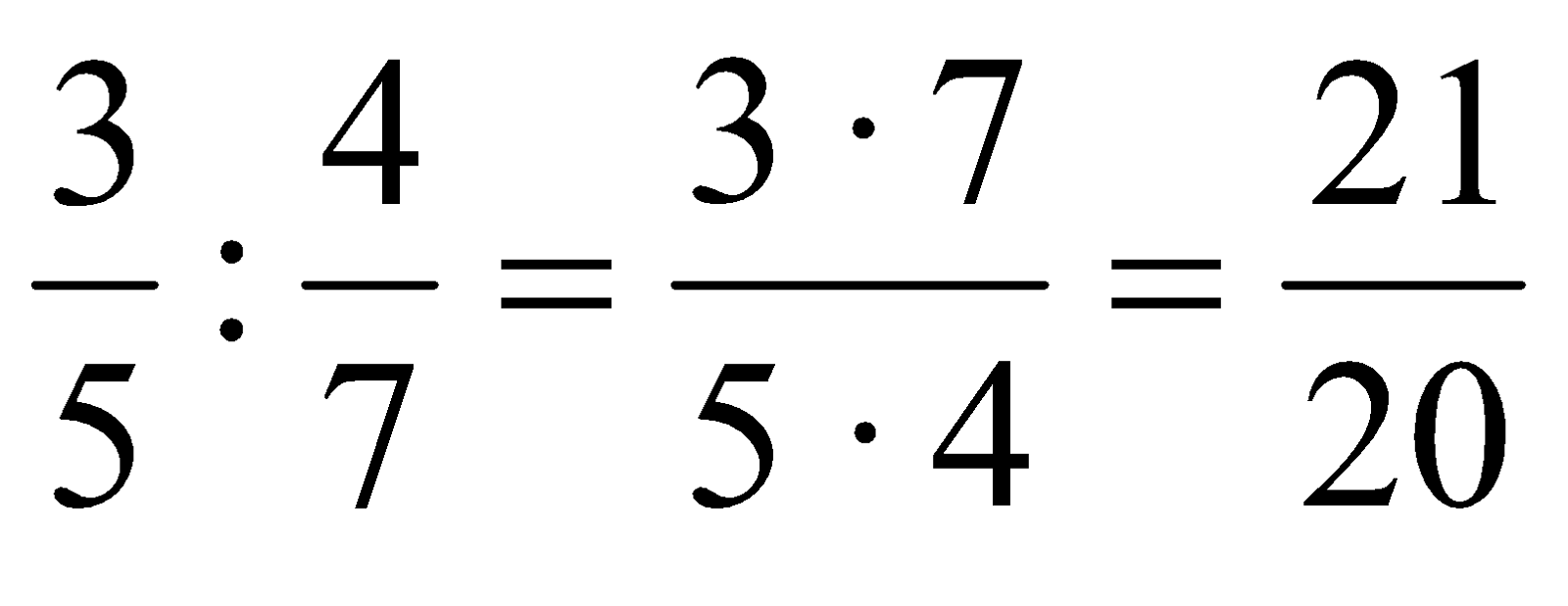 
Ejercicios: 
Nota: La división por 0 nunca es posible.
NÚMEROS DECIMALES
Un número decimal es el que se representa por un número entero seguido de una coma y una o varias cifras decimales. Ejemplos: 12, 384; -4,28
- Decimales finitos: Tienen un número finito de cifras decimales. Ej.: 6,54
Podemos expresarlos como fracción colocando en el numerador el número sin la coma, y en el denominador, la unidad seguida de tantos ceros como cifras decimales haya:
6,43 =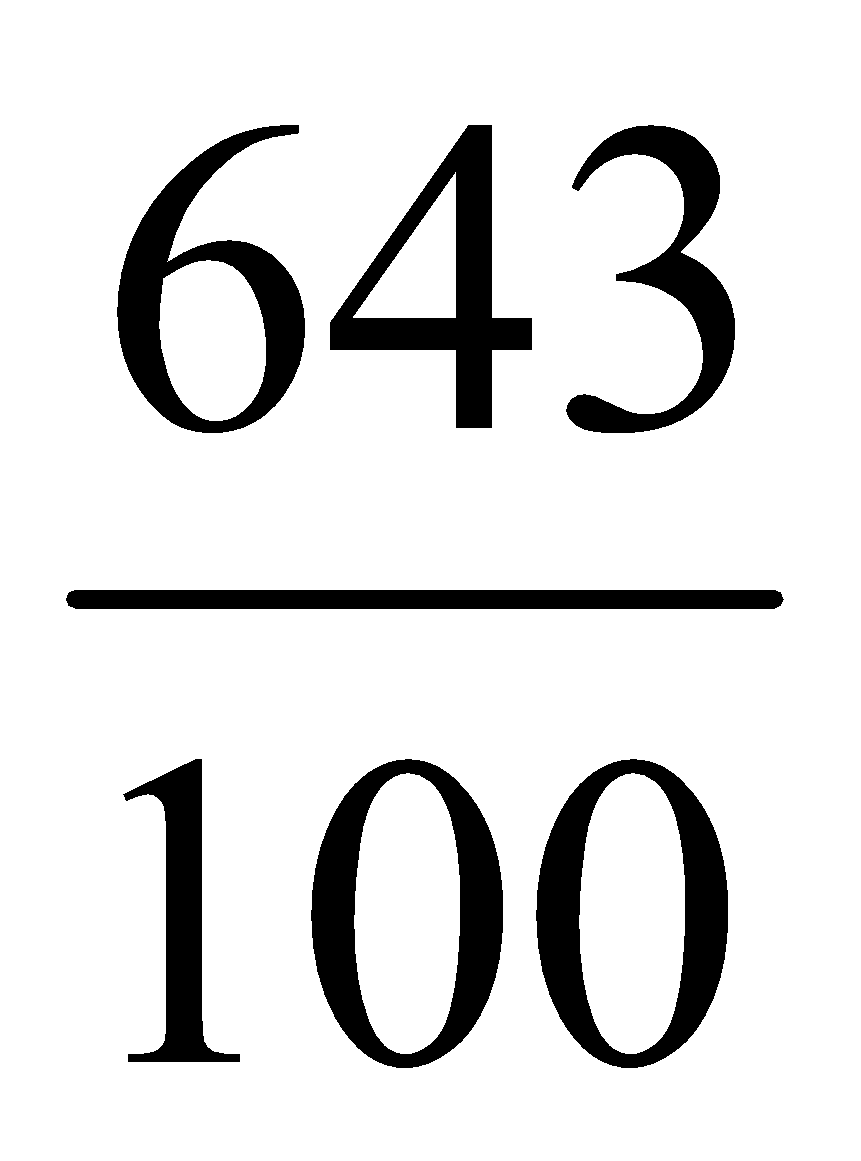 
; 8,163 = 
; 47,213 = 
; 8,163 = ; 47,213 =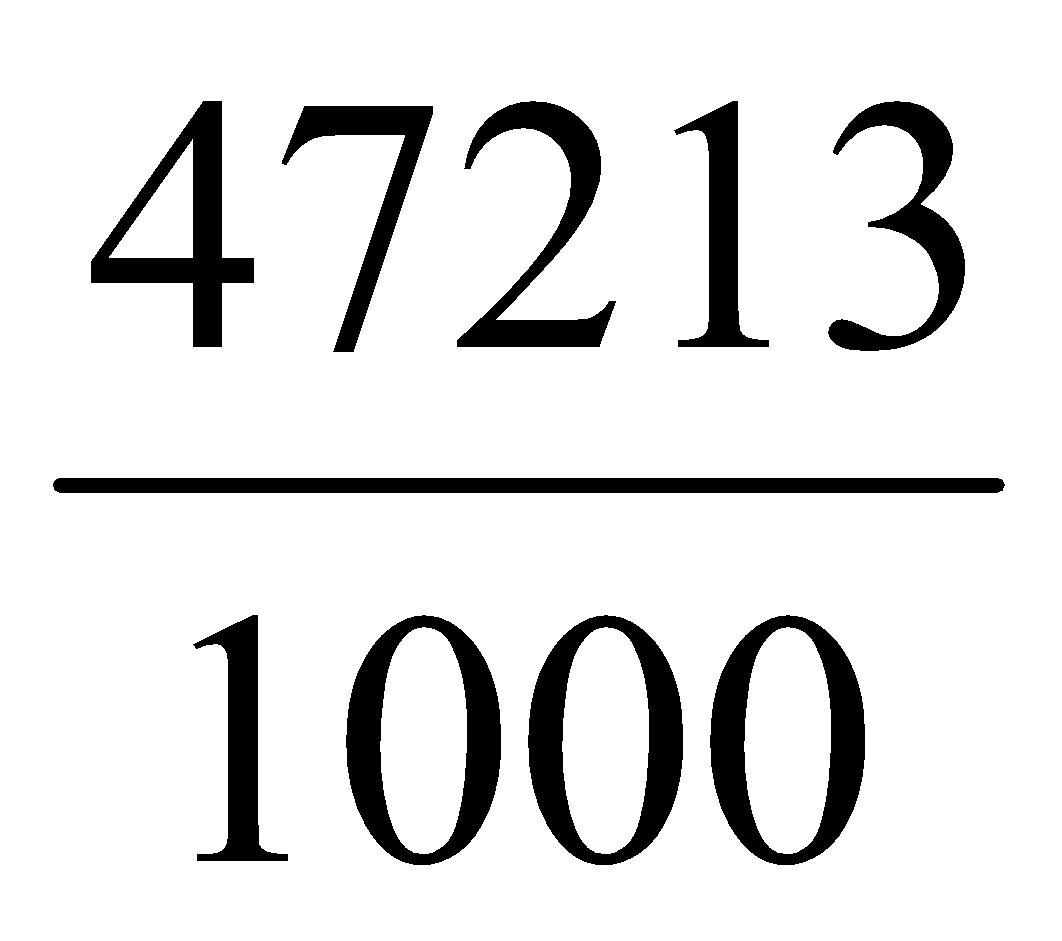
Los números decimales finitos pertenecen a Q (números racionales).
- Decimales infinitos: Tienen un número infinito de decimales. Pueden ser de dos tipos: periódicos y no periódicos.
b1) Periódicos: Un número decimal periódico es aquel que, teniendo infinitas cifras decimales, hay una cifra o un grupo de cifras que se repiten indefinidamente:
4,6666…; 72,38383838…; 15.29575757…
Se expresan colocando un arco sobre la cifra o grupo de cifras que se repiten, así:
4,6666… =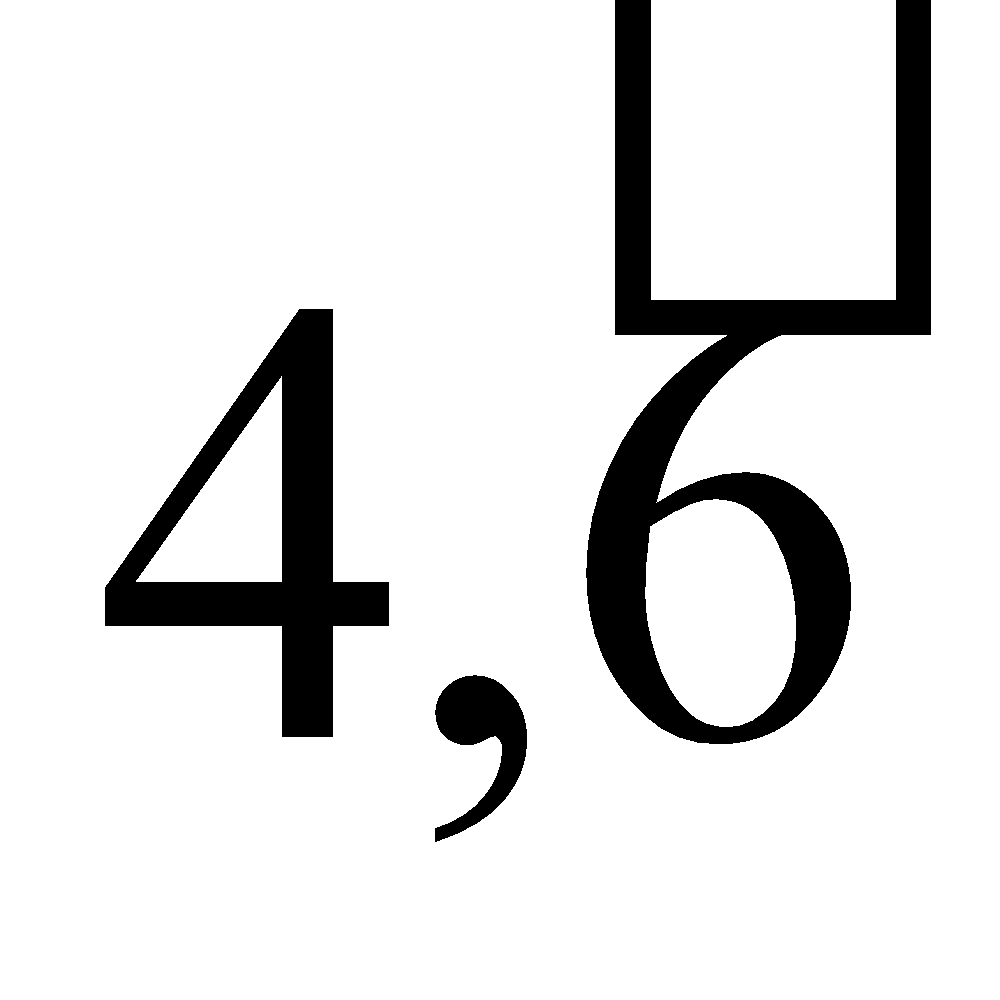 
; 72,383838… = ; 15.295757 57… =
; 72,383838… = ; 15.295757 57… =
La cifra o grupo de cifras que se repiten se llama periodo.
Los números decimales periódicos finitos pertenecen a Q (son números racionales)
---------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------
b2) No periódicos: Un número decimal no periódico es aquel que tiene infinitas cifras decimales y estos no siguen una periodicidad, sino que progresan arbitrariamente. Por ejemplo las raíces cuadradas no exactas de los números entero positivos:
; ó el número 
(pi); ó el número 
(fi); ó el número e,…
Los números decimales no periódicos no pertenecen a Q (no son números racionales, son números irracionales, I).
3,708 + 41,237 + 126,1421=
40,238 – 3,63 =
64,23 x 2,18 =
154,23 x 7,318 =
347,4 : 938 =
297 : 4,2 =
4,17 : 21,32 =
2,347 : 0,213 =
4,508 : 5,3 =
345,3 : 4,72 =
57,24 : 0,235 =
1,9837 : 0.012 =
REPRESENTACIÓN GRÁFICA. ORDENACIÓN EN Q
Los números racionales se pueden representar gráficamente en una recta; partimos de 0 y representamos a la derecha los enteros positivos y a la izquierda de 0, los enteros negativos. En las subdivisiones de cada intervalo representamos los números fraccionarios; para ello, dividimos un intervalo en tantas partes como indica el denominador y tomamos un número de estas partes igual al que indica el numerador.
Ejemplo: representemos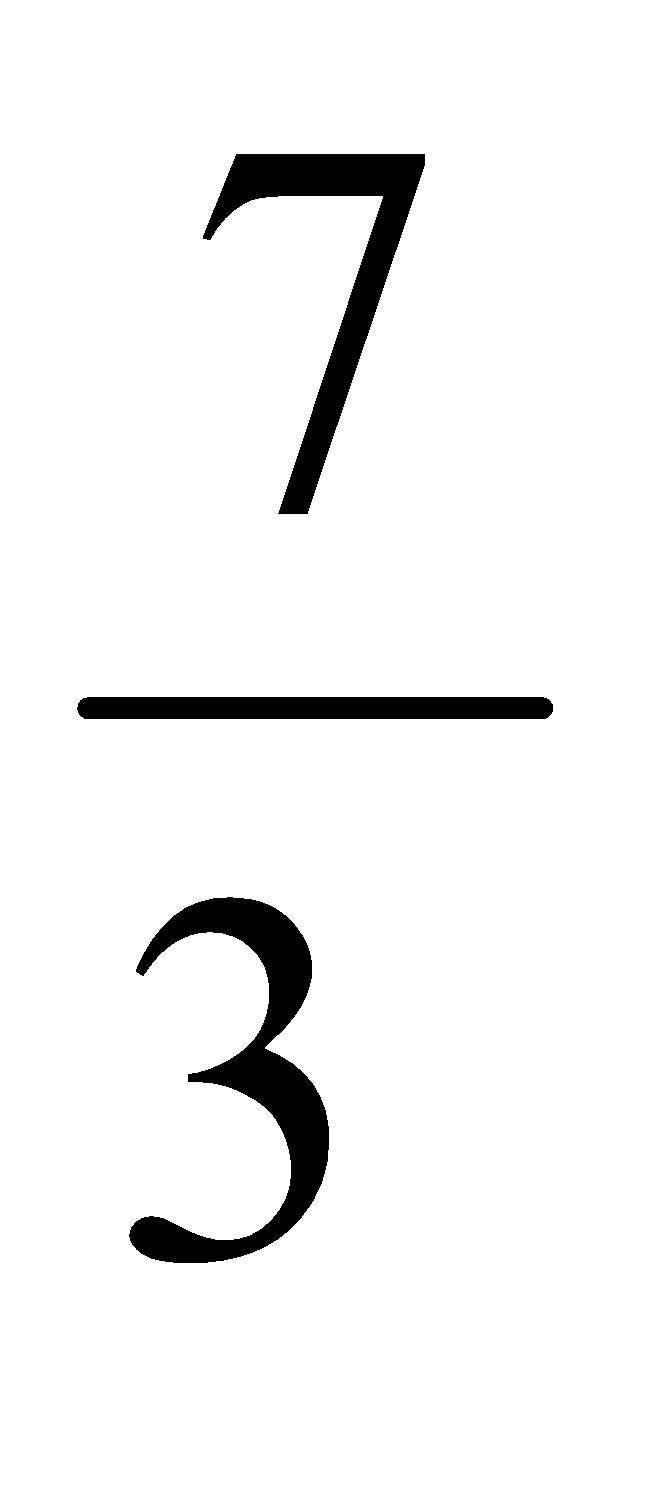 
y 
y
Esta recta, en la cual representamos los números racionales, se llama recta racional.
Entre cada dos números racionales cualesquiera, existen infinitos números racionales.
Podemos ordenar un conjunto finito de números racionales. Si algunos de estos números racionales que queremos ordenar tienen distinto denominador, por ejemplo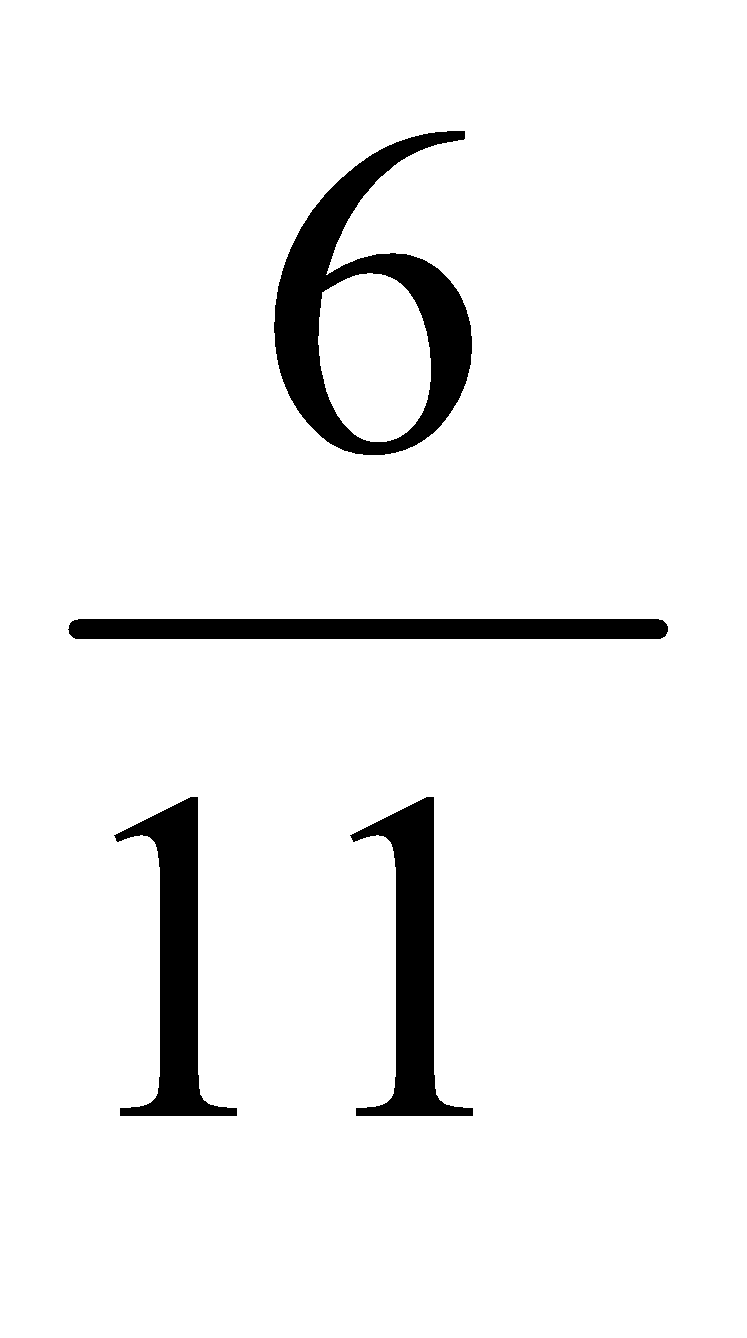 
y 
, ¿cuál es mayor? (Reducimos a común denominador, es decir, obtenemos fracciones equivalentes a las dadas pero con un denominador común y así, vemos claramente cuál es el mayor. Hagámoslo.
y 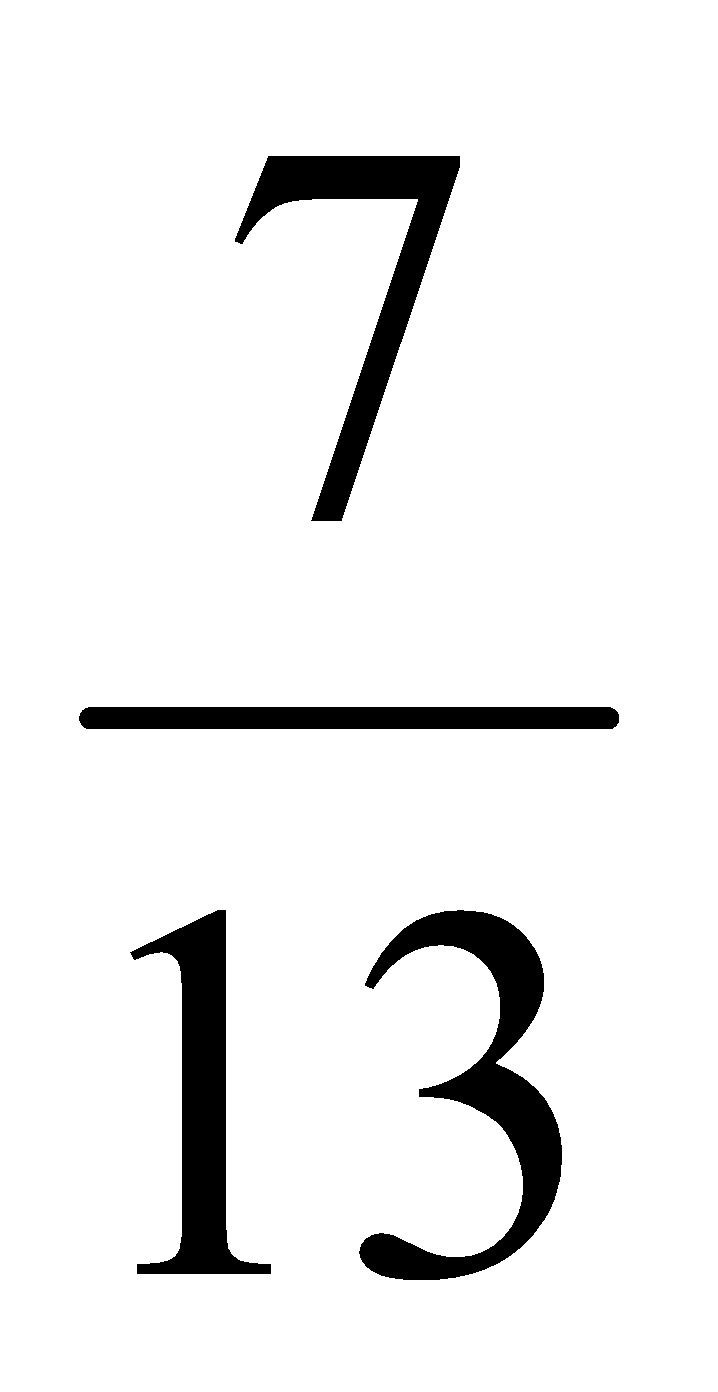, ¿cuál es mayor? (Reducimos a común denominador, es decir, obtenemos fracciones equivalentes a las dadas pero con un denominador común y así, vemos claramente cuál es el mayor. Hagámoslo.