PROBABILIDAD BINOMIAL. VARIABLE DISCRETA




Recuerda que en la estadística descriptiva vimos y representamos algunas distribuciones de frecuencia de variables cuantitativas discretas y continuas mediante diagramas de barras e histogramas respectivamente en las que la altura de las barras (v. discreta) o el área de cada rectángulo (v. continua) eran proporcionales a la frecuencia.
En las distribuciones de probabilidad lo que representamos son probabilidades, no frecuencias donde
Cada es un número comprendido entre 0 y 1:  
La suma de todos los , es decir,
Y, si la variable es discreta, la distribución de probabilidad se representa mediante un diagrama de barras:
Parámetros de una distribución de variable discreta:
Media: μ = Σpi xi
Desviación típica: = = ,

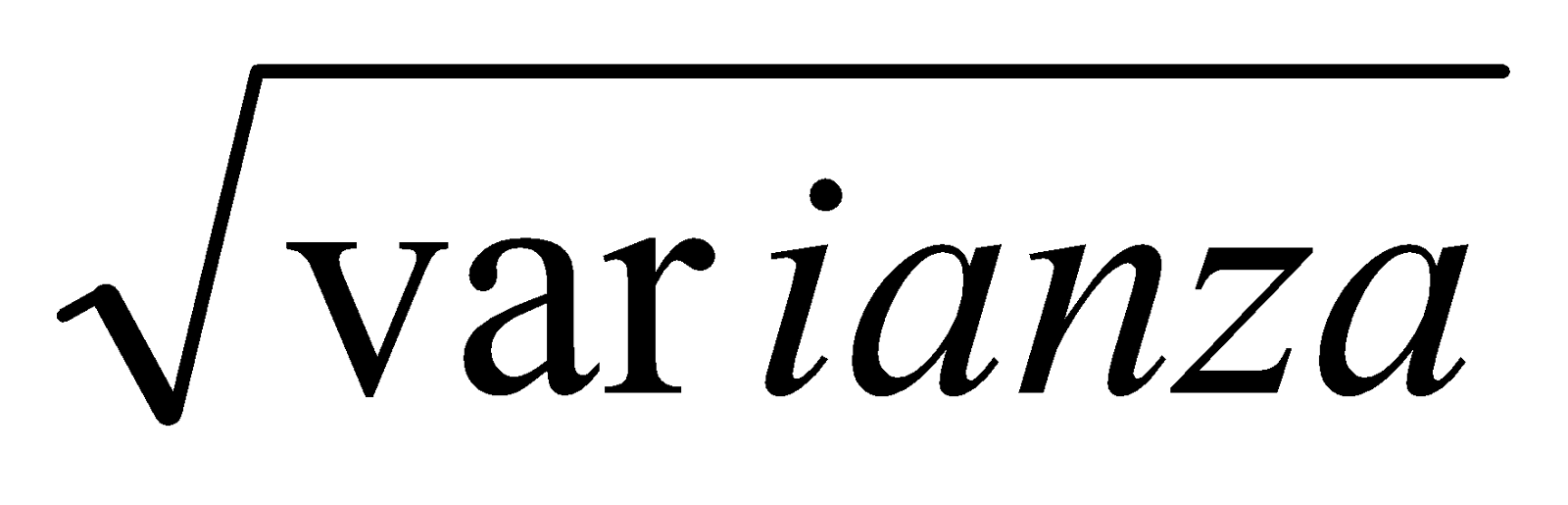Ej. 1: En una lotería popular hay 1 000 números. Se rifa un número, que gana 5 000 euros. El anterior y el siguiente ganan 1 000 €s cada uno. Todos los que tienen la misma terminación que el ganador se llevan 10 €, y el resto, nada. ¿Cómo se describe la probabilidad de premio de una persona que lleve un único número?




















  Media:


  Desviación típica:
LA DISTRIBUCIÓN BINOMIAL
El experimento de Bernoulli es un experimento de las siguientes características:
  • Solo definimos dos posibles resultados, sucesos: suceso A (éxito) y el suceso contrario o complementario, A´(fracaso).
  • El resultado obtenido en cada prueba (el experimento se realiza n veces) es independiente de los resultados anteriores.
  • La probabilidad del suceso A, p es constante y no varía de unas pruebas a otras.


Es decir, se repite n veces una misma experiencia dicotómica (solo dos posibles sucesos, éxito, fracaso). Nos preguntamos por el número, x, de éxitos (es decir, ¿P(x=a)?) . La variable x es discreta.
La distribución de probabilidad de este experimento recibe el nombre de distribución binomial de parámetros n y p y se expresa así:
B (n; p) donde:
 
p = P (A) es la probabilidad de éxito en cada una de las experiencias. Entonces,
q = P(A´) = 1 –p      y,
n es el número de veces que se repite la experiencia;

Y sus parámetros son:

Media :

Desviación típica:

¿Son los siguientes ejemplos distribuciones binomiales? Si lo son, define la distribución B (n; p) y calcula sus parámetros (μ y )
  1. Lanzamos 10 monedas y nos preguntamos por el número de caras.




  1. Lanzamos seis dados y nos preguntamos por el número de “cincos”.


  1. Dejamos caer al suelo 100 chinchetas y contamos cuántas caen con la punta hacia arriba. Suponemos que P (   ) = 0.3 y, por tanto P (   ) = ………



  1. Extraemos una carta de una baraja, observamos si es o no “figura”  y la devolvemos al mazo. Barajamos y volvemos a extraer. Repetimos cinco veces la experiencia (es decir, extraemos cinco cartas con reemplazamiento).



  1. Extraemos cinco cartas de una baraja y nos preguntamos cuántas figuras habrá.



  1. Nos preguntamos cuántos partidos ganará el Betis en sus próximos diez encuentros.


  1. Una máquina produce tornillos y, por término medio, un 2% son defectuosos. Se empaquetan en cajas de 100 tornillos. Nos preguntamos cuántos tornillos defectuosos habrá en cada caja.



CÁLCULO DE PROBABILIDADES EN UNA DISTRIBUCIÓN BINOMIAL
Ejemplo 2. Calcula la probabilidad de obtener “tres figuras” de una baraja española de 40 cartas cuando realizamos cinco extracciones con reemplazamiento.

  • ¿ es dicotómica la experiencia, es decir, en cada prueba del experimento son sólo posibles dos resultados?
  • ¿son independientes los resultados de cada prueba o experiencia?
  • ¿se mantiene constante la probabilidad p (y por tanto, q) de una prueba a otra?
  • En consecuencia, ¿es una distribución binomial? Defínela.
Entonces,:
n =
p=                  ; q =

P (tres figuras):      P(x=k) =         
Recuerda: 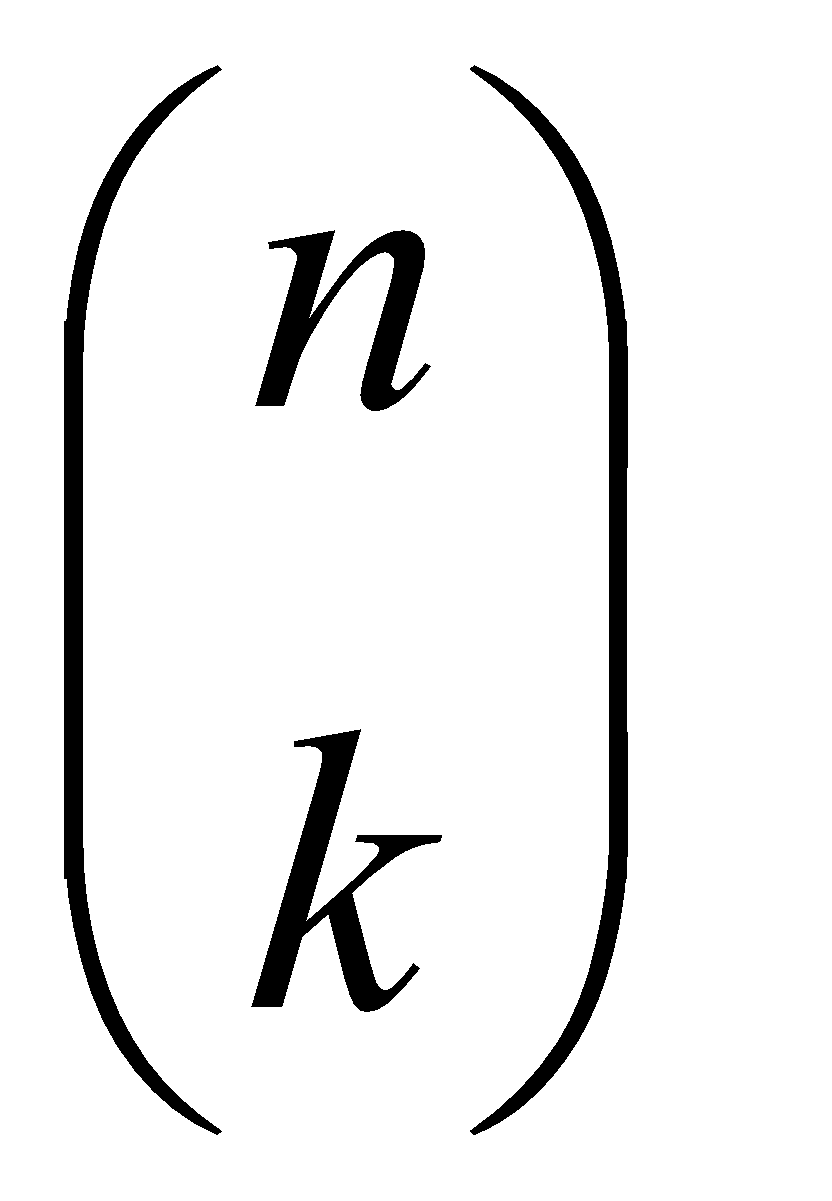  es un número combinatorio que se calcula así: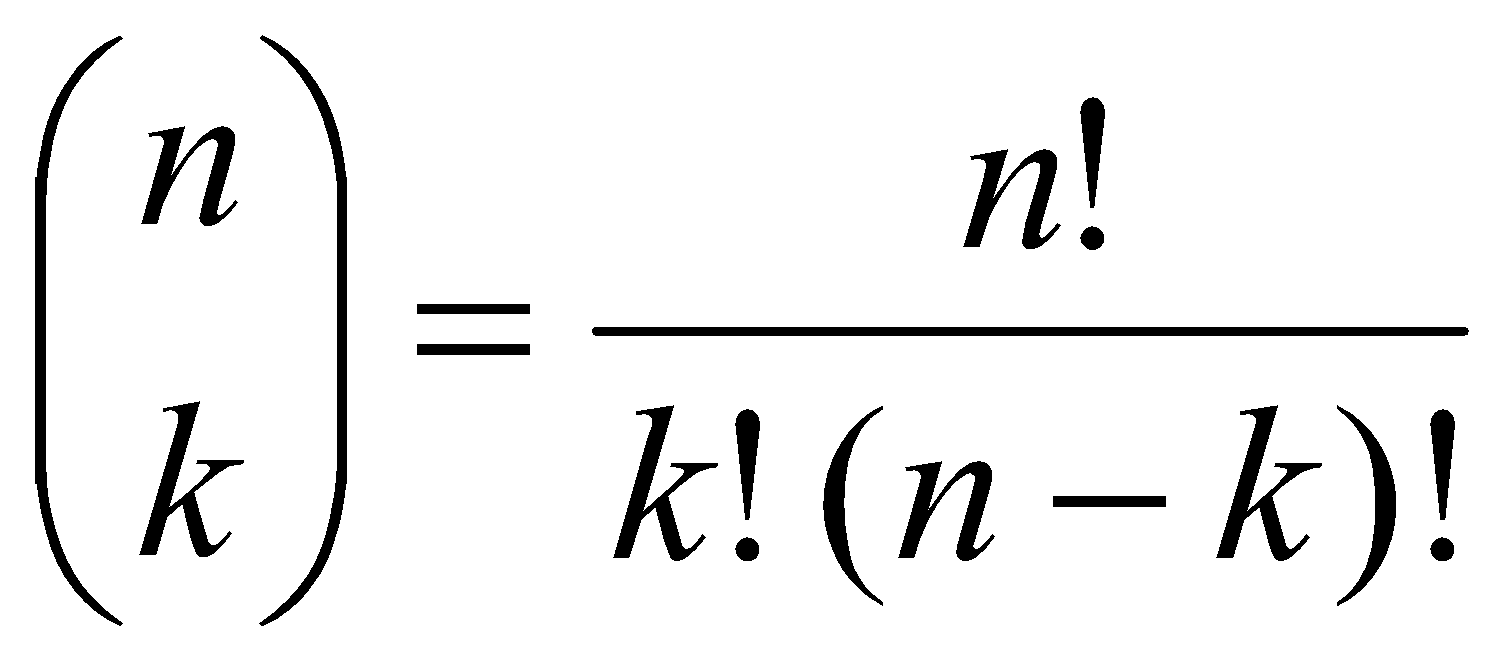





= =
  1. En una binomial B(8; 0.2), calcula P (x=0), P (x≠0), P (x=2), así como los parámetros y .







  1. En el proceso de fabricación de  bombillas, el 0.5% son defectuosas. Se comercializan en paquetes de 100. Hallar las probabilidades de que en un paquete haya:
  1. ninguna defectuosa.
  2. Alguna defectuosa.
  3. Dos defectuosas.
  4. Halla los parámetros y de esta distribución.
















  1. Lanzamos siete monedas. Calcula las probabilidades de 3 caras, 5 caras y 6 caras. Halla los valores de y













  1. La probabilidad de que una jugadora de golf haga hoyo en un lanzamiento a cierta distancia es 0.2. Si lo intenta cinco veces, calcula la probabilidad de que:
  1. no acierte ninguna.
  2. Acierte alguna.
  3. Acierte dos.
  4. Si hace tandas de 5 lanzamientos, ¿cuál será el número medio de aciertos? ¿Cuál será su desviación típica?












  1. Una máquina produce disquetes. Se ha comprobado que el 5% son defectuosos. Tomamos 10 disquetes al azar y nos preguntamos por el número de defectuosos:
a) ¿Es una distribución binomial?         Defínela.
b) Calcula sus parámetros y .
c) Calcula P(x=0),  P(x>0),  P (x=2)














  1. Calcula la probabilidad de que en una familia cualquiera de 4 hijos, 3 de ellos sean varones. Define la distribución y halla su media y desviación típica.









  1. Se lanzan tres monedas y se cuenta el número de caras que salen. Calcula la probabilidad de obtener:

  1. una cara.
  2. Más de una cara.
  3. Tres caras.
Suscribirse a: Entradas (Atom)