La distribución normal es una distribución de probabilidad de variable aleatoria continua (puede tomar infinitos valores dentro de un intervalo de la recta real).
Su importancia reside en la enorme frecuencia con que aparece en las situaciones más variadas:
- Caracteres morfológicos de individuos (personas, animales, plantas,…) de una misma raza. Por ejemplo: tallas, pesos, envergaduras, …
- Caracteres fisiológicos. Por ejemplo, efectos de una misma dosis de un fármaco o de una misma cantidad de abono.
- Caracteres sociológicos. Por ejemplo, consumo de ciertos productos por individuos de un mismo grupo humano.
- Caracteres físicos. Por ejemplo, resistencia a la rotura de piezas aparentemente idénticas; duración de las bombillas de una marca y modelo.
Y, en general, cualquier característica que se obtenga como una suma de muchos factores.
En el caso de variables aleatorias continuas no tiene sentido plantearse probabilidades de resultados aislados, por ejemplo, probabilidad de que una bombilla dure 100 horas, 22 minutos y 16 segundos. La probabiladad de un resultado concreto es 0.
El interés de estas probabilidades está en conocer la probabilidad correspondiente a un intervalo. Dicha probabilidad se conoce mediante una curva llamada función de densidad y suponiendo que bajo dicha curva hay un área de una unidad (Área debajo de la curva =1).
Así que conociendo esta curva, basta calcular el área correspondiente para conocer la probabilidad de un intervalo cualquiera.
Entonces:
- Es necesario que la curva no sea negativa.
- El área total bajo la curva es igual a 1.
- Las probabilidades de sucesos puntuales son cero: P(x=a) = 0, P(x=b) = 0, …
Por tanto, P(a 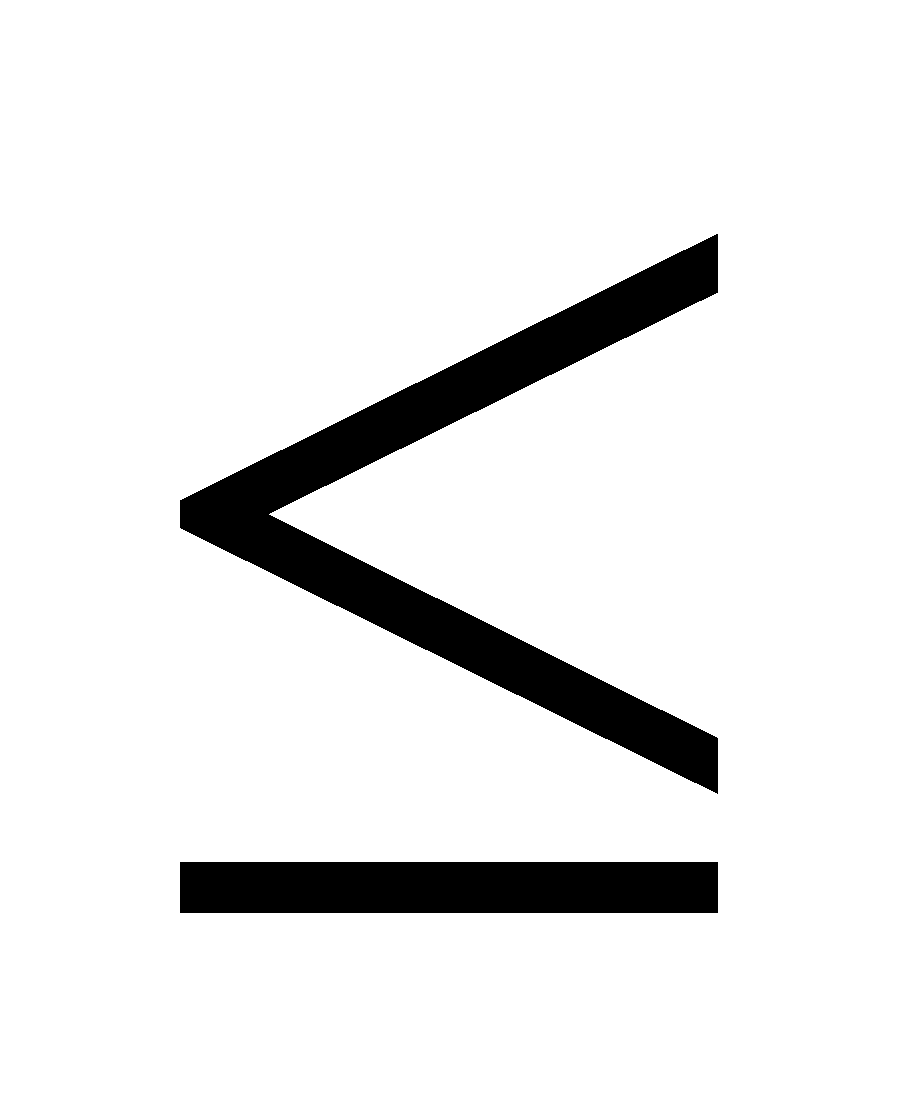 x
x 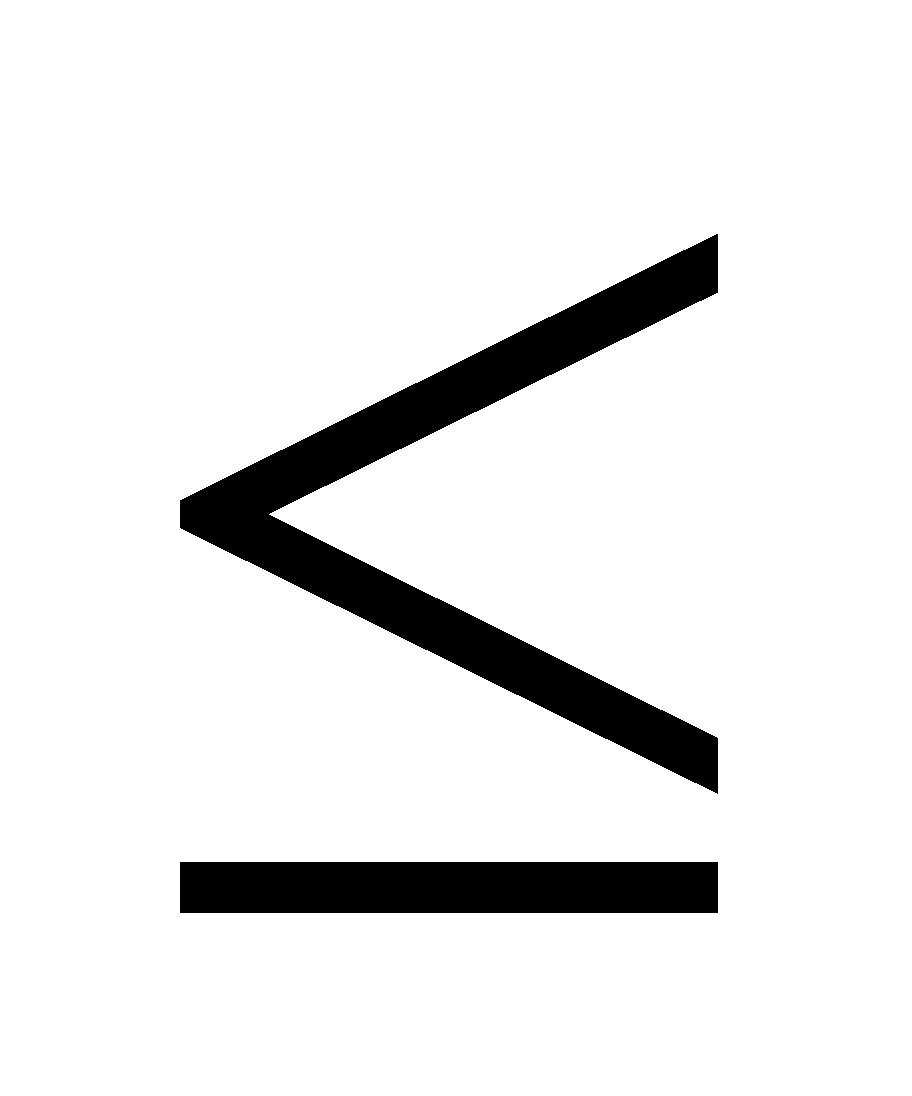 b) = P (a< x< b)
b) = P (a< x< b)
La campana de Gauss , curva de Gauss o curva normal, es una función de probabilidad continua, simétrica, cuyo máximo coincide con la media,  de la distribución.
de la distribución.
Para cada valor de  (media) y cada valor de
(media) y cada valor de  (desviación típica), hay una curva normal, que se denomina N (
(desviación típica), hay una curva normal, que se denomina N ( ,
,  ).
).
CÁLCULO DE PROBABILIDADES EN UNA DISTRIBUCIÓN N (0, 1):
- Si k
0, las probabilidades P(z
k) = P(z < k) =
(k) se encuentran directamente en las tablas (positivas).
- P (z
k) = 1 – P(z < k) = 1 -
(k)
- Para abscisas negativas, P (z
-k) = P (z
k) = 1 -
(k)
- Las restantes probabilidades se pueden obtener a partir de estas.
- Halla las siguientes probabilidades(en tablas positivas y tablas negativas):
a) P (z< 1.35) b) P(z< -0.338) = P (z< -0.34) c) P (z> 2.1)
d) P (z>-1) e) P(-1.39 < z 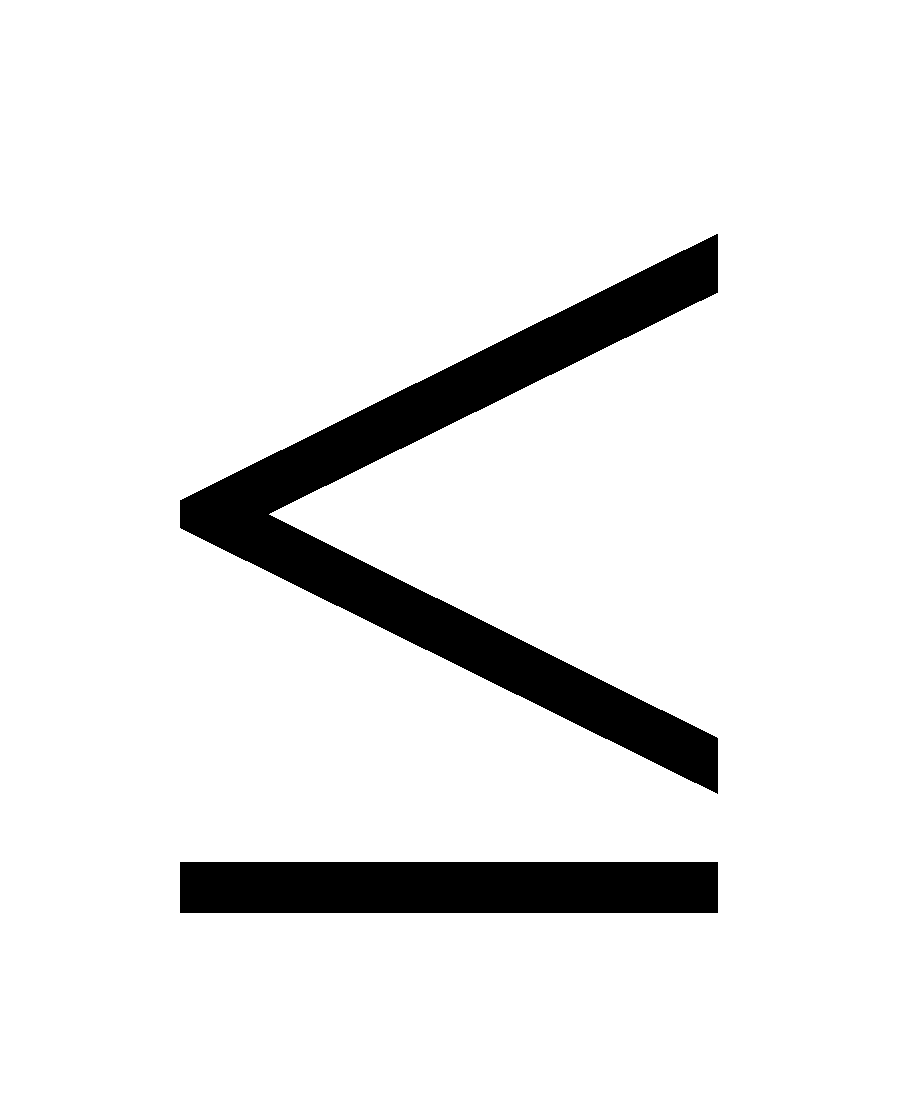 -0.44) f) P (-1.52
-0.44) f) P (-1.52  z
z 0.897)
0.897)
CURVA NORMAL
Como decíamos, gran número de distribuciones tienen la forma de una campana; es decir, alejándonos de la media, a derecha e izda , el número de observaciones decrece de forma similar . Esto genera una curva simétrica.
La ecuación de esta curva está en función de la media y desviación típica de la distribución.
Ante las infinitas posibles medias y desviaciones, hay una infinidad de posibles distribuciones normales pero el proceso de tipificación, permite reducirlas a una única con media 0 y desviación típica 1, es decir, N (0; 1).
Como los valores de las áreas bajo la curva normal se encuentran tabulados con referencia a la normal tipificada N (0: 1) nos vemos obligados a tipificar previamente cualquier otro tipo de distribución normal que deseemos estudiar.
Tipificación de una distribución N ( ;
; ) cualquiera:
) cualquiera:
Si x es la variable de una distribución N ( ;
; ), para calcular la probabilidad P (h< x< k) se procede así:
), para calcular la probabilidad P (h< x< k) se procede así:
P (h< x< k) = 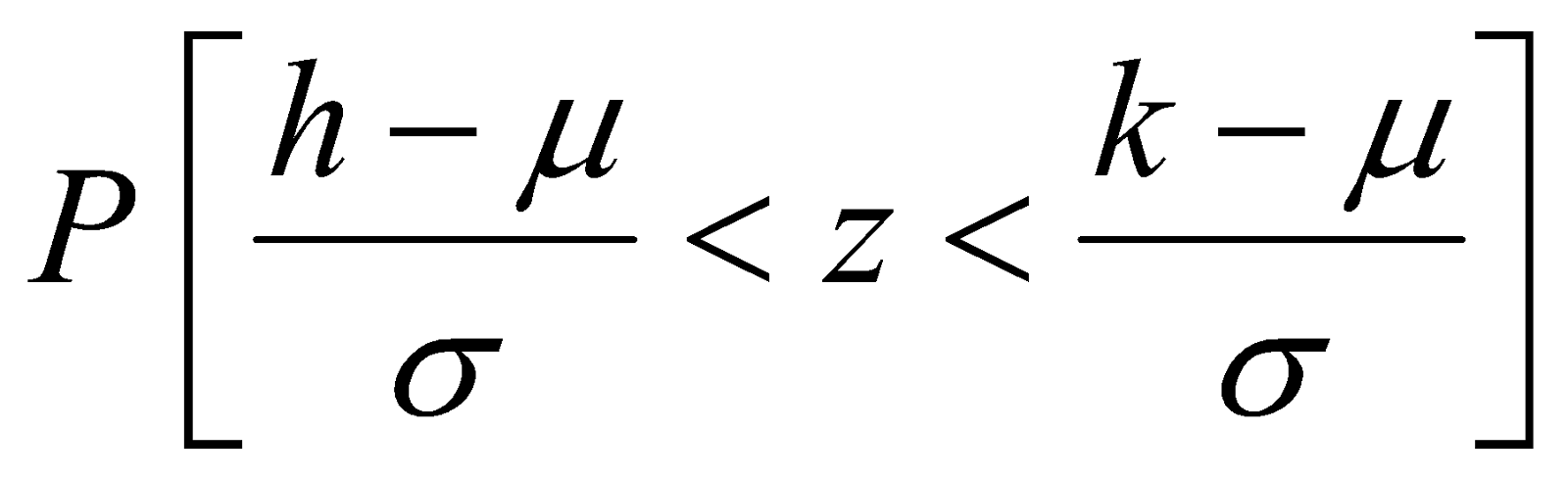
Llamamos x a la variable de una distribución N ( ;
; ) cualquiera y z a la variable de la distribución N(0; 1). Así lo haremos siempre.
) cualquiera y z a la variable de la distribución N(0; 1). Así lo haremos siempre.
- En una N (6; 4) calcula las probabilidades siguientes:
a) P (x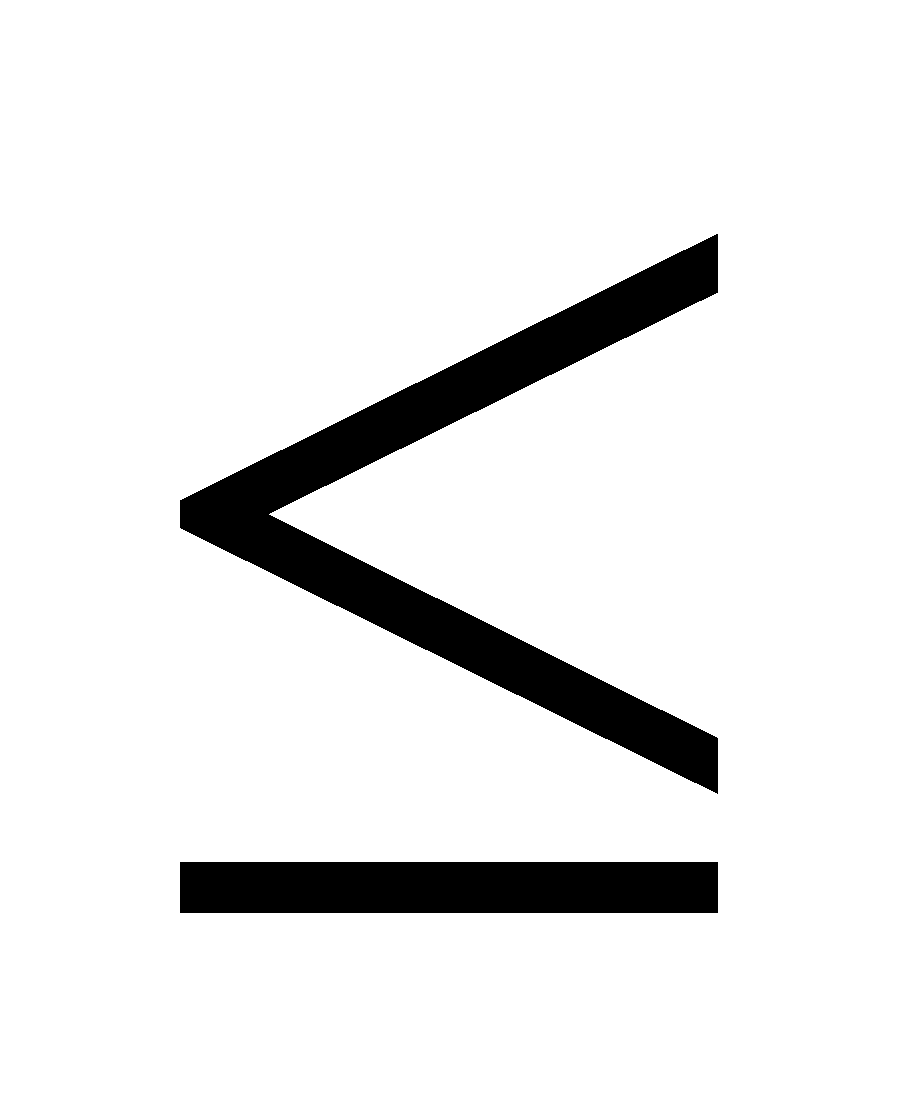 3) b) P (x
3) b) P (x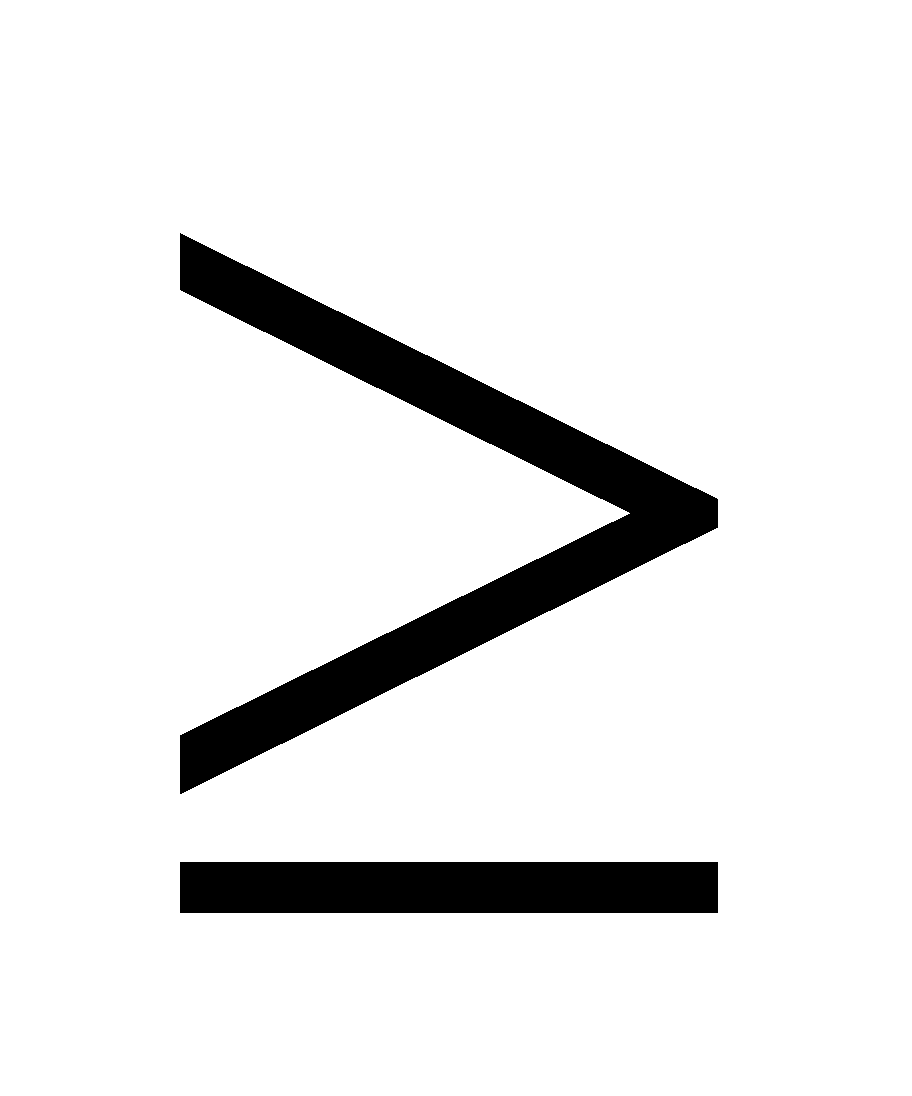 12) P (5
12) P (5 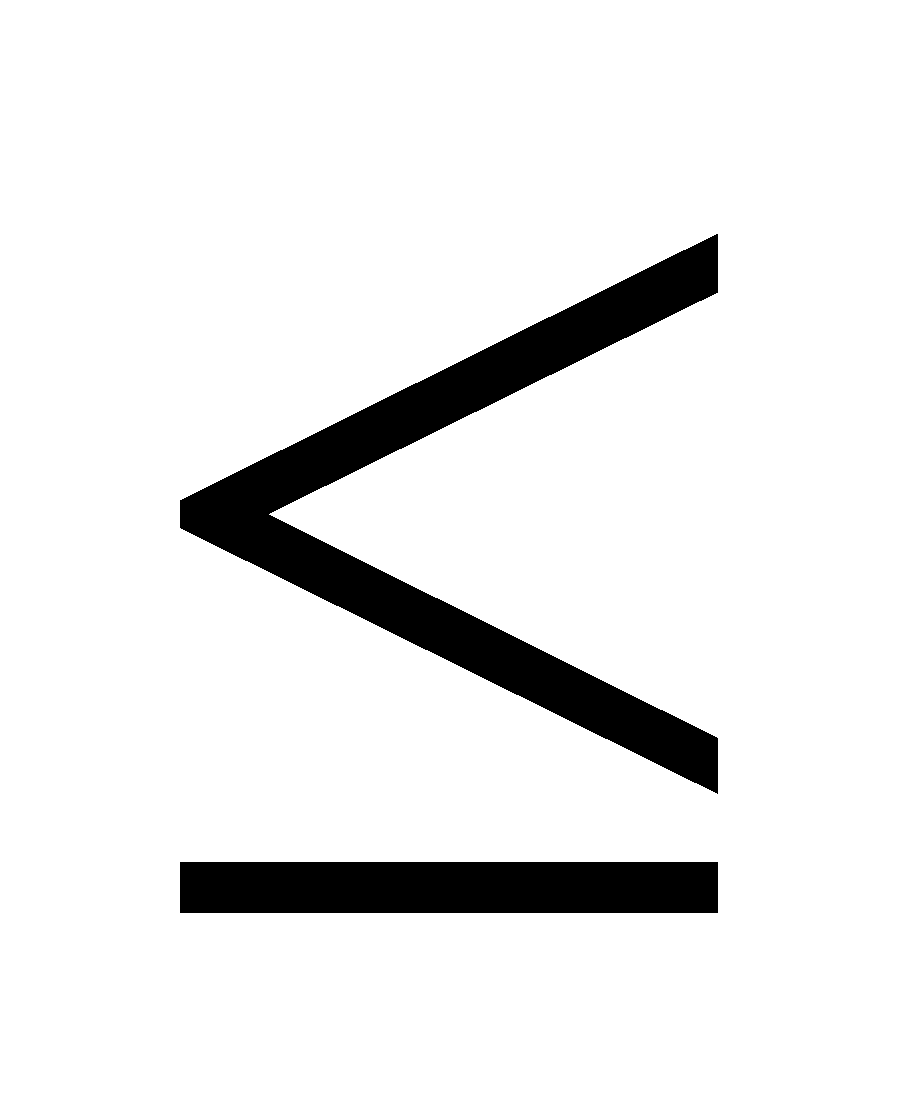 x
x 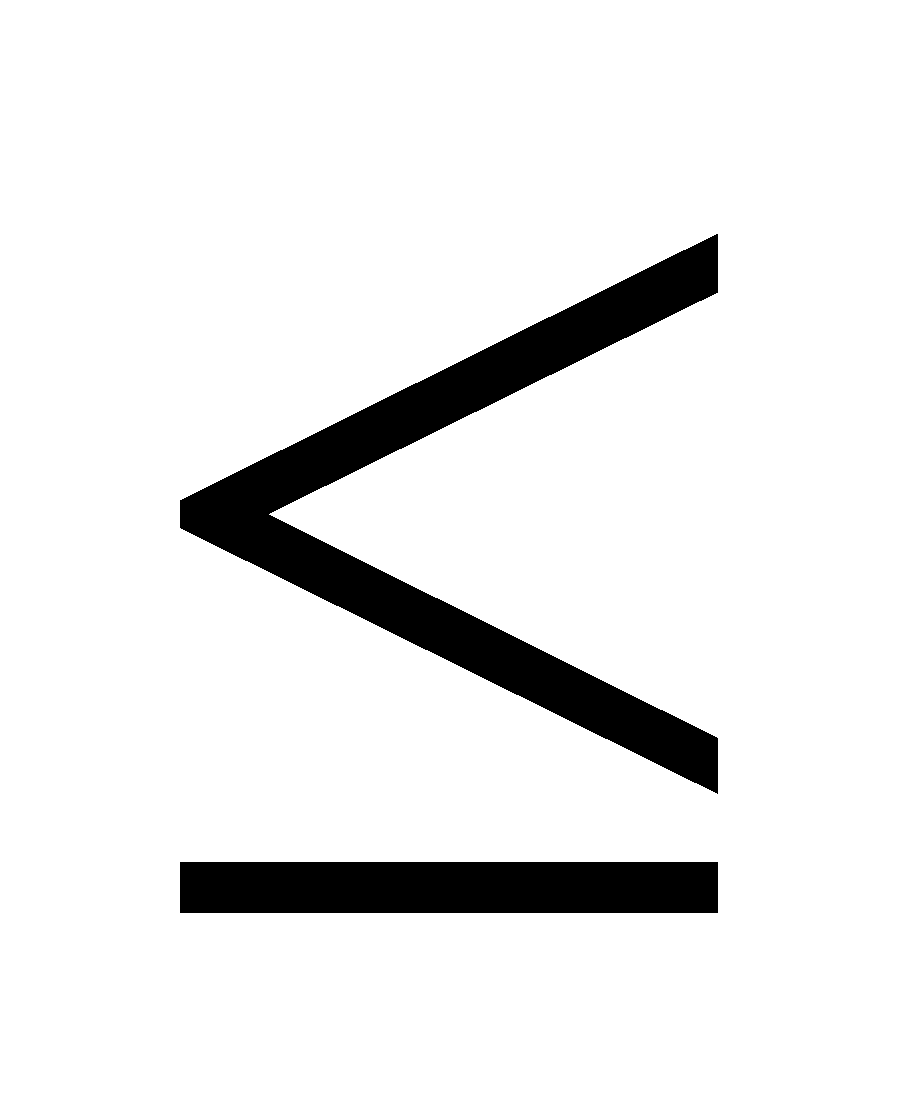 8)
8)
- Las calificaciones de los 500 aspirantes presentados a un examen para contratación laboral, se distribuye normalmente con media 6.5 y varianza 4.
- Calcula la probabilidad de que un aspirante obtenga más de 8 puntos.
- Determina la proporción de aspirantes con calificaciones inferiores a 5 puntos.
- ¿Cuántos aspirantes obtuvieron calificaciones comprendidas entre 5 y 7.5 puntos?
- Analizadas 240 determinaciones de colesterol en sangre, se observó que se distribuían normalmente con media 100 y desviación típica 20.
- Calcula la probabilidad de que una determinación sea inferior a 94.
- ¿Qué proporción de determinaciones tienen valores comprendidos entre 105 y 130?
- ¿Cuántas determinaciones fueron superiores a 138?
- Los 460 alumnos de un centro tienen 156 cm de estatura media con una varianza de 81 cm.
- Determina el porcentaje de alumnos que miden más de 160 cm.
- ¿Cuántos alumnos miden entre 140 y 150 cm?
- Las edades de un grupo de 320 individuos tienen como media 24 y desviación típica 5. ¿Cuántos tendrán menos de 27 años?
- El peso de los individuos de una población se distribuye normalmente con media de 70 kg y desviación típica 6 kg. De una población de 2000 personas, calcula cuántas tendrán un peso comprendido entre 64 y 76 kg.
- Las estaturas de los individuos de una población se distribuyen normalmente con media 175 cm y desviación típica 10 cm. Calcula la probabilidad de que:
- Un individuo tenga una estatura mayor que 180 cm.
- Un individuo tenga una estatura menor que 170 cm.
- ¿Qué proporción de individuos tiene una estatura comprendida entre 170 cm y 180 cm?
APROXIMACIÓN DE LA DISTRIBUCIÓN BINOMIAL MEDIANTE LA NORMAL.
Cuando n es grande (mayor que 10) y p está próximo a 0.5, el comportamiento de una distribución binomial B(n; p) es aproximadamente igual a una distribución normal de media np y desviación típìca 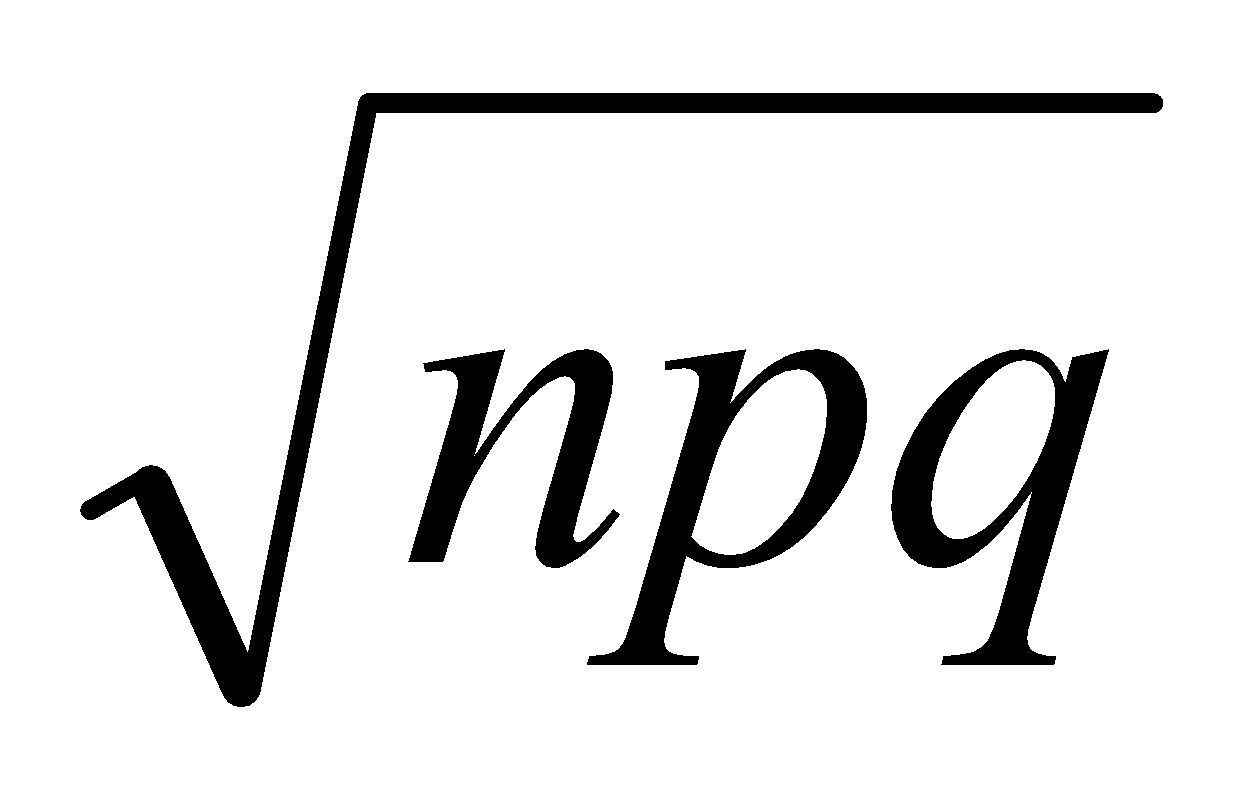 ; es decir, N (np;
; es decir, N (np; 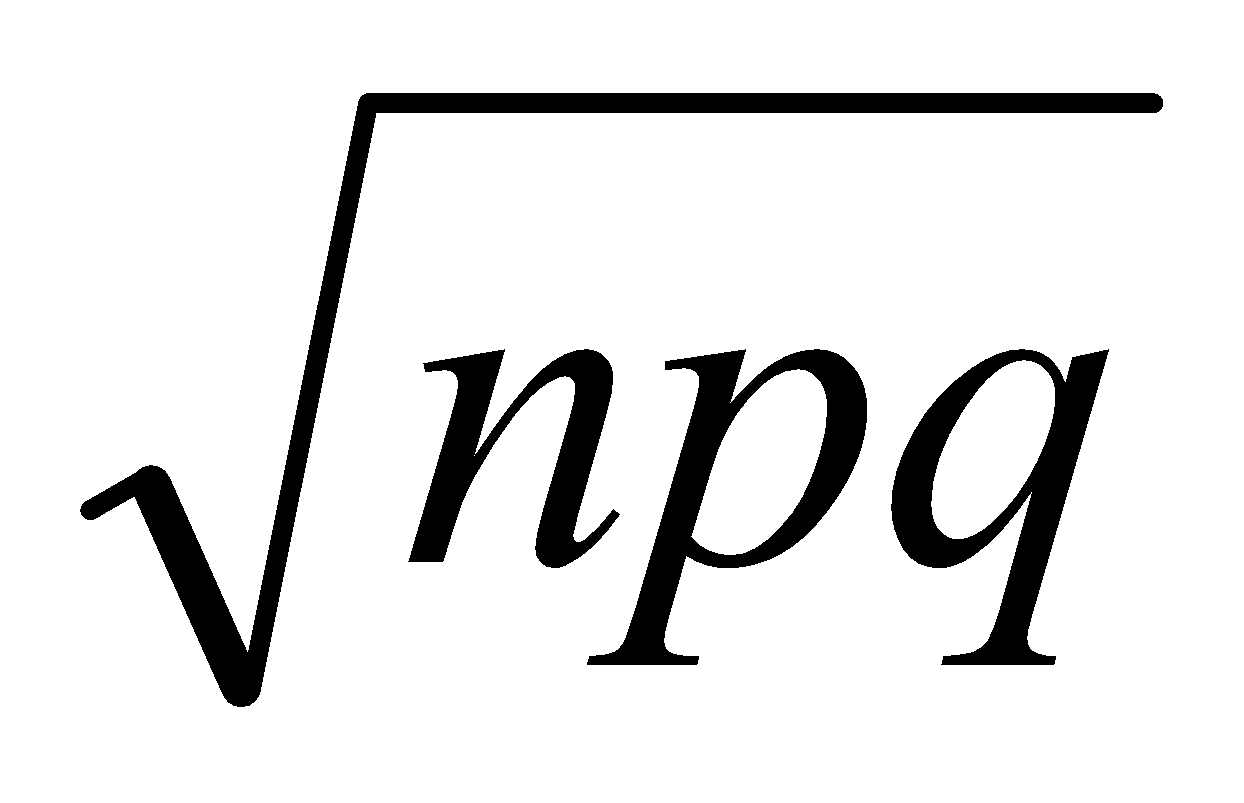 ).
).
Esto permite sustituir el estudio de una B(n; p) por el de una N (np; 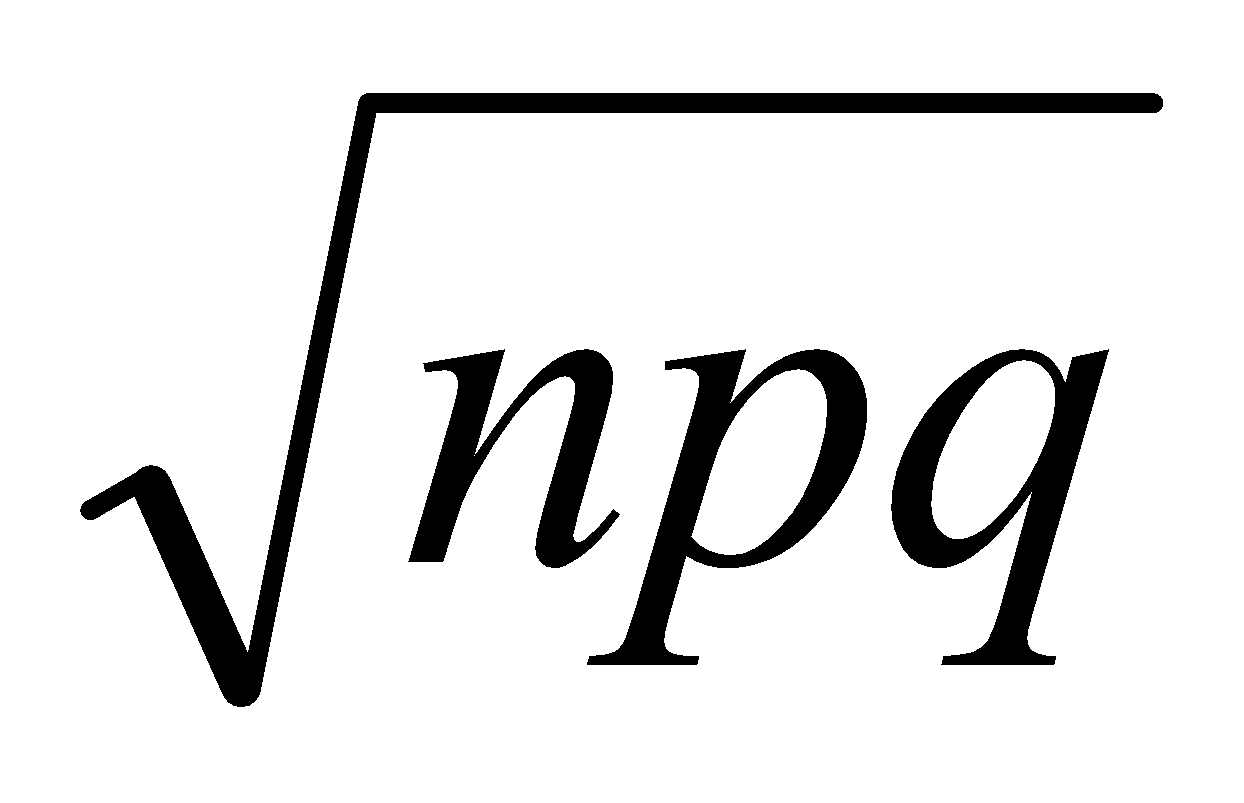 ).
).
Se considera que la aproximación es buena cuando np > 5 y nq > 5.
- Se lanza una moneda correcta al aire 400 veces. Calcula la probabilidad de obtener un número de caras comprendido entre 180 y 210, ambos inclusive.
- El 2% de los tornillos fabricados por una máquina presentan defectos. En un lote de 2000 tornillos, ¿Cuál es la probabilidad de que haya menos de 50 defectuosos?
- Calcula la probabilidad de que la variable de la distribución binomial B (50; 0.6) valga 32, 33, 34, 35, 36 ó 37.
CORRECCIÓN DE YATES
Dado que por mucho que se parezca nunca es igual una binomial que una normal, es necesario aplicar en el cálculo de probabilidades un ajuste que recibe el nombre de corrección de Yates.
Si x es la binomial y x´la normal, la corrección consiste en:
Esta corrección no la haremos en bachiller, si no se nos pide expresamente ya que en la tipificación de una binomial a una normal hecha anteriormente, aunque se comete un pequeño error, este error es despreciable salvo si n es excesivamente pequeño (n<10).
Para valores de n mayores de 1000 se puede suprimir la corrección.
- Un tirador acierta en el blanco en el 70% de los tiros. Si el tirador participa en una competición y tira 25 veces, ¿Cuál es la probabilidad de que acierte más de 10 tiros?
- Un torno mecaniza tornillos, de los cuales, por experiencias anteriores se sabe que un 0.3 % presentan algún pequeño defecto. Estos tornillos se comercializan en cajas de 1000 unidades. Si se toma una caja al azar, ¿cuál es la probabilidad de que contenga 1, 2, 3, 4, 5 ó 6 tornillos defectuosos?