ESTADISTICA GENERAL

CONCEPTOS GENERALES
Estadística: Ciencia para la obtención, estudio e interpretación de grandes masas de datos. Analiza series de datos (por ej, edad de una población, altura de estudiantes de una escuela, temperatura en los meses de verano,…) y trata de extraer conclusiones sobre el comportamiento de esas variables.
Estadística unidimensional: estudia el “comportamiento” de una única variable en una población.
Población: Conjunto de todos los elementos (individuos) que portan información sobre el fenómeno que se estudia y que serán objeto de nuestro análisis (alumnos de un colegio, total de viviendas de una ciudad,…)
Muestra: Subconjunto extraído de la población, cuyo estudio sirve para inferir (obtener consecuencias, conclusiones) características de toda la población. Por ejemplo, si estudiamos el precio de la vivienda en una ciudad, los normal será no recoger información sobre todas las viviendas de la ciudad (labor muy compleja y costosa) sino que se selecciona un subgrupo (muestra) que se entiende suficientemente representativo.
Individuo: Cada uno de los elementos que forman la población  o la muestra y porta información sobre el fenómeno que se estudia. Así, si estudiamos la altura de los niños de una clase, cada alumno es un individuo; si estudiamos el precio de la vivienda en una ciudad, cada vivienda es un individuo.
Variable estadística: carácter, característica que se desea analizar y que toma distintos valores.
.
  • Variables cualitativas. NO toman valores numéricos (nacionalidad, color del pelo, sexo,…)
  • Variables cuantitativas DISCRETAS: toman valores numéricos discretos, enteros, aislados. (número de hijos, cantidad de aprobados, edad, precio de un producto, ingresos anuales…)
  • Variables cuantitativas CONTINUAS: Pueden tomar cualquier valor real de un intervalo. (estatura, peso, velocidad de un vehículo…). También se tratan como variables continuas las variables discretas cuyo número de datos sean tan grandes que las variaciones unidad a unidad respecto del total sean insignificantes (p.ej.: ingresos anuales de los habitantes de los habitantes de un país)
DISTRIBUCIONES ESTADÍSTICAS
Frecuencia: número de veces en que la variable toma un valor determinado, es decir, número de veces que se repite un valor de la variable, por ejemplo, número de alumnos que miden 1.67 m en un colegio.
La distribución de frecuencia es la representación estructurada, en forma de tabla, de toda la información recogida sobre la variable que se estudia.
Ejemplo: altura de los niños de una clase. Resultados de la medición (m): 1.25; 1.28; 1.27; 1.21;… Se ordenan los datos y se realiza la tabla xi  fi
Parámetros estadísticos: Valores numéricos obtenidos a partir de los datos de la variable y que sirven para sintetizar la información dada por una tabla estadística. (media, mediana, moda, desviación típica,…).

REPRESENTACIÓN DE DISTRIBUCIONES ESTADÍSTICAS
Estudiemos algunas distribuciones de frecuencias de variables cuantitativas (numéricas):
Si la variable es DISCRETA se representa la distribución de frecuencias mediante barras estrechas situadas sobre los valores de la variable y separadas unas de otras: diagrama de barras. (Las alturas de las barras son proporcionales a las frecuencias).
Si la variable es CONTINUA los individuos que hay en cada intervalo pueden tener valores situados en cualquier punto del mismo. Se representa la distribución de frecuencias mediante rectángulos que ocupan todo el intervalo: histograma. (Cuando el ancho de las distintos rectángulos no es el mismo, lo que marca la frecuencia no es la altura sino el área del rectángulo)


  1. Representa la siguiente distribución correspondiente a la población de un cierto país en el año 2007:
EDAD (años)
Nº HABITANTES
(millones)
1.8
2
2
2.6
3.2
3.5
6
5.3
3.6
3
1
¿Cuál es la variable? ¿De qué tipo es?













TABLAS DE FRECUENCIAS
Tablas con datos aislados
Las tablas de frecuencia sirven para ordenar y organizar los datos estadísticos. Así una masa amorfa de datos pasa a ser una colección ordenada e inteligible.
  1. Construye la tabla de frecuencias para los datos adjuntos: Se ha realizado una encuesta a 50 matrimonios de una cierta barriada. Entre las preguntas que se les hicieron figuraba el número de hijos. Estas son las respuestas:

2  2  0  3  1          2  3  3  3  2          1  2  2  1  3           2  3  3  1  4
2  4  3  1  3          2  4  2  2  3          1  2  3  3  2           3  2  4  1  3
3  3  2  2  3         3  1  5  2  0           
Con estos datos realiza la tabla: Variable xi (número de hijos). Frecuencia: fi (veces que se repite cada dato) Fi (frecuencia acumulada: F1= f1; F2 = f1+f2; F3 = f1+f2+f3; …             
¿Cuál es la variable? ¿De qué tipo es?






Tablas con datos agrupados en intervalos
  • Cuando en una distribución estadística el número de valores que toma la variable es muy grande, conviene elaborar una tabla de frecuencias agrupándolos en intervalos.

El punto medio de cada intervalo se llama marca de clase. Es el valor que representa a todo el intervalo para el cálculo de algunos parámetros y también para representar el polígono de frecuencias o diagrama de líneas.

  • Se incluye la columna de marcas de clase (xi) en la tabla.
  1. Medimos la estatura de los habitantes de un bloque de viviendas y obtenemos los siguientes resultados (m):

1.15   1.48   1.57   1.71   1.92             1.39   1.40   1.64   1.77   1.49                   1.53   1.16   1.60   1.81   1.98             1.20   1.42   1.45   1.20   1.98  
1.21   1.59   1.86   1.52   1.48             1.37   1.16   1.73   1.62   1.01   
 
El número de intervalos en los que se agrupa la información es decisión del analista; la regla es que cuantos más intervalos menos información se “pierde” , pero puede que menos representativa e ilustrativa del fenómeno estudiado sea la tabla. (El número de intervalos no debe ser inferior a 6 ni superior a 15).
Con estos datos realiza la tabla: xi,  fi,  Fi                 
¿Cuál es la variable? ¿De qué tipo es?













PARÁMETROS ESTADÍSTICOS
Parámetro: Medidas calculadas a partir de los datos obtenidos.
  • Parámetros de centralización: nos indican en torno a qué valor, centro, se distribuyen los datos. Son parámetros de centralización: mediana, moda y media.
Moda: de un conjunto de datos es el dato (xi) que tiene mayor frecuencia.
Mediana: Si los individuos de una población están colocados en orden creciente según la variable que se estudia y partimos la población en dos trozos con el mismo número de individuos, entonces la mediana es el valor de la variable (xi) que supera al 50% de los individuos.
Mediana de un conjunto ordenado de datos es aquel valor tal que la mitad de los datos son iguales o inferiores a él y la otra mitad son iguales o superiores.

Caso 1: Cuando el número de datos es impar: Mediana:
Si los valores son 4,6,4,5,7,3,9. Los ordenamos 3,4,4,5,6,7,9, como son 7 datos cogemos el dato que ocupa el lugar 4º que es 5. Mediana (Me): 5



Caso 2: Cuando el número de datos es par: Mediana:
Si los valores son 4,6,5,7,3,9. Los ordenamos 3,4,5,6,7,9, como son 6 datos cogemos los datos que ocupan  el lugar 3º que es 5 y el lugar 4º que es 6. la mediana es la media de los dos números es este caso 5,5 =(5+6)/2



Media: valor medio “ponderado” de la serie de datos (se tiene en cuenta la cantidad de veces, fi , que aparece cada dato).

Media aritmética: producto de cada valor de la variable por el número de veces que se repite.  
  • Parámetros de dispersión: informan sobre cuánto se alejan del centro los valores de la distribución. Son parámetros de dispersión: desviación típica, varianza.  
CÁLCULO E INTERPRETACIÓN de la MEDIA  y la DESVIACIÓN TÍPICA
MEDIA: La media es el centro de gravedad de la distribución. Es decir, si las barras del diagrama de barras (o los rectángulos de los histogramas) tuvieran peso, la media es el punto donde habría que sostener la tablilla en que se sitúan.

DESVIACIÓN TÍPICA: σ =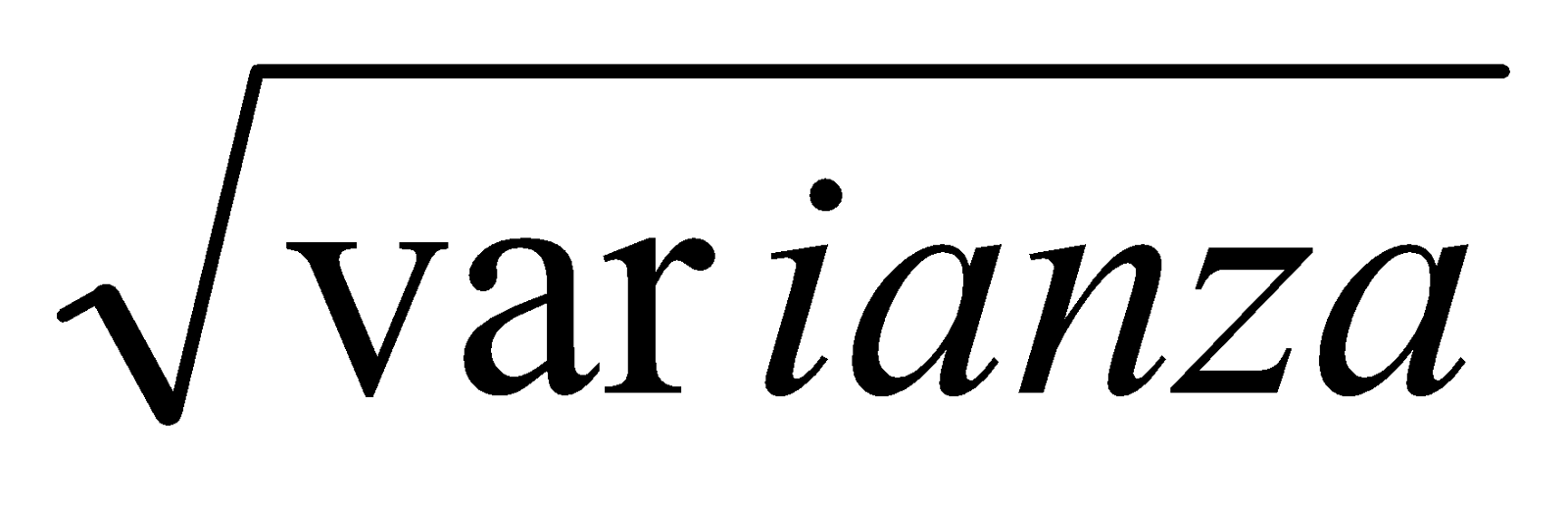

Si la varianza es   σ2 = , entonces,

la desviación típica es σ = 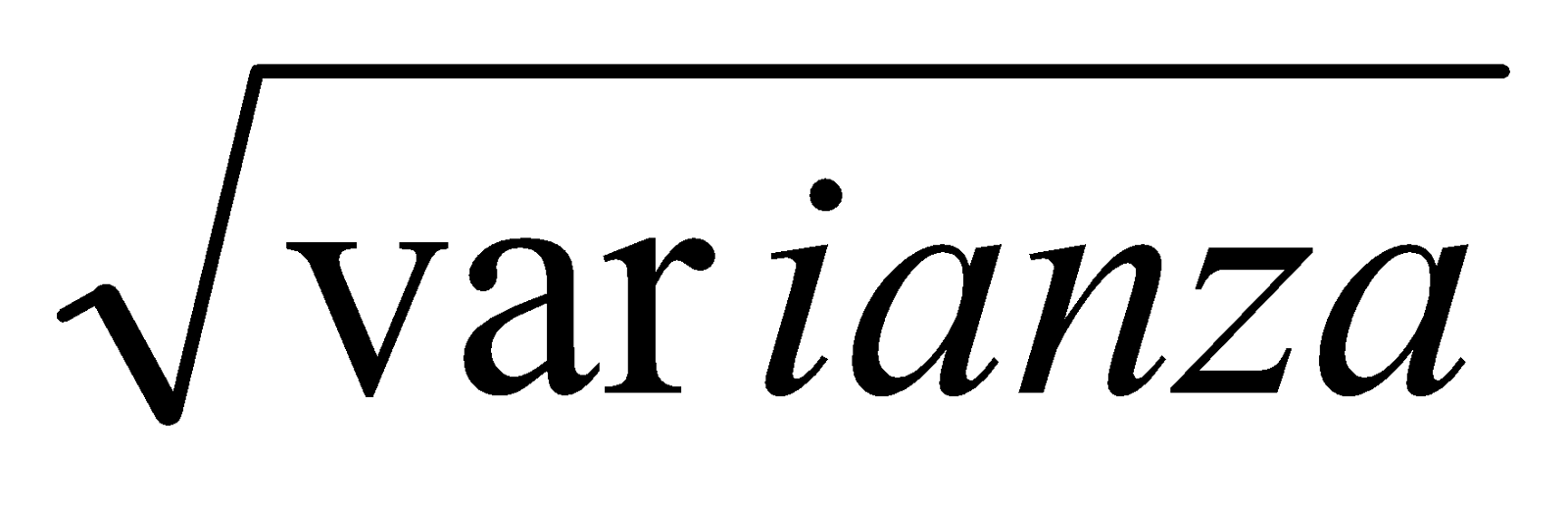La desviación típica nos dice cómo de alejados, dispersos, están los datos de la distribución respecto de la media.
    Cuánto mayor es σ , más dispersos, más alejados están los datos de la media.
  1. Calcula la media y desviación típica de los datos de la estatura de los alumnos de la página 4 de estos apuntes.
¿Cuál es la variable? ¿De qué tipo es?


















;  σ = 0.25 m
  1. Calcula , σ y C.V. en la distribución dada en la tabla adjunta relativa a las pulsaciones por minuto de estudiantes de mecanografía:
Indica también cuáles son la mediana y la moda.
Fi
151
2



156
4



161
11



166
14



171
5



176
4



Coeficiente de variación: C.V. =
¿Cuál es la variable? ¿De qué tipo es?













Sol: 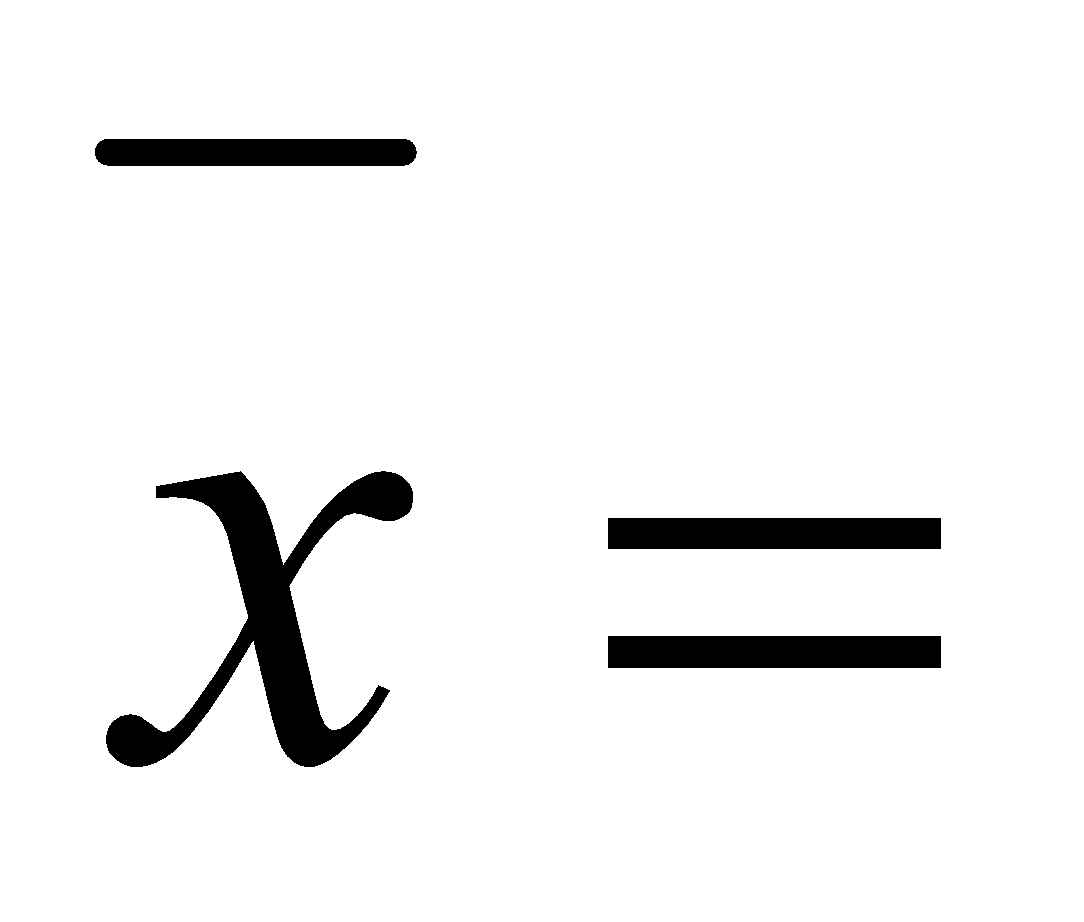164.5 puls; Me=166;
Mo = 166; σ = 6.224 pulsaciones CV = 0.038
  1. Calcula , σ y C.V. en la siguiente distribución: tiempo que emplean un grupo de alumnos en ir de su casa al colegio (Recuerda: al intervalo le corresponde el valor de marca de clase, es decir, 2.5)
Tiempo (min)
Marca de clase (xi)
Nº de alumnos
 
 

2




11




13




6




3




1





Sol: 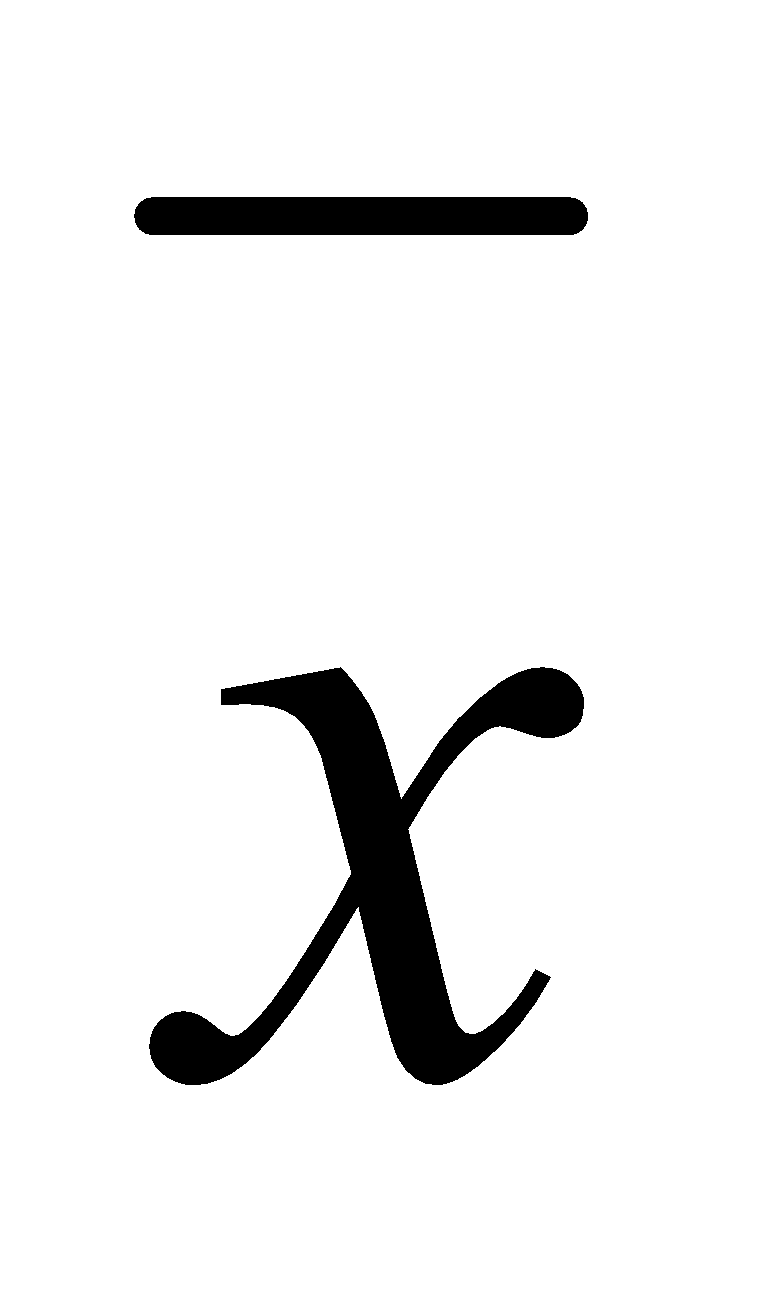= 12.5 min; σ = 5.65 min; CV = 0.45; Me =  11.92 min
  1. Calcula , σ y C.V. en la distribución dada en la tabla adjunta:
Intervalos
Frecuencias
200-240
57
240-280
82
280-320
73
320-360
31
360-400
15







Sol: 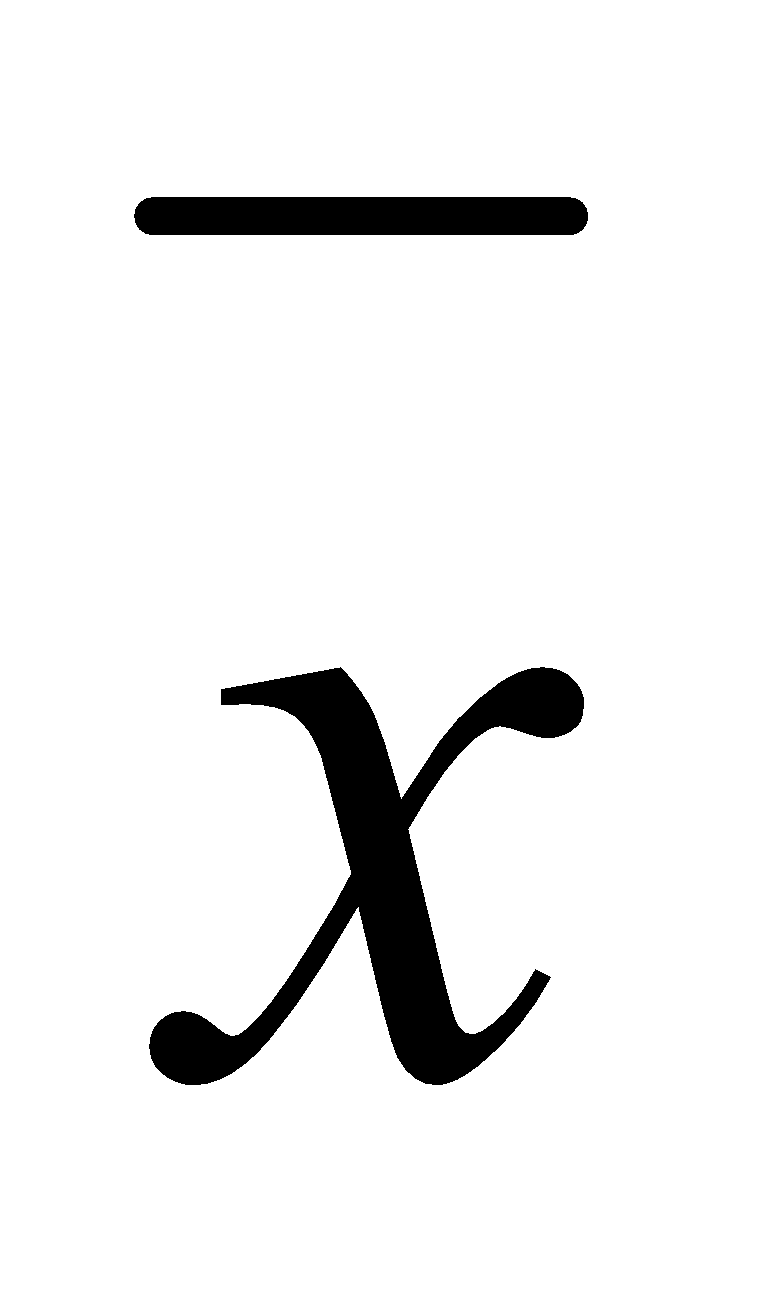= 279.069; σ = 45.2678; CV = 0.16 ; Me = 275.72

  1. Halla la media y desviación típica en el siguiente estudio:

A un grupo de 30 personas se les ha tomado el número de pulsaciones por minuto (ritmo cardíaco) obteniéndose los siguientes resultados:

87   85   61   51   64       75  80  70  69  82      80  79  82  74  90      
76   72   73  63   65       67  71   88  76  68      73  70  76  71  86   
  
Representa gráficamente la distribución.
¿Cuál es la variable? ¿De qué tipo es?
¿Qué porcentaje de datos se encuentra en el intervalo (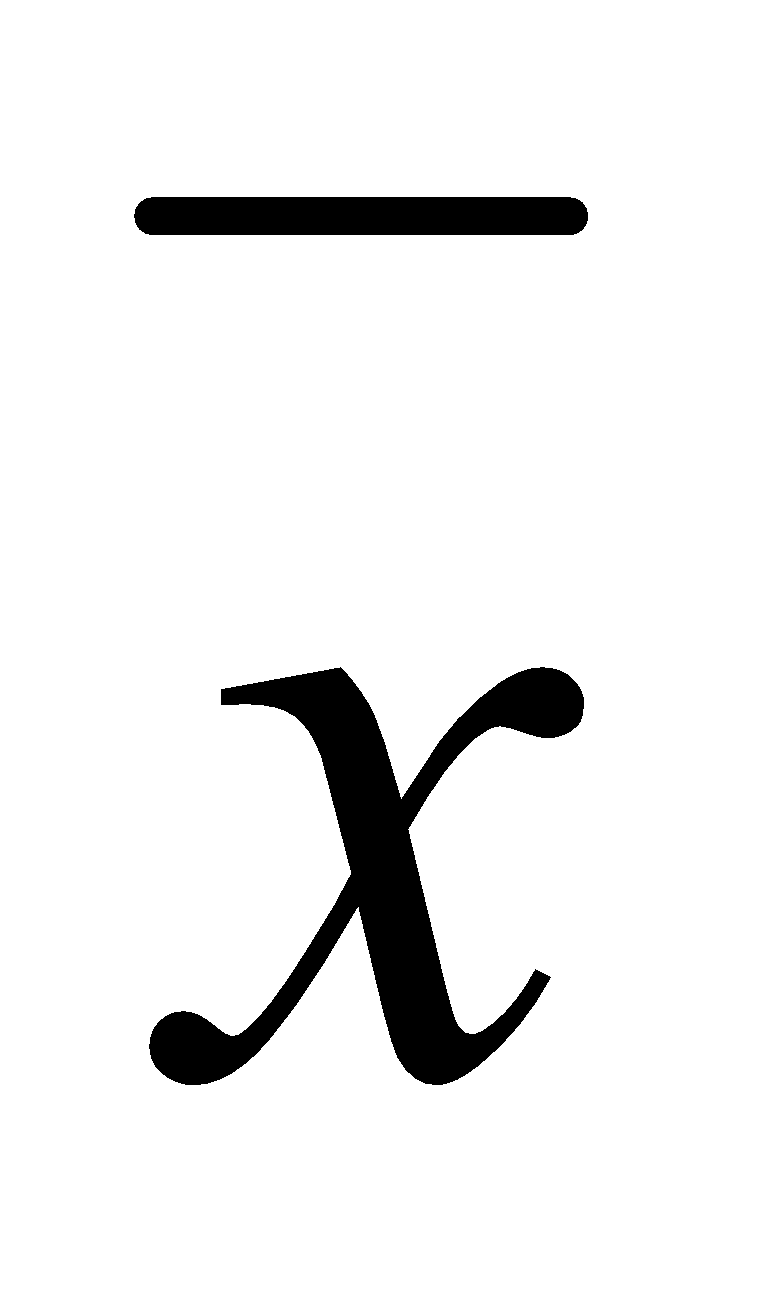-σ, 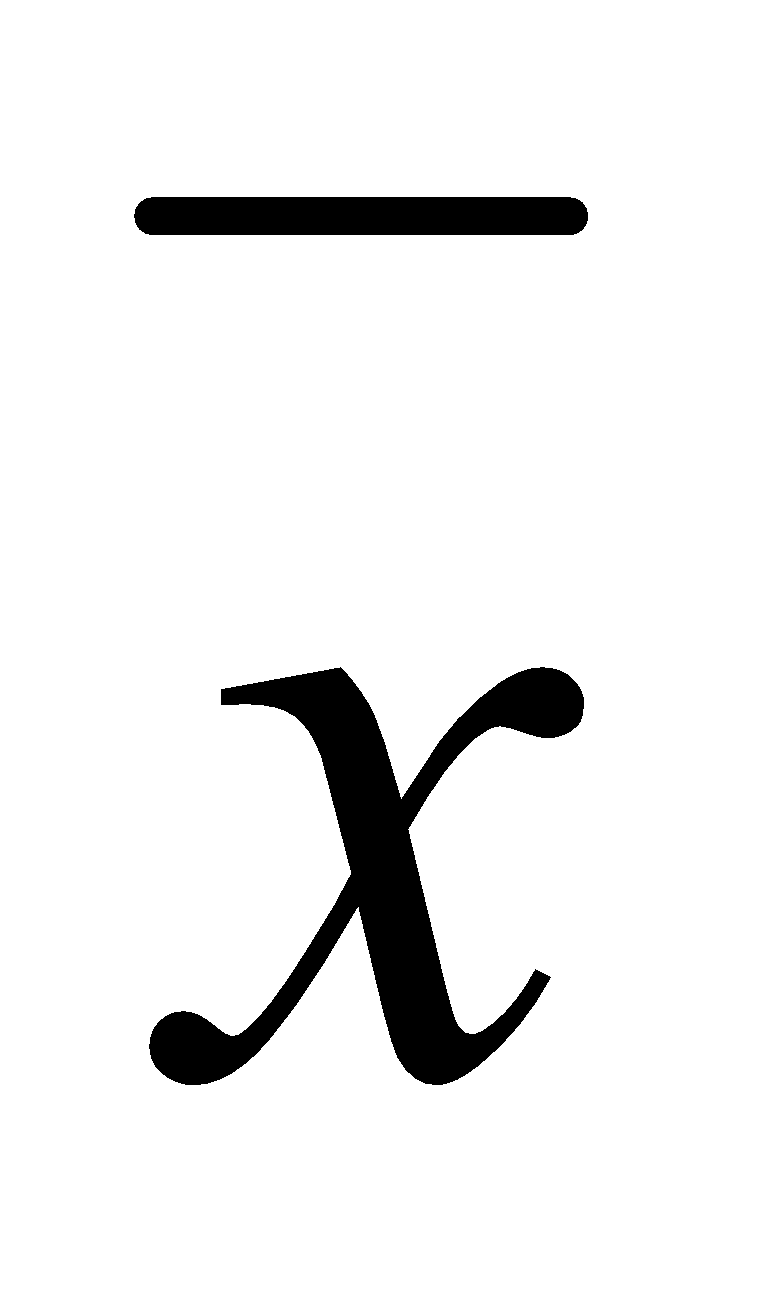+ σ) (Para ello, contar de los datos previos los individuos que están entre esos valores)












Sol: 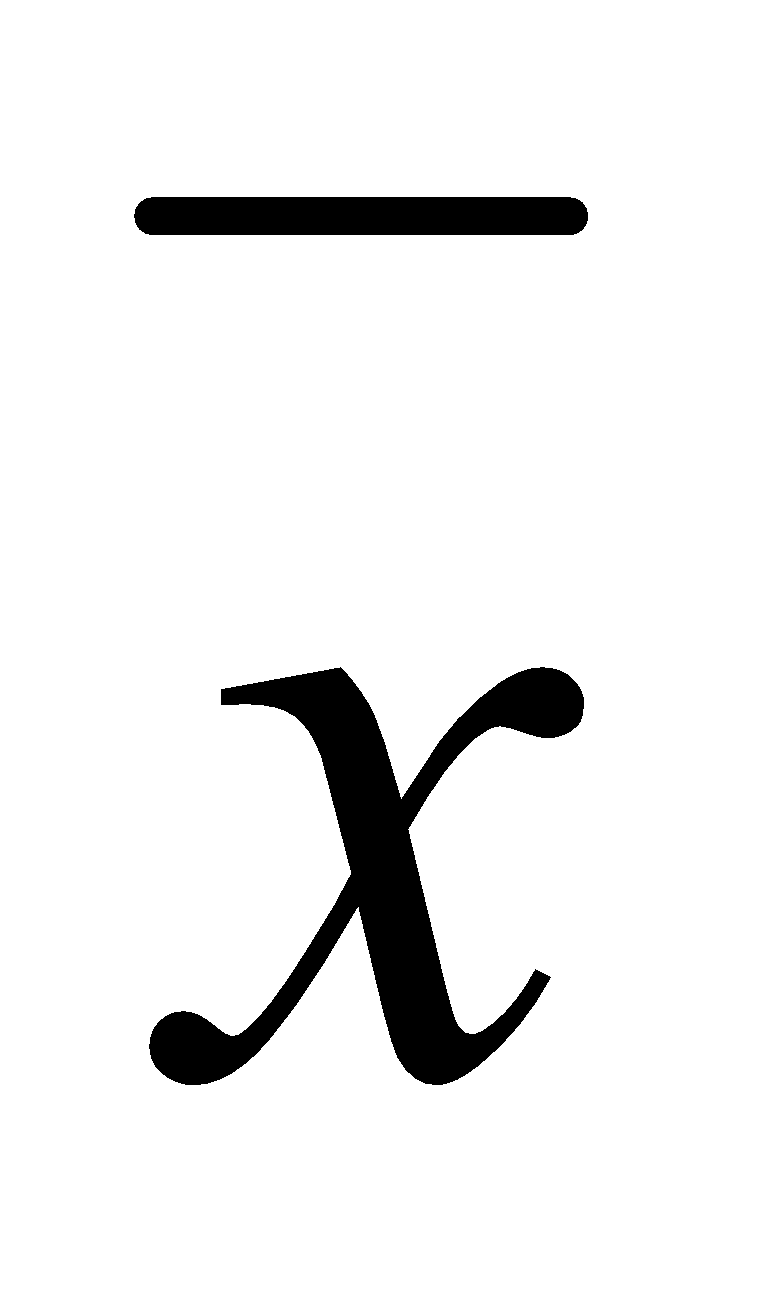= 74.8 pul/min; σ = 8.964puls/min; % = 65 %
  1. Se han medido los pesos y las alturas de 6 personas, obteniéndose los siguientes datos:

Pesos (kg)
Alturas (m)
65
1.7
60
1.5
63
1.7
63
1.7
68
1.75
68
1.8









Calcula la desviación típica de cada variable. ¿qué están más dispersos, los pesos o las alturas?  (para comparar la dispersión entre dos variables, comparamos los coeficientes de variación ya que ello nos da información más precisa).


       Sol: = 64.5kg; σp = 2.87kg;  = 1.69 m ; σh = 0.11 m. Las alturas están más dispersas que los pesos (C.Vh.> C.V.p  0.07>0.04)
  1. Esta tabla nos da la tasa de fecundidad (número de nacimientos por cada 1000 mujeres) según la edad, en un país europeo:
Edad (años)
Nº nacimientos
40
396
700
450
160
40








Halla la media, mediana, desviación típica y C.V.









Sol: Me= 28.26 años; = 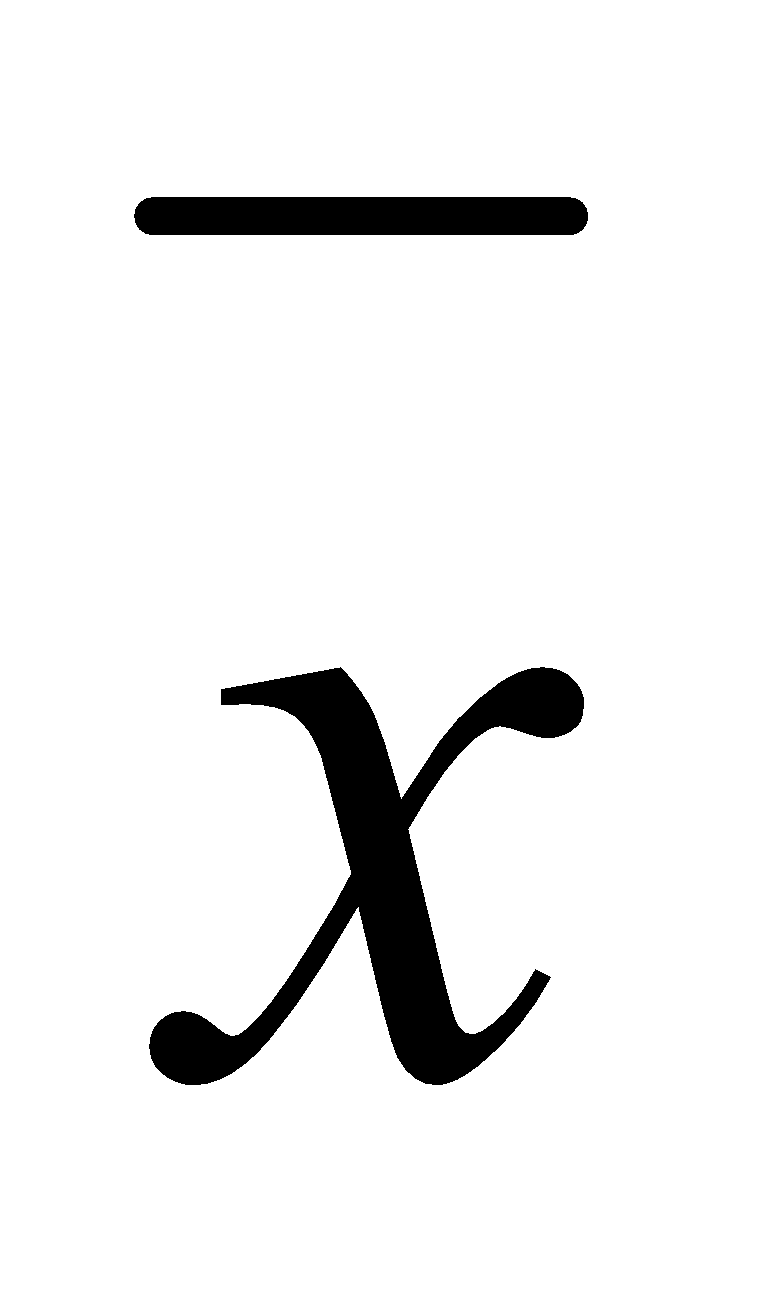= 28.71 años; σ = 5.36 años; CV = 0.18
  1. En una población de 25 familias se ha observado la variable X = “número de coches que tiene la familia” y se han obtenido los siguientes datos:
0
1
2
3
1
0
1
1
1
4
3
2
2
1
1
2
2
1
1
1
2
1
3
2
1
a) Construye la tabla de frecuencias de la distribución X.
b) Haz el diagrama de barras.
c) Calcula la media y la desviación típica.
d) Halla la mediana y la moda.














Sol: = 1.56 coches; =0.94 coches; C.V.= 0.6 ; Me = 1 coche ; Mo = 1 coche
  1. El número de faltas de ortografía que cometieron un grupo de estudiantes en un dictado fue:
0
3
1
2
0
2
1
3
0
4
0
1
1
4
3
5
3
2
4
1
5
0
2
1
0
0
0
0
2
1
2
1
0
0
3
0
5
3
2
1
a) Di cuál es la variable y de qué tipo es.
b) Haz una tabla de frecuencias y representa los datos en un diagrama adecuado( d. de sectores, “quesitos”. Cálculo del tamaño del sector: ).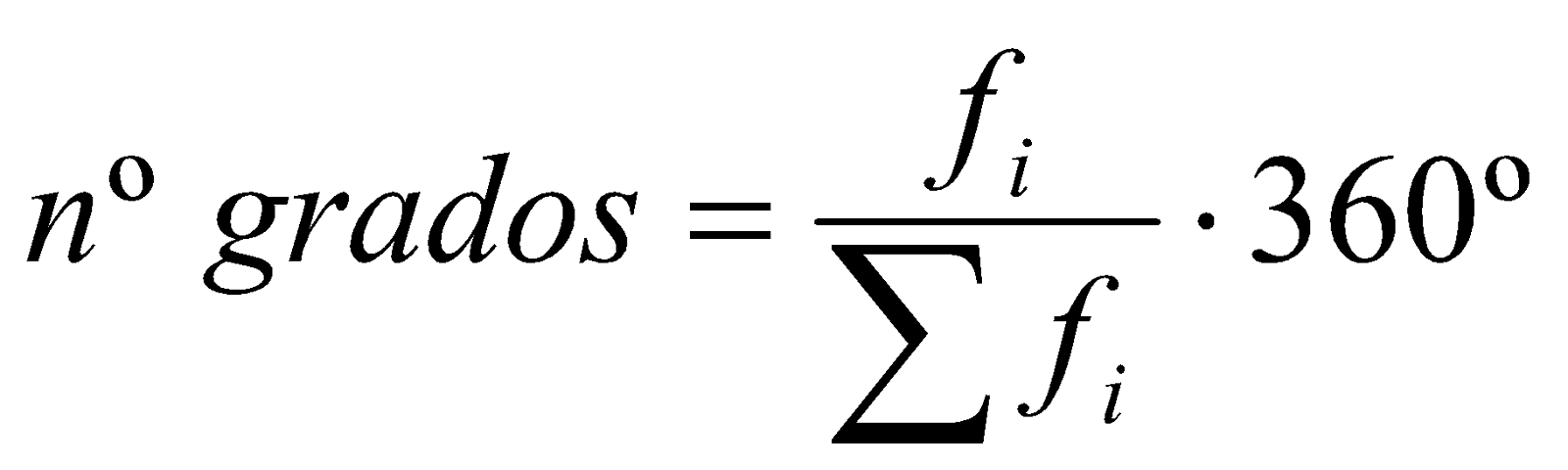
c) Calcula la media y la desviación típica, la mediana y la moda.






Sol: = 1.7 faltas ; =1.568 faltas; CV = 0.92 faltas; Mo = 0 faltas; Me = 1 falta
  1. En el proceso de fabricación de un vino, a este se le añade un compuesto químico:
Concentración (mg/l)
Nº de botellas
15
38
76
57
14
  1. Calcula la media, la desviación típica, la mediana y la moda.
  2. Se estima que el vino no se debes consumir si la concentración de ese compuesto es superior a 20.9 mg/l. Según esto, ¿Qué porcentaje de botellas no es adecuado para el consumo?













Sol: = 20.517 mg/l; = 0.20 mg/l; % = 3.5 %
  1. Se han realizado 50 lanzamientos con un dado, obteniendose los siguientes resultados:
Resultado
1
2
3
4
5
6
Nº de veces
6
10
5
7
10
12
Calcula la media, desviación típica, mediana y moda.
¿Qué porcentaje de resultados hay en el intervalo (-,  +)?









Sol: Me= 4; Mo= 6; = 3.82; = 1.76; % = 44%
  1. Se ha preguntado a un grupo de personas cuántas veces han ido al cine en el último mes. Estos han sido los resultados:
Nº veces cine
0
1
2
3
4
5
Nº personas
2
20
41
26
9
2
Calcula la media, desviación típica, mediana y moda.
¿Qué porcentaje de resultados hay en el intervalo (-,  +)?










Sol: Me = 2 veces; Mo = 2; = 2.26 v; = 1.00 v; % = 67%
  1. Hemos preguntado las edades a un grupo de personas y estas han sido las respuestas:
Edad
Nº personas
4
8
10
9
17
2
Calcula la media, desviación típica, mediana y moda.














Sol: Me = 16.6 años; = 15.8 años; = 6.95 años


Suscribirse a: Entradas (Atom)